这其实是我在2013年7月写的一篇博客文章。刚才看到一位长得很帅的师弟
在他的公众号里
提到了这个悖论,所以顺手推送一下旧文,供大家周末烧脑用。
§1.1
你被邀请参加这样一个游戏:
在你面前放着两个箱子。甲箱是
透明
的,里面有
M
美元;乙箱是
不透明
的,里面
要么
有
N
美元(
N
大于
M
),
要么
一分钱都没有
。
乙箱不管怎样都归你,但在邀请你来做客的主人于
t
1
时刻
揭晓乙箱内容
之前,你必须先在规定的
t
时刻
选择是否打开甲箱
:打开了,甲箱里的
M
美元就一并归你;不打开就没份。
在
t
之前的某个
t
0
时刻
,主人会根据他对你将如何选择的预判,来相应安排乙箱内容:
如果他认为你会在
t
时刻选择打开甲箱,就不往乙箱里放钱;如果他认为你会在
t
时刻放弃甲箱,就往乙箱里放
N
美元
。当然,你并不清楚主人的预测结果是什么,只知道
乙箱内容从
t
0
时刻确定之后就不再变动
。
已知
主人的预测神准
,在过去的无数次游戏中,无论玩家选择的是打开甲箱还是放弃甲箱,全都被他猜中,无一失手。
你到底该不该选择打开甲箱?
§1.2
从表面上看,这个悖论体现的是博弈论中“优势策略”与“预期效用”两大基本原理之间的冲突。
根据
优势策略
原理,不管最后乙箱里头究竟有没有钱,
你选择打开甲箱,总是能多得
M
美元
(可以用
Δ
来表示这个差额)。换言之,与“放弃甲箱”相比,“打开甲箱”永远是优势策略,所以应该选择打开甲箱。
|
打开甲箱
|
放弃甲箱
|
|
主人预测放弃甲箱(乙箱放钱)
|
M+N
|
N
|
|
主人预测打开甲箱(乙箱不放钱)
|
M
|
0
|
|
Δ
= M
>
0
|
但从
预期效用
的角度出发,结论却正好相反。主人的预测如此可靠,意味着他猜中你选择的概率为
1
,而猜错的概率为
0
。换言之,
如果你选择打开甲箱,乙箱就必然是空的,你只能拿到
M
美元;如果你选择放弃甲箱,就必然可以在乙箱里收获
N
美元
。显然,放弃甲箱才是明智之举。
|
打开甲箱
|
放弃甲箱
|
|
主人预测成功(概率
1
)
|
M
|
N
|
|
主人预测失败(概率
0
)
|
M+N
|
0
|
|
预期效用
|
M
|
N
|
|
Δ
= M–N
<
0
|
当然,“优势策略派”会对此加以反驳:不管主人过去预测的正确率有多高,都不能改变这样一个事实:
当你在
t
时刻做出选择时,乙箱里有没有钱是早已确定了的
,你打开甲箱,并不会让
t
0
时刻放进乙箱里的
N
美元凭空消失;放弃甲箱,也不会让空无一物的乙箱里突然变出钱来。在一切都已确定的情况下,什么过往记录、概率分析、预期效用,通通是无关紧要的。甲箱里的钱,不要白不要。
然而“预期效用派”也有话说:我们知道,主人的预测记录是完美的。过去那些遵循优势策略原理的玩家,最后都只拿到了
M
美元,而所有遵循预期效用原理的玩家,最后都得到了
N
美元。
你没有理由认为自己跟别的玩家有任何不同
。还是该向以前那些选择放弃甲箱的玩家看齐才对。
两派看起来都挺有道理的。怎么破?
§1.3
以上就是物理学家威廉·纽科姆提出的“纽科姆悖论”(
Newcomb's paradox
)。
悖论之所以成为悖论,无非两个原因,一是
提供的事实信息不够充分或相互冲突
(这两者实际上是一回事,因为信息相互冲突而不被察觉往往是因为我们尚未发现更基本的相关法则),二是
利用了日常语言中阐释性概念的模糊性
,从而使得相互冲突的直觉从表面上看都可以成立。
事实上,从“优势策略派”与“预期效用派”的争论中可以看出,纽科姆悖论的题目条件中首先缺失了这样一个关键信息:
主人完美的预测记录,背后依赖的原理到底是怎样的?
你在
t
时刻的选择,究竟能不能(在某种意义上)反过来影响主人在此前
t
0
时刻的预测,从而决定乙箱的内容?主人在过去的游戏中从未预测失败,究竟是因为他(因为某种特定的机制而)必然能够做出正确预测,抑或只是因为他(因为某种特定的机制而)有相当大的概率能够做出正确预测、并且恰好迄今尚未发生错误?
不知道这方面信息,就无法确定到底是该运用优势策略原理还是预期效用原理,也就无从给出相应的最佳策略。
§2.1
什么样的原理能够保证“主人的预测必然正确”?
一种可能是:主人是个类似于基督教上帝那样全知的神(“世上不存在神”这个事实并不妨碍我们做这样一个思想实验),在创世那一刻就已经精确预见到了未来每分每秒世界上将要发生的任何事情。让他预测你区区一个人类会不会在
t
时刻选择打开甲箱,自然不在话下。
面对能够预见一切的神祗,你显然应该果断选择放弃甲箱,好让他事先往乙箱里放钱,对吧?
§2.2
且慢。
假如真有这样一位全知神,在创世之初就预见了之后的所有一切大小事宜,那岂不是说,之后发生的所有一切(包括你的整个人生,当然更包括你在这个游戏中的所有思考和行动、包括你最后到底是会打开甲箱还是放弃甲箱)早在创世时就已经被决定好了?可是这样一来,“你到底该不该选择打开甲箱”岂不成了一个伪问题?——你的一举一动早就被全知神安排好了,哪里有任何让你“选择”的余地。你自以为在“选择”,其实只不过是全知神自导自演的独角戏中的一个傀儡道具罢了(《
上帝与罪恶问题
》)。
这就涉及到应当如何理解日常语言中“选择”这一(阐释性)概念的问题了。
(2.2.1)
这里很容易联想到康德四个二律背反里的第三个,以及自由意志问题上“相容论者”与“不相容论者”的争论:相容论者认为,即便在一个事事都已被预先决定了的世界里,我们仍然有理由认为自己拥有自由意志、拥有真正意义上的选择;而不相容论者认为,自由意志、真正意义上的选择,这些概念根本是与决定论的世界观是不相容的,只有把某种
非决定论的机制
(比如量子不确定性)引入对意志活动的解释,才得以可能。
于是纽科姆悖论“全知神情境”的解法就和你在相容论问题上的立场结合了起来:如果你自认为是一个
相容论者
,就该毫不犹豫地说:“
假如主人真是全知的神,我当然要选择放弃甲箱
。”如果你自认为是一个
不相容论者
,就该对这个问题嗤之以鼻:“
要是真有全知的神,那还选个屁啊
。”
(2.2.2)
这个联想是有一定道理,但是需要注意一点:
相容论本身只说自由意志与决定论的世界观相容,并没有说自由意志与全知神这样一种角色相容
。一个决定论的世界(由于混沌机制的存在)完全可能是
无法预测细节
的。不少相容论者认为,正是这种认识论层面上的细节不可预测性,保证了自由意志概念在决定论世界中的意义。而全知神的存在显然是与细节不可预测性相抵触的。因此如果你属于
这一类相容论
者,那么你仍然该说:“
要是真有全知的神,那还选个屁啊
。”
§3.1
科幻迷会说,并不是只有全知神的预测才必然正确,一个拥有时间机器的普通人同样可以做到这一点。假如主人拥有时间机器,他可以有许多种作弊的办法来保证自己能够“预测”得准确。考虑到所有这些作弊办法都
至少需要从
t
时刻之后“往回”向
t
0
时刻之前穿越一次
,可以将它们分为两类:
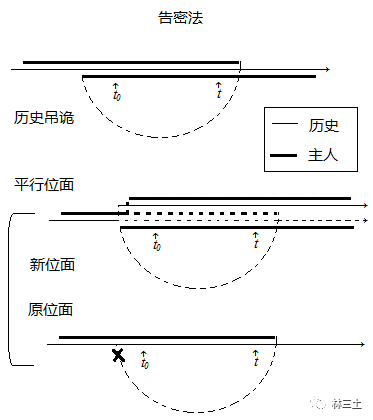
“告密法”
:由
t
时刻之后的某人(“未来的”主人或其助手)穿越回到
t
0
时刻之前,将你如何选择的信息带给即将“预测”的主人;
“偷窥法”
:先由
t
0
时刻之前的某人(“过去的”主人或其助手)穿越前往
t
前后的某个时刻,在获取了你如何选择的信息之后,再将其“亲自”带回
t
0
时刻之前。
这样一来,似乎既保证了主人的“预测”必然正确,又避免了“全知神情境”所导致的决定论难题——你不必怀疑题目有没有意义,安心选择放弃甲箱就好。
然而事实上,
单从“主人拥有时间机器”出发,并不能马上推出“主人的‘预测’必然正确”
。我们仍然需要知道关于时间穿梭(或者说关于这个允许时间穿梭可能性的世界)的更详细设定,以及其它相关的信息。
这里所谓“设定”,指的是
与时间穿梭密切相关的一整套自然法则或物理法则
,只是我们目前(因为尚未实现时间穿梭)并不知道这些法则的具体内容,只能做出一定假设;一肆时间穿梭的原理被发现,这些法则的内容很自然地也将为我们了解。当然,这一切都是建立在假设时间穿梭可能的基础上的。
§3.2
首先需要问的是:根据设定的物理法则,
穿越回到过去的做法会对既有历史造成什么影响
。
之所以有这个问题,是因为严格地说,穿越回到过去是无法“改变”既有历史的。因为倘若既有历史可以被“改变”,就会出现类似于
“祖父悖论”
的一系列逻辑矛盾:假设一个人穿越回到他祖父还是婴儿的时候,把后者给杀了;既然穿越者的祖父死了,世界上就从来不曾有过穿越者本人存在;既然穿越者不存在,就没有人回到过去杀死那个婴儿;既然婴儿没死,若干年后穿越者又会按既有历史出生,并在长大后穿越回去杀死他的祖父……
由于穿越前任一时刻的世界整体状态都和穿越瞬间的世界整体状态具有因果联系,只要容许了“改变”历史的可能性,便牵一发而动全身,导致逻辑的全盘崩溃。
(3.2.1)
诚然,绝大多数涉及时间穿梭情节的文艺作品都声称穿越回到过去的人物“改变”了(或者有可能“改变”)历史,比如电影《回到未来》、《蝴蝶效应》,以及如今泛滥网络的从汉穿唐穿宋穿到明穿清穿民国穿的各种穿越小说。
但事实上,这些穿越者所做的
并不是“改变”历史,而是触发历史的分岔
。在这类设定中,任何一次回到过去的穿越,都会在落脚点上引起扰动,生成两个平行世界(或者说位面),其中一个沿着历史“原本”的轨迹运行,另一个则将拥有“全新”的历史(前往未来的穿越是否会生成平行位面,则需要进一步设定)。试图杀死祖父的穿越者到达过去的那一瞬间,出现了两个平行的位面:
“原位面”
中,这个瞬间并没有什么穿越者抵达,婴儿顺利成长,若干年后穿越者出生,长大后驾驶着时间机器消失;
“新位面”
中,穿越者到达,杀死婴儿之后留在这个位面中继续生活,而那个“若干年后的穿越者”则从来不曾存在过。换句话说,
穿越者并不是“从某年某月某日穿越回到若干年前”,而是“从某年某月某日的某个位面穿越到了若干年前的另一个位面”
。
以上便是绝大多数涉及时间穿梭的文艺作品都(要么明白无误地、要么不明所以地)采用了
“平行位面”设定
。
(3.2.2)
与此相对的是
“历史吊诡”设定
:在以海因莱因的著名短篇科幻小说《你们这些还魂尸》、日本喜剧电影《夏日时间机器蓝调》等等为代表的另一些作品中,时间穿梭并不对历史造成任何扰动、不生成任何平行位面;恰恰相反,
回到过去是这个(唯一的)位面中的既有历史获得“实现”的必要条件
。
根据这种设定,试图杀死祖父的穿越者回到过去之后,在执行计划时必然会遭遇各种莫名其妙的挫折,导致任务失败(这些挫败全都是历史中“已经”发生过的,只不过穿越者自己并不晓得细节而已)。甚至还有可能出现类似这样的情况:穿越者因为操作机器失误,落脚点比预计的早了十个月,紧接着他跟一个姑娘发生了一夜情,姑娘怀孕生下了他的骨肉,结果这个婴儿正是他自己的祖父。总之,穿越者费尽心机,最后却只是验证了“历史的吊诡”。
§3.3
“历史吊诡”设定
需要对穿越的细节做出环环相扣的描述。以
“告密法”
为例:主人可以在
t
时刻(你宣布最终选择)与
t
1
时刻(揭晓乙箱内容)之间,借口上厕所(当然安排好了防止你偷看乙箱内容的措施),偷偷启动藏在厕所里的时间机器,穿越到
t
0
之前的某个时刻,把你的选择告诉尚未往乙箱里放东西的“过去的主人”。接着这位“未来的主人”就躲进厕所,直到“过去的主人”在
t
与
t
1
之间躲进厕所、启动时间机器消失之后,再“接班”走出厕所、揭晓乙箱内容。
显然,这种设定下主人的“预测”确实是
必然正确
的,所以至少从表面上看,你应该选择放弃甲箱。只是仍然需要考虑:
这种设定会不会和“全知神情境”类似,与自由意志的相容性问题存在密切关联、引发关于“在这种设定下你的‘选择’是否仅仅是一种幻觉”的争议
。
(3.3.1)
若是单从“‘历史吊诡’设定下的时间穿梭与‘全知神情境’在多大程度上类似”这个问题上说,确有一些哲学家把神的全知与时间穿梭相提并论,理由是两者都会涉及
逆向因果关系
。另一些哲学家则认为逆向因果关系是对“神的全知”的错误描述:严格说来,这里的因果关系应该是“神在创世时做出了‘未来某时刻将发生某事’的预见,而这将导致未来某时刻发生某事”,而不是“某时刻发生了某事,而这将(或者说已经)导致神在创世时做出‘未来某时刻将发生某事’的预见”。
但我们可以不去管这个争议,因为逆向因果关系与这里要考虑的“虚幻选择”问题并不直接相关。前面提到,“全知神情境”之所以会引发“虚幻选择”的担忧,有两层直接原因,一是
未来任一时刻的世界整体状态早在创世时就被决定好了
(这意味着
量子不确定性
实际上是派生于隐变量之类的伪不确定性),二是
神在创世时精确地预见了未来任一时刻世界整体状态中的任何细节
(对神的洞察力而言不存在
混沌
这样妨碍预测的机制)。
乍看起来,“历史吊诡”设定下的时间穿梭也存在这两个层面的困扰。
(3.3.2)
前一个层面的困扰:穿越出发点与落脚点之间的事件必须构成一个完整而自足的“因果链条圈”,圈内的事件都是“早已”决定好、无论历史再发生几次都不会改变的。而“你做出某个特定的‘选择’”作为这个圈里的一个事件,自然也是“早已”决定好、无论历史再发生几次都不会改变的。似乎世界至少在这个因果链条圈里是决定论的。
以
“告密法”
情境为例。假如在穿越落脚点与出发点之间的某个瞬间,厕所里藏着的时间机器旁边发生了一次奇怪的量子随机事件,并被一直躲在旁边的“未来的主人”与找借口进来准备驾驶机器的“过去的主人”同时观察到。如果我们
沿着主人“个人史”的时间轴看
,会觉得这个量子事件在他的生命中发生了两次,“第一次”是他进来准备驾驶机器的时候,“第二次”是他躲在厕所里等的时候。
而这个量子事件“第二次”发生时就不再是随机的了,因为它的过程与结果必须和“第一次”一模一样。但如果“第二次”不是随机的,那么“第一次”应该也不是随机的,因为两者在“世界史”的时间轴其实是同一事件
。换句话说,因果链条圈里不可能存在真正的量子不确定事件。
但是如果
沿着“世界史”的时间轴来看
,历史并没有、也不可能“再发生几次”。
历史只发生过一次,也只能发生一次
。我们可以把主人的“个人史”时间轴理解为:
主人在唯一位面唯一历史的不同人物角色之间发生穿越
(对比一下“平行位面”设定中,主人在不同位面之间穿越)。
在穿越的落脚点之前,世界上只有“过去的主人”这个人物;在落脚点与出发点之间,世界上同时存在“过去的主人”与“未来的主人”两个人物;在出发点之后,只有“未来的主人”这个人物,而“过去的主人”则在世界上从此消失。主人进行时间穿梭,只不过是从“过去的主人”这个人物角色穿越到若干时间以前在世界上凭空出现的“未来的主人”这个人物角色,然后把接下来“已经发生”的历史从不同的人物视角重新观察体验一遍而已
,就好像你对着摄像机镜头自拍完一段视频之后,打开文件以观众的视角审视自己刚才的表演一样。视频里录下的一切并没有因为你的播放而“再发生一次”;同样,主人的穿越并没有使得他看到的量子事件“(不随机地)再发生一次”。在时间穿梭造成的因果链条圈里,量子不确定事件仍然是真正的不确定事件。
(3.3.3)
另一个层面的困扰:主人通过穿越关于把你如何选择的细节信息带回过去,使得“过去的主人”做出一个必然正确的“预测”,似乎和神的全知一样违背了
认识论层面的细节不可预测性
?
这里关键在于,与“全知神”预先洞察任意时刻世界整体状态的所有细节不同,主人带回的只是
一个相当局部的细节
。而且他也只能带回一个相当局部的细节。比如他根本无法观察到你在做出选择之前的整个思考过程,以及这个思考过程所对应的大脑中复杂的分子运动。
“毫不犹豫地选择打开甲箱”和“经过一番激烈的内心斗争后选择打开甲箱”,对一旁观察的主人来说,信息量是相同的,但是对于(作为一个相容论者并且关心细节可预测性问题的)你的“自由意志”而言则大有区别
。
所以结论是,与“全知神情境”不同,在
“历史吊诡”设定
下的“时间机器情境”中,纽科姆悖论并不是伪问题,并且你
应该选择放弃甲箱
。
§4.1
反观
“平行位面”设定
,由于每次穿越回到过去都会在原有历史之外引出一条新的时间线,因此对穿越细节的描述不必如“历史吊诡”设定下那样苛刻。但正因如此,其因果效应也更为复杂。
(4.1.1)
假设在你这一轮游戏中,主人本人采用
“告密法”
,从
t
时刻之后“往回”向
t
0
时刻之前穿越一次,那么在他的穿越落脚点上(
t
0
之前的某个时刻)将生成两个平行位面,“原位面”与“新位面”:
在“新位面”上,主人顺利抵达过去,并向“过去的主人”传递了你在“原位面”的
t
时刻“将会”如何选择的信息。
严格地说,既然这个位面上
t
0
之后的历史已经与“原位面”不同,就无法从逻辑上确保你即将在“新位面”上做出的选择仍会与“原来”一模一样。不过考虑到
对因果链的扰动效应需要充分的时间来扩散
,主人完全可以通过各种措施(包括避免让你看见“两个”主人同时出现)来防止其穿越的扰动效应在
t
0
到
t
的时段里影响到你的选择,而且
主人过去完美的预测记录也表明这种扰动的概率微乎其微
,因此就实际效果而言,可以认为主人所传递的信息等同于你在“新位面”
t
时刻将会做出的选择。
显然,这种情况下应该放弃甲箱才对。
而在“原位面”上,这个时间点并没有什么“未来的主人”抵达,“过去的主人”由于没有得到来自未来的信息,因此仅就“预测”能力而言,跟一个没有时间机器的普通的理性人毫无区别
。
在这个位面上,“优势策略派”的思路便适用了。
注意
“原位面”的情况与真正的“普通的理性人预测”情境仍然有些不同
:如果预测者和你一样完完全全是个普通的理性人、并且相互都知道这一点,那么他就能够断定你必然会根据优势策略原理选择打开甲箱,而他也会相应地必然不往乙箱里放钱;而在目前这种情况下,由于
“原位面”上的主人知道你并不知道你自己究竟是处于“原位面”还是“新位面”
(因为他这一次“开始作弊”要等到
t
时刻你做出选择之后,而“新位面”
t
0
到
t
的时段里针对你的扰动得到了有效控制,所以
至少到目前为止两个位面对你而言没有可以分辨的差别
),因此在缺乏更多信息的情况下,他无法断定作为理性人的你必然会根据优势策略原理选择打开甲箱。但是无论如何,“原位面”上的
Δ
总是
M
美元。
好吧,你不知道自己究竟是处于“原位面”还是“新位面”。不过一个很自然的假设似乎是:两个位面在生成上并没有性质的差异,因此
你身处两个位面的概率是相等的
。
|
[
告密法
]
|
打开甲箱
|
放弃甲箱
|
Δ
|
|
主人成功回到过去(概率
1/2
)
|
M
|
N
|
M – N
|
|
主人穿越失败
(概率
1/2
)
|
猜你打开甲箱
|
M
|
0
|
M
|
|
猜你放弃甲箱
|
M+N
|
N
|
|
Δ
= M – N/2
|
这样得到的结论似乎是,当主人本人采用
“告密法”
时,只要
M/N
>
1/2
,你就应当选择打开甲箱;若
M/N
<
1/2
,就选择放弃甲箱。反过来,又可以知道在
“原位面”
中,当
M/N
>
1/2
时,主人必然不会往乙箱里放钱;而当
M/N
<
1/2
时,主人必然会往乙箱里放钱。
(4.1.2)
不过且慢。需要注意的是,以上关于“告密法”的结论其实依赖于这样的前提:
必须由主人“本尊”亲自进行时间穿梭,而不能由助手或者其“分身”代劳
。
不能由助手代劳很容易理解。倘非如此,主人就可以
在同一轮游戏中无限次地作弊
:只要发现自己预测失败,就派出一名助手往回穿越一次,“改变”一下历史。这样一来
对你而言,“主人预测能力与普通人无异”的概率(也就是你身处一个历史完全不受“改变”的位面的概率)便衰减为零了
。
而
由主人本人出马的话,穿越回去的他将不会出现在“原位面”中
。假如这是主人第一次进行时间穿越,那么在“原位面”穿越出发点(
t
之后的某个时刻)之后的历史中,世界上将不再有主人这个人物存在,再次作弊也就无从谈起。
但我们又知道
这并非主人第一次穿越
。恰恰相反,主人此前已经进行过无数轮游戏,并且按照你身处的这个位面(或者说这两个位面)的既往历史,主人的预测记录完美无瑕,这意味着他在这段历史中的已有穿越都是成功的。根据“平行位面”设定,每次成功地向过去穿越,都会让“新位面”在“过去的主人”之外多出一位“未来的主人”;由于“过去的主人”并不像“历史吊诡”设定下必须要穿越回过去,因此
新的历史中,世界上从今往后就要平白多出一个主人的“分身”来。主人之前已经无数次成功地往回穿越,意味着世界上已经有了无数个主人的“分身”。这样一来,主人又可以利用这些“分身”(就像利用助手一样),在同一轮游戏中无限次地作弊了
。
显然,
如果允许助手或主人的“分身”通过时间穿梭帮助作弊的话,主人的预测失败的可能性便可以忽略不计了
。这种情况下,你毫无疑问应该
选择放弃乙箱
。
(4.1.3)
但是引入助手或“分身”的存在,反过来又会给主人造成许多实际的麻烦。比如一个很棘手的问题是:无数次的成功穿越使得这个世界上有了无数个主人的“分身”(或者助手的“分身”),
且不论世界上塞不塞得下他们,单说主人平时如何负责这些人的衣食住行、如何不让别人发现他们的存在而产生疑心?
在电影《致命魔术》中,主人公之一为了魔术效果不断(通过与时间穿梭不同的另一种方法)制造分身又
杀死分身
,在地下室中一整列一整列地储存着“自己”的尸体。或许在你受邀参加的这个游戏中,主人也同样要“处理”掉之前无数次时间穿梭产生的“分身”呢(比如每次“未来的主人”穿越回到过去后,都要立即暗中杀死“过去的主人”,取而代之进行“预测”),所以你自打踏进他的家门后,才会一直没有见到他的任何“分身”的存在。
鉴于诸如此类的麻烦,
尽管利用助手或“分身”实现针对同一轮游戏的无限次作弊最能帮助主人提高“预测”的正确率,但主人仍有很大的可能不采取这种策略
,而倘若你从头到尾没有见到长相与主人一模一样的人(或者相互之间长得一模一样的管家、保安、侍从之类人物)出现的话,也能够间接印证这一点。
因此考虑这个问题仍然是有意义的:
倘若在这场游戏中,除了被邀请的玩家(比如你)之外,主人的“本尊”是唯一的参与者,同时也是唯一的穿越者,那么,你应该采取怎样的策略?
§4.2
前面提到,在
“平行位面”设定
下,倘若除玩家之外由且仅由主人“本尊”参与游戏及穿越,那么在你
确知
主人本次(将会)采用
“告密法”
作弊的情况下,你的选择策略取决于
M/N
和
1/2
的大小关系
。
但是除了极特殊的情况(比如你根据超前的物理知识发现,只有回到过去的穿越才是可能的,前往未来的穿越不可能)之外,
你并不知道主人这次具体(将会)怎么使用这台时间机器
。要找出一般性的策略,只能姑且假设本次游戏中,由“未来的主人”把未来的信息传递回过去的策略(
“告密法”
)被使用的概率为
q
,而由“过去的主人”前往未来窃取信息再回到过去的策略(
“偷窥法”
)被使用的概率为
1–
q
。
(4.2.1)
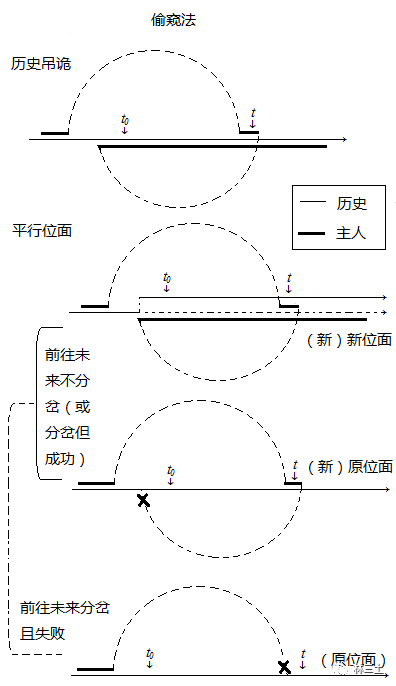
在
“偷窥法”
中,主人需要两次动用时间机器。第二次是从
t
之后往回赶到
t
0
之前,根据前面的讨论,这种往回的穿越必然在落脚点上引出两个平行位面。第一次使用时间机器则是从
t
0
之前的某个时刻往未来穿梭,“平行位面”设定本身并没有规定这类穿越会不会生成平行位面,所以这里还需要引入
关于“前往未来是否生成平行位面”的额外设定
才行:
假如前往未来的穿越不会生成平行位面
,那么你有
1/2
的概率
身处“主人顺利回到第一次穿越的出发点并做出必然正确的‘预测’”的
“新位面”
上,选择打开甲箱将获得
M
美元,放弃甲箱则获得
N
美元;
假如任何时间穿梭都会生成平行位面
,那么你只有
1/4
的概率
身处结果与此相同的
“‘新’新位面”
上。
需要注意的是,如果主人
未能顺利回到穿越出发点
,那就不单单是无法做出正确“预测”的问题了,而是会出现这样的结果:
由于他没能赶回来往乙箱里放东西,因此乙箱里必然是空的
。这种情况下你选择打开甲箱将获得
M
美元,放弃甲箱则分文不得。
(4.2.2)
乍看起来,“偷窥法”比“告密法”多涉及的一次时间穿梭不但叠床架屋毫无必要,而且在“任何时间穿梭都会生成平行位面”的设定下还平白增加了“主人未能成功穿越”的位面数量,有百害而无一利,主人只要有理性的话,应该根本不会选择这种策略才对?
两方面原因。
一方面,这里所谓主人穿越的“成功”或“失败”,与时间机器爆炸之类真正意义上的“事故”不同,只是从
旁观者的视角
(或者说“世界史”的时间轴),来描述时间穿梭在不同位面中对历史的影响而已。倘若从
主人本身的视角
(或者说穿越者“个人史”的时间轴)来看,
一旦他顺利穿越到“新位面”之后,“原位面”上此后发生的一切(包括“主人这个人物从此在世界上消失”)便与他无关了
。多穿越几次,对主人本身并不造成任何伤害。
另一方面,操作得当的话,使用“偷窥法”可以
避免前面那种靠不断杀死“分身”来解决“无穷分身”问题的做法
。由于并不像“告密法”那样要求“未来的主人”与“过去的主人”有直接接触,因此在“偷窥法”中,回到
t
0
之前的“第二次穿越后的主人”可以小心地避免这次穿越的因果扰动效应扩散到前往
t
前后的“第一次穿越后的主人”身上,以保证其能够顺利地完成第二次穿越。如此一来,在第一次穿越的出发点之后,世界上又将只剩下一个“主人”。如果主人在杀害“分身”问题上比较纠结的话,“偷窥法”会是一个不错的选项。
(4.2.3)
问题是
你如何判断,自己身处的位面中,主人是否成功带回了未来的信息?
如果你
在
t
0
到
t
之间见过主人
(比如当你做选择时主人就在现场),那就表明你所处的位面中,至少他的第一次穿越是成功的(否则的话主人将在
t
0
之后从这个世界上彻底消失),但你仍然不知道他的第二次穿越是否成功(因为只要主人完全可以把第一次穿越的落脚点选择在
t
之前),只能假设两种情况几率相等。
但是就算主人顺利回到回到位面上,也有可能躲起来不见你(并且早在游戏开始前就做好了安排,让你在
t
时刻进行选择时不必等他在场)。这时就需要依赖前面所说的进一步设定了:假如前往未来的穿越不会生成平行位面,那么你有
1/2
的概率处在“新位面”上;假如任何时间穿梭都会生成平行位面,那么你有
1/4
的概率处在“‘新’新位面”上。
|
[
偷窥法
]
|
打开甲箱
|
放弃甲箱
|
Δ
|
|
主人穿越成功
|
M
|
N
|
M – N
|
|
主人穿越失败(无法往乙箱放钱)
|
M
|
0
|
M
|
|
预期效用
|
t
0
至
t
之间主人出现
或前往未来不生成平行位面
(穿越成功的概率为
1/2
)
|
M
|
N/2
|
M – N/2
|
|
t
0
至
t
之间主人未出现
且任何时间穿梭均生成平行位面
(穿越成功的概率为
1/4
)
|
M
|
N/4
|
M – N/4
|
(4.2.4)
把这个结果和前面对“告密法”和“偷窥法”的分析综合起来,可以知道,在
“除玩家之外由且仅由主人‘本尊’参与游戏及穿越”
的情况下:
若
t
0
至
t
之间主人出现
、
或者
只有回到过去的穿越才会生成平行位面
,那么是否选择打开甲箱依赖于
M/N
与
1/2
的大小关系
。
|
Δ
|
|
告密法(概率为
q
)
|
M – N/2
|
|
偷窥法(概率为
1–
q
)
|
M – N/2
|
|
预期效用
|
M – N/2
|
|
若
M/N
>
1/2
,打开甲箱
若
M/N
<
1/2
,放弃甲箱
|
若
t
0
至
t
之间主人未出现
、
并且
任何时间穿梭都会生成平行位面
,那么是否选择打开甲箱依赖于
M/N
与
(1+
q
)/4
的大小关系
,其中
q
是主人在本轮游戏中使用“告密法”而非“偷窥法”的概率。
|
Δ
|
|
告密法(概率为
q
)
|
M – N/2
|
|
偷窥法(概率为
1–
q
)
|
M – N/4
|
|
预期效用
|
M – (1+
q
)N/4
|
|
若
M/N
>
(1+
q
)/4
,打开甲箱
若
M/N
<
(1+
q
)/4
,放弃甲箱
|
§4.3
可以用下面这张表来展示“时间机器情境”中玩家应对策略的复杂性:
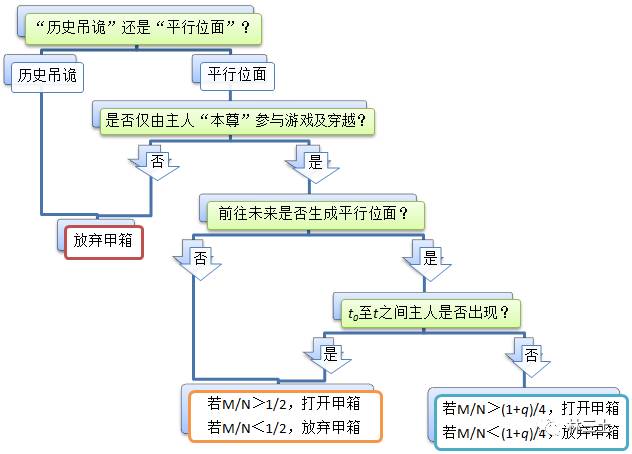
§5.1
无论是“全知神情境”还是“时间机器情境”,都是从
“主人的预测必然正确”
这个规定衍生出来的(当然,在讨论中我们也发现,某些时候拥有时间机器并不能推出主人的预测必然正确)。
现在让我们丢掉幻想,回到既没有神、也(暂时还)没有时间机器的
现实世界
。在这个世界中,主人的预测不可能是“必然正确”的,只能是
“有相当大概率正确(并且迄今尚未出错)”
。这时候你是该听取“优势策略派”的建议选择打开甲箱,还是该听取“预期效用派”的建议选择放弃甲箱?
§5.2
还是要先问:怎样的预测原理满足“有相当大概率正确”的条件?
一种可能是,主人是个
心理高手
。他邀请你来做客,在你玩游戏之前跟你聊天吃饭,观察你的言谈举止,揣摩你的性格特征,结合理论与经验准确预判出你将会采纳的游戏思路。他甚至可能会根据你的性格特点给你设下相应的思维圈套,诱导你做出特定的选择。由于他的手法非常高明,因此在过去的游戏中无往而不胜,玩家们被他卖了还帮他数钱(你会问说咦他不明明是想着法子白送钱给玩家么。我们不妨假设说主人其实在下很大一盘棋,比如他跟某个闲得无聊的大亨打赌自己心理战的功力,赌注级别远远超出你的想象,送你这点小钱他根本眼睛都不带眨的)。
(5.2.1)
知道主人是靠细致入微的心理观察(或诱导)来预测之后,你准备如何应对?仅仅在“一根筋地选择打开甲箱”与“一根筋地选择放弃甲箱”这两种策略之间比较的话,自然是后者为上;但是既然主人也有可能犯错(虽然之前运气好还没有犯过),你有没有办法利用这种可能性获利?换句话说,如果你可以做到
让主人误以为你将会选择放弃甲箱、而实际上你最终选择的却是打开甲箱
的话,这将是比“一根筋地选择放弃甲箱”更优的策略。
怎么做到这一点?最容易想到的办法,当然是以其人之道还治其人之身,跟主人搞心理战,通过有意识的
伪装
引他上当:
“哼,就让他放马来试探我吧,我步步留心时时在意,韬光养晦扮猪吃老虎,一半是海水一半是火焰,总之让他以为我会乖乖地选择放弃甲箱,直到我最后把甲箱打开时才大吃一惊大势已去大败亏输大彻大悟。哦,当然,之前那些玩家里肯定也有人打过这个主意,但是都被他看穿了,结果是画虎不成反类犬,赔了夫人又折兵。那很正常,毕竟他也算是个高手嘛,而那些玩家——嗤,不过是些不知道自己几斤几两只配领盒饭的战五渣罢了。而我,我这样风华绝代的人生温拿,自然和那些卢瑟们不能同日而语。”
(5.2.2)
很显然,你的策略是否能够成功,取决于你是不是妄自尊大、你对各方(你与主人、你与其他玩家)心理战实力对比的判断是否正确。
如果你其实不过是自以为是的战五渣一枚,遇到心理高手只有被玩得团团转的份,那还是别在这上头枉费心思了,
乖乖把甲箱放弃掉
吧,
N
美元已经够你乐的了。
如果你跟江湖传奇人物小白龙韦香主一样有胆有识霸气侧漏,如果主人
识破你伪装的概率
p*
<
(M
+
N)/2N
,那就请让我们欣赏二位的斗智斗勇罢。














