
►蒂莫西·高尔斯(Timothy Gowers),来源:美国数学协会
编者按:
蒂莫西·高尔斯(Timothy Gowers)是当今著名的数学家,1998年摘得数学界的桂冠菲尔兹奖,执掌剑桥大学的Rouse Ball教席。除了在纯数学领域的杰出成就之外,他还参与到了数学教育中。他所执掌的两本通俗数学读物的中文版都已面世,而他主编的 《普林斯顿数学指南》(The Princeton Companion to Mathematics)[1],涵盖了相当多的数学课题,以精炼的语言涉及了极大的广度,是一本全面的现代数学概览参考。由于其上千页的厚度,他在个人网页上风趣地将其戏称为《数学:极厚导论》(Mathematics: A Very Long Introduction)。
而与之相对应的是他更早先的仅有一百余页的小开本作品《数学:极简导论》(Mathematics: A Very Short Introduction)[2],更专注于深度而非广度,属于牛津大学出版社的极简导论系列[3],也是这次我们要讨论的书。
撰文 | 宋础良(麻省理工学院土木与环境系在读博士生)
责编 | 吕浩然
● ● ●
数学是人类最古老也是最完善的学科,要在一本小册子里向大众介绍数学并非易事。国内最为知名的数学科普书恐怕是Richard Courant的《什么是数学》(What Is Mathematics),但其四五百页的厚度和大量的公式估计会吓到一片。再比如胡作玄先生的《数学是什么》,页数也是将近四百页,除去这些科普书本身的厚度之外,其阅读门槛至少是我国高中数学大纲以上。更重要的是,这两本书的选材不是真正可以改变普通人对这个世界的认识的数学。在详细讨论高尔斯的书《数学:极简导论》之前,首先来审视一本合格的数学书需要满足什么条件。

►蒂莫西·高尔斯所著《数学:极简导论》
撰写面向大众的数学科普书是困难的,因为读者可能既没有受过数学训练,也没有足够的数学知识,这意味着作者必须抛弃平时的阅读和写作手法。于是自然地,首要的问题是:这可能吗?欣慰的是,Serge Lang(编者注:美国数学家、教育家、社会活动家)的杰出工作充分地证明了其存在性,数学系的学生必定听说过他——他的多本砖头般厚度的数学教科书让研读它们的学生欲仙欲死。但这位以写书风格枯燥繁杂著称的数学家,却出版过一本平易近人的《做数学的美妙》(The Beauty of Doing Mathematics),里面包含了三次他面向大众的演讲。他的处理方法是:在讲每一个具体的有数学价值的问题时,他都会与听众互动讨论,以此来揭示纯数学为何。这本书是如此成功地将公共名声“臭名昭著”的数学解释得让家庭主妇都有兴趣且多次光顾,以至于笔者一度以为这是唯一可能的数学科普方式。
另一个关键的问题是:读者想学到什么。数学科普书的读者群一般是中学生和其他对数学感兴趣的非理科人士。笔者相信大部分读者的兴趣点在于了解深刻的数学:他们没有精力或者能力来阅读数学教科书,于是只能退而求其次地通过数学科普来了解数学。这也是Serge Lang所著书的致命伤:他仅仅打开了几扇窗,展示了数学是具体怎么做的,以及为什么数学是有趣的,却没有展示真正有趣的数学,进而真正改变人们对于世界的认识。
不可否认,Serge Lang的书是最为优秀的数学科普之一,但这一缺失实属遗憾。然而,这一要求对数学科普来讲是否太高了?不用数学工具真的可以理解数学结果吗?不消多说,绝大部分数学结果都不能用自然语言描述,尤其是现代数学。即便顶尖数学家都极有可能无法读懂非自己所专攻的领域的论文,甚至可能连定理陈述都不能理解。 然而,高尔斯的杰出工作表明,对于一些关键性的数学思想,可以借助自然语言解释清楚其大略。希尔伯特曾说,真正的数学家能向农夫解释清楚微分几何是什么(尽管这是数学界中为数不少的流传甚久却又未经证实的轶事之一)。
于是,一个问题自然地被引申出来:在撰写数学科普时,如何选取既在数学上是重要的,又可以被自然语言和初等数学解释清楚的材料?这也是很多科普书的失败之处。 高尔斯就在《数学:极简导论》的前言中就吐槽了目前充斥于科普读物中的哥德尔完全性定理和混沌理论:它们是重要的,但其所占据的篇幅远远超过了它们在数学中的应有的部分。具体而言:哥德尔定理不是所有数学家都感兴趣的,M. Kline在《数学:确定性的丧失》(Mathematics: The Loss of Certainty)中提及上世纪初(国内数学史中常称此阶段为第三次数学危机)大多数数学家并不关心数学基础,而且理解哥德尔定理需要以一定的数理逻辑为基础;混沌理论的基本思想只是确定性系统中初始值的微小偏差对结果造成的巨大影响,而具体的数学理论和结果都很难用自然语言讲明白。
而且,更为重要的,普通读者对其的理解极易造成偏差,例如忽略哥德尔定理的适用条件(以为所有理论都不自洽)和不理解混沌效应何时失效(日食为何可精确预测),反而可能会让读者产生错误的认识。
就笔者狭隘的阅读面来看,成功解决了以上这几点的只有蒂莫西·高尔斯的《数学:极简导论》。
高尔斯的写作方法是专注于深度:尽可能地将要讨论的问题用自然语言和初等数学工具讲明白。他选择的几个专题都是当之无愧的、人类心智的荣耀,标志着人类对世界认识的重大跃进。下面以书中第三章“证明”为例,具体来看高尔斯是如何出色地完成了三个要求。
首先,高尔斯对选定的材料讲解的十分清晰。一个根本性的数学原理是数学证明的有效性在原则上是可验证的,高尔斯以“根号2是无理数”为例将这一重要结果的想法说得非常清楚。他将传统的初等证明一再分解,直到直观上无可置疑的程度,然后在延伸阅读部分向对他的分解还不满意的读者推荐了罗素的《数学原理》(Principia Mathematica)中“1+1=2”的证明,希望借此表明任何严格的数学证明都可以在有限步后化归到公理当中。
其次,高尔斯的选材尤其值得称赞。在这一章的结尾,高尔斯选择了三个看似显然但严格证明却是困难的例子。高尔斯难能可贵的地方在于同时做到了以下四点:
(1)挑选出了不需要什么数学知识就可以理解的命题
(2)这些命题颠覆了人们习以为常的直觉
(3)将这些问题的困难之处说得非常明白
(4)这些命题本身都是具有数学价值的。
其他几点书中展现地非常明显,但第四点高尔斯可能出于对读者水平的考量而并未展开,笔者在此稍作补充。第一个例子是算术基本定理的唯一性,类似的例子在抽象代数中一再出现;第二个例子是三叶结,Allen Hatcher在《代数拓扑》(Algebraic Topology)将其作为基本群的基本动机;第三个例子是Jordan曲线定理,几乎所有人刚听到的时候都以为是trivial(显然、无需证明的),是最为经典的反直觉命题。
上世纪最为重要的数学家之一Michael Atiyah在演讲《数学的变迁和进展》中指出:“理解数学发展的最佳途径是,把它看做是对于问题的日趋困难与复杂所作出的自然回答。只要这些问题是直接或间接地植根于自然科学和其他的科学分支之中,其复杂性本身就反映出了现代科学的相互覆盖和歧延的特性。”[4]由于篇幅和读者水平的限制,高尔斯在文中并未涉及数学史以及其他有助于理解所讨论问题的重要性和深刻性的材料。笔者尽可能地补充了本书三、四、五章中高尔斯一笔带过或者省略的材料,以方便读者更好地体会作者的良苦用心和增进对此书的理解。
芝诺悖论(包含一系列悖论,其中最有名的是“飞矢不动”“阿基里斯无法追上乌龟”等)以最简洁的纯逻辑论证了人类其实并没有真正明白那些直觉中看似显然、毫无困难的概念,比如运动的概念[5]。从这一悖论的提出到数学家彻底严格地定义极限,跨度超过了两千年,站在无数数学家的肩膀之上,人类才可以说自己真的明白了运动的概念。当然,这并不意味着人类明晰了运动的“本质”是什么,例如“运动是不是连续的”这类物理问题以及牵扯到的哲学议题。
极限是高等数学和初等数学之间的一道门槛,但是其ε-δ语言刻画的极限定义(入门课程清一色地采用这一古典定义)往往令初学者望而生畏,即使是受过严格训练的数学系的学生都不容易迈过这一道必须迈过的坎,更何况对于大众来说。但人类理智的这一巨大成就就注定只能被少数人理解吗?高尔斯尝试做出改变。
在《数学:极简导论》的第三张章极限与无穷中,高尔斯讲解了三个具体的例子——无理数的十进制展开、速度的定义和面积的定义来让读者对极限有一个直观的体会。在每一个例子中,他其实都将极限的定义伪装在了自然语言之下。我相信,每一个认真阅读了这三个例子的读者都能把握极限的基本思想。笔者在此对高尔斯的叙述做一些补充。
首先是无理数的十进制展开。实数的定义方法有很多,高尔斯采用的是十进制小数的定义方法[6]。其中关于的解释笔者持怀疑态度。高尔斯认为只是一个惯例规定而已,否则会导致一些怪异(但逻辑自洽)的结果,但笔者认为良定义的方法是作为无穷级数的和,那必然等于2。实数系作为有理数的完备化,很多有理数系下的性质应当还是成立的(至少对于高尔斯提到的推出)。
其次是速度的定义。即使独立创造微积分的牛顿,他对连续这一基本概念也思考不清楚。但值得注意的是,即使极限停留在不严格的定义阶段,微积分也有着迅猛的发展。这意味着,数学家们在对极限的运用过程中已经养成了关于极限的直觉。
这实际上是数学中严格性和洞察力的矛盾。人们往往夸大了严格性的重要性,一个例子是数学在实分析初创阶段,因为数学界内部某些权威认为这一理论不够严格,而险些被扼杀在摇篮中。另一个例子是身为最具原创性数学家之一的Michael Atiyah(编者注:英国数学家)也强调数学的发展依赖于开拓者的直觉这一属性,他在演讲《如何进行研究》中提到:“严格的数学论证的作用正是在于使得本来是主观的、极度依赖个人直觉的事物,变得具有某种客观性并能够加以传递;我完全不想拒绝这类直觉带来的好处,只是强调为了能向其他人传播,所获得的发现最终应以如下方式表述:清晰明确、毫不含糊,能被并不具备开创者那种洞察力的人所理解。”[7]我想,实践者达成的共识比旁观者介入的争论更有价值。
最后是面积的定义。面积的计算是微积分发展的一个主要动机,龚昇所著的《简明微积分》就以定积分出发建构了整个初等微积分理论。这一节的主要缺陷是介绍了阿基米德对圆的面积的解释。通过多边形来逼近圆的做法有利于直观上理解为什么圆的面积是这个样子,但是不加说明地应用这种方式容易让初学者误以为无穷多个无穷小之和为零。读者可能无法回答为何下图的做法是错误的。
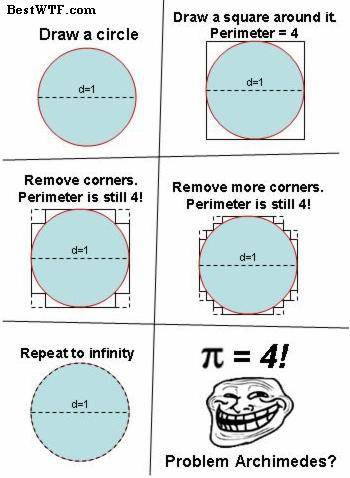
这一看似显然的问题可以很好地检验学生是否理解了极限概念,一个反面例子是我国高中数学第一次引入极限内容的时候,许多高中教师无法回答用无限分割来“证明”直角三角形的斜边等于直角边之和的错误。此外,高尔斯直接规定了矩形的面积计算公式,其实一旦假定面积的平移不变性(平移后的图形面积不变,这一假定是自然的),可以证明矩形的面积与长和宽的乘积呈正比[8],再人为规定其比例为一即得面积公式。
这一章一个极大的遗憾是没有提实分析中的测度理论。芝诺悖论是最为重要的悖论,因为悖论本身逻辑清晰,而且自问题提出后数千年都没有完善的回答(值得一提的是,单单借助极限本身只是重述了问题而非回答)。唯一清楚没有歧义的解释是不可数个可测集没有可加性,这一回答背后隐藏着人类直觉的一个缺陷,即无限也有相对多少(例如整数可数,实数不可数),一个常见的错误就是简单地认为对可数成立的性质在不可数的情况也一样成立。类似的例子还有选择公理(简单来说,有无限多个装有球的盒子,你可以从每个盒子中拿出一个球),如果承认这一看似显然的公理,可以推导出分球悖论(Banach-Tarski paradox),即将一个三维实心球分割为有限多份,然后仅仅通过旋转和平移重新组合,可以拼成两个半径和原来相同的完整的球。旋转和平移显然是体积不变的运动,这违反了人们根深蒂固的体积守恒观念。
当然,对选择公理的科普极有可能导致前文所提到的读者一知半解的情况。但笔者认识,芝诺悖论本身是极富价值的,完全可以也应该花费一定篇幅将其讲解清楚[9]。此部分建议将一个例子拿出来,然后进行全是,而不是一个例子仅做简单介绍,这样只明确了概念,而不动究竟哪些是有悖常理的。
关于维度最通俗的理解应该是笛卡尔的坐标法,即确定一个点的位置需要的坐标数量,这一处理方法是代数的。当然这并非唯一的途径,然而这一理解不仅在低维是自然的,也可以毫无困难地推广到高维。高尔斯在这一章主要解释了为何考虑四维空间乃至高维空间是有意义的。这实际上是数学哲学的根本问题之一,即数学对象何为。
高尔斯的数学哲学观念受到了维特根斯坦(编者注:Ludwig Josef Johann Wittgenstein,犹太裔奥地利裔英国作家、哲学家)后期哲学思想的影响,作者也在后记中有所提及。由于《哲学研究》为语录体,主干思想并不清晰,故借用维特根斯坦的权威传记《天才之为责任》(Ludwig Wittgenstein: The Duty of Genius)中的说法来简要描述维特根斯坦的基本想法:“‘数学关心的是发现真理’这整个观念是一种随着纯数学的兴起和数学与物理科学的分离而产生的错误。”、“维特根斯坦的手法并不是重新解释某一具体事物的证明,而是如此这般地重新描述整个数学,使数理逻辑呈现为他相信是它之所是的哲学错乱,彻底消解掉数学之为一门发现关于数学对象(数、集合等等)的事实的科学的图画”。
按维特根斯坦的看法,没有任何东西是等着数学家去发现的[10]。但笔者对高尔斯会研究维特根斯坦的数学哲学的细节持怀疑态度,因为高尔斯还引用了罗素《数学原理》的结果,而维特根斯坦从原则上反对以逻辑作为数学的基础。值得注意的是,高尔斯采纳的这一哲学观点与大多数数学家不同,数学界更为常见的态度是“数学家们在工作日都是实在论者,但在周末则都变成了形式主义者。”[11]尽管类似于近代科学哲学与科学已经没有什么联系,数学哲学也往往沦为哲学家的自娱自乐(而不像上世纪初有不少顶尖数学家参与),但不可否认这一思想观念对高尔斯的影响。维数这整一章,乃至于整本书都是基于这一哲学观念的基础之上。
一旦认识到了这一点,这一章高尔斯编排材料的顺序就显得极为自然,尤其可以更好地体会精彩的“四维空间能否可视化”(Can Four-dimensional Space be Visualized)一节。传说一些数学家可以看到高维空间,例如J. Milnor的经典构造七维怪球(exotic 7-sphere)就是Milnor直接想象出的。高尔斯写到“投身于数学研究的一大乐趣是,随着个人的专业娴熟程度的增长,可以‘直接看出’很多原本需要数小时才能解决的数学问题的答案,而且这一能力不局限于几何领域”,所谓的“看出”(just see),换个说法,就是直觉。
直觉,并非是先天就有的,而是后天训练而得的。这一特性也并不仅限于数学领域[12],但因为数学涉及的部分直觉深深扎根于日常体验,因而效果更为明显和强烈。比如,不少人在刚接触三维几何,也就是高中的立体几何时存在极大的想象困难,但伴随不断的练习,想象力会有明显提升。同样地,尽管日常生活中没有高维几何的体验,但随着不断接触,就能培养出高维几何的直觉。这是那些传奇数学家的超人能力的一个可能解释,高尔斯提到,“一些专攻四维几何的数学家对四维的可视化能力有着显著的提升。”这是数学提升人对世界的认识的重要例子。
为了说明这一认识的重要性,可以设想一下生活在二维世界的生物或许会对我们习以为常的三维世界无比惊讶,例如他们不能想象进食和排泄可以使用不同的口[13]。但人类不也只是生活在三维世界而已,有太多的东西是我们单靠日常的直觉无法想象、甚至不可理喻的(比如弦论中的Calabi-Yau流形)。数学赋予了我们探索未知世界的坚实武器,而不是仅仅停留在科幻层面的恢弘想象力。
高尔斯可能出于读者或者篇幅的考量,并未涵盖这些背景知识,但笔者认为这一背景资料对理解维度的意义是有价值的。
弯曲空间一度被认为是不可能的,康德在《纯粹理性批判》(Kritik der reinen Vernunft)中特意论证了为何欧式几何是唯一可能的几何。即使非欧几何(即常曲率空间的几何,最早的例子是罗巴切夫斯基几何)早在十九世纪就被提出,大部分数学家认为这只是采取了特殊的度量下所定义的直线(一些经典的非欧几何模型都是如此),还是嵌入(embed)到了欧式空间。尽管高斯绝妙定理(Theorema Egregium)就有了非欧式空间的部分性质不依赖于这一空间如何嵌入到欧式空间的思想的雏芽,但直到爱因斯坦的广义相对论的发表,人们才真正严肃地对待这一曾被当做扶手椅上的(一种经典比喻,常被认为是对哲学家/数学家的讥讽)毫无实际意义的思想。可惜的是,时至今日,这一伟大的想法并没有普及给大众。
John Stillwell在《几何学的四大支柱》(Four Pillars of Geometry)中展示了几种互相等价的但洞察点不同的角度来理解几何,其中最为自然的显然是欧式几何的角度(笛卡尔的解析几何和欧式几何其实是一回事)。和高维几何相同的道理,最为自然的看法并不一定是正确的。爱因斯坦不朽的杰作广义相对论就揭示了时空的本性不是欧式的。值得注意的是,这一结论并不需要爱因斯坦一定是正确的前提之下才成立,因为为验证他的理论是否正确的实验有力地说明了时空不是欧式的。
要理解弯曲空间是什么,必须明白两个问题:
(1)空间的弯曲是什么
(2)为何在不嵌入欧式空间的条件下研究弯曲空间的形态是可能的。
回答这两个问题并不轻巧:第一个问题实际上是度量,而度量这一概念的定义是建立在很多前置知识的基础之上,犹如高尔斯在前言中提到过的Hilbert空间的例子;第二个则更为困难,因为我们的日常经验完全是欧式的。
高尔斯详细地解释了为何在球面几何中用大圆来定义直线是合理的,随后进一步地用双曲几何(Poincare圆盘模型)说明了度量是什么(二者的顺序安排是非常精彩的,高尔斯在书中自己做了解释)。他着重于解释为什么仅仅使用这个非欧式的空间本身就够了,根本不需要借助于欧式空间。换句话说,并不是因为将这些空间嵌入到欧式空间会带来计算上的复杂才采用了一种新的度量,而是根本没有必要嵌入到更高维的欧式空间。而第二个问题,他采用了最为直观的三角形内角和来表现,其数学原理就是Gauss-Bonnet公式。
事实上,惠特尼嵌入定理(Whitney embedding theorem)保证了以上讨论的非欧空间都可以被嵌入到更高维的欧式空间中。但正如奥卡姆剃刀所陈述的,“若无必要,勿增实体”。问题的本质无需增添人为的结构就能解决。陈省身先生的成名作就是通过活动表架法优雅地解决了Gauss-Bonnet-Chen公式,而这一结果事实上之前已经有了一个通过引入人为的欧式结构来证明。Marcel Berger在其试图涵括黎曼几何的恢弘成就的大作《黎曼几何概览》(A Panoramic View of Riemannian Geometry)中专门设置章节探讨了陈先生的工作是如何对这一学科的发展起了极为正面的影响。这也是Thomas S. Kuhn在《科学革命的结构》(The Structure of Scientific Revolutions)的核心论点的一个具体事例。
对于初学者,这可能是最易理解的。唯一的遗憾是高尔斯没有明确说明三角形三条边一定是测地线(给定度量下的直线)。笔者在中学阶段阅读科普读物时在这一问题上就困惑不解,我当时的想法是:内角定义为两边的有用切线的夹角,但如果给定了三角形的三个点不能保证边的唯一性的话,那么内角就不是被完善地定义(well-defined)的。尽管这可能是出于笔者的愚笨,但简要提到一些技术问题可能更好。此外,这一章有一个无关紧要的科学史的问题,Arthur Eddington对广义相对论的实验验证可能存在问题[14]。
广义相对论的科普书籍解释时空弯曲时往往(不得已)采用并不准确的图示,但可惜的是这些书没有花笔墨去阐释清楚弯曲空间到底是什么,或者效果欠佳。比如说大众中最为知名的科普书之一——S. Hawking的《时间简史》(A Brief History of Time)——在这一点上也不幸失败。而高尔斯则完全关注弯曲空间本身,甚至于进一步花了不小的篇幅试图介绍流形这一现代数学中最为基本的概念,而不是忙于介绍高深莫测的概念和填充科学角落的八卦这些读者们可能更感兴趣的内容。 这是人类认识世界的一大跨步。本节的开头提到了人类原先对弯曲空间的认识,罗素在《哲学问题》(The Problems of Philosophy)中以此反驳康德的哲学体系,这充分体现了数学是如何强大地打败了根深蒂固的直觉,而在没有数学的帮助下这种直觉曾误导了人类最为卓越的头脑。
第二章“数与抽象”中,高尔斯试图表明,如何将日常熟悉的自然数及其运算规则抽象化。这是数学发展的重要方法:提取原理论中最为重要和核心的内容,将其推广以发展出更为一般的抽象理论。但高尔斯在过程中引入了太多的规则(或称公理),远超所必须的数量,这违反了抽象过程中的简洁法则(当然,这样的安排可能是出于易读性的需要)。数学上更为漂亮的处理办法是从Peano公理出发[15],极好的参考书目是陶哲轩《分析学》(Analysis I & Analysis II)的前六章,高中水平的读者即可无太大困难地阅读:笔者至今还清晰地记得发现加法交换律居然可以从那么显然的几条公理中推导出来的兴奋之情。尽管如此,人工的痕迹比高尔斯现在采用的方法更为明显,但高尔斯由于引入了太多的规则,对于读者来说这一章的脉络极有可能是模糊的。
此外,高尔斯以方程的根作为数系扩张的动机是欠佳的。高尔斯的逻辑是,限制在正实数域上的一元一次方程有时会无解,那就引入负数;同样地,为了让一元二次方程永远有解,无理数和复数就应该被引入。也就是说,既然可以抽象地扩张数域,那自然地就应该在哪怕没有其他动机的情况下也要扩张数域?
首先来看无理数。笔者在初中第一次接触到无理数时也是类似的想法,甚至觉得古希腊人愚不可及:明明无理数会自然地出现在很多数学中,还一定要坚守有理数才是唯一可能的呢。但了解数学史后,才意识到有理数的思想有着深刻的哲学背景,即原子论:既然任何事物都是由基本的原子所组成的,那么任何有限长度都仅包含了有限数目的原子,于是相对于给定的单位长度的比值一定是有理数,这也是有理数的正确含义“可比数”的本源。
这一问题在初中阶段困惑了我相当长的时间,直到明白了无穷小的含义后才发现错误的所在:如果原子的长度有下界,那么能表现的量一定是离散的;如果原子的长度是无穷小,那么任何有限长度都包括了无穷数目的原子。这是对直觉的重大反思,也是人类认识世界的一大跨步,高尔斯匆匆跳过甚是可惜。
同样的,对于负数和复数的解释也欠佳。M. Kline在《数学:确定性的丧失》中的基本论点是:数学的发展来源于对自然的合理诠释,这一论断至少对于现代数学之前的发展是成立的。人类对负数的认识是相当晚的,笛卡尔的直角坐标系中都没有出现负轴。这背后的真正原因是正数在当时已经够用了,没有必要再不直观地扩张。教材中复数基本都是从X2+1=0 引入的,但必须注意的是,这只是最为方便的讲法罢了。真实的原因是:复数是对平面运动的自然描述[16]。当然,高尔斯的这种提法可能是提炼自从纯数学本身出发和演化的Galois理论的基本思想。
第七章 “估计与近似”稍稍弱了一些。对近似的讲解与第四章“极限与无穷”有所重叠,对数和平方根的近似略显浅陋和粗糙,其本身的重要性也不大,主要是为下一节的素数定理作铺垫。尽管素数定理毫无疑问是重要的数学结果,但它对人们认识世界并没有特别重要的意义。高尔斯在讲解中提到了概率模型,笔者非常遗憾他没有就概率模型的应用深入下去。尽管他在第一章就提到了这类模型的缺陷,但这并不是忽略的好理由。
数学在其他学科中应用极大的应该是统计学,统计学的蓬勃发展也预示着数学对于日常生活的重要性的提升。统计学的思维方式可以极好地帮我们判断信息的价值,这点在这个信息膨胀的社会是实用的能力。这一章,如果能关注于统计学最基本的想法,对于读者或许更有价值。
第八章“常见问题”则非常有趣,一个顶尖数学家对一些坊间常见的误解给出了自己真诚的答案,其中“数学家三十岁以后就是过去式了?”“为什么有许多人明确地讨厌数学?”“业余爱好者解决过著名的数学问题吗?”等问题尤其精彩。即使是数学系的学生,相信也能从中获益良多。
总体而言,高尔斯的这本书最大的欠缺可能是对于数学史的不够重视。我能充分理解高尔斯的做法。对于以数学为置业的人而言,过多的历史/哲理探求是毫无意义的。正如丘成桐先生所批评的,“现在经常有来自中国大陆的学生大谈数学的哲学,而不能坐下来做扎实的计算。”但鉴于本书的读者对象是数学行外人,我觉得很重要的一点是祛魅,破除数学的神圣性。
一种常见的对数学的误解是将数学视为一堆天才凭空搭建出的空中楼阁,很多人对数学的惧怕也由此而生。优雅的数学结构从来不是数学工作者在彻底无知的黑暗中探索而打磨出的,而是基于对前人工作不停地深入反思和提炼,即所谓的“站在巨人的肩膀”。Benedetto Croce在《历史学的理论与实际》(History: Its Theory and Practice)中断言“一切历史都是当代史”。在数学史上发生的种种都一而再地在当代重演。对非线性地发展的数学史的彻底无视可能并非好事。
数学极大地改变了人类对于世界的认识。数学的一个常被忽视的价值是对人类直觉的弥补,而这一任务往往被视为是物理的,但事实上,数学中有着极多的对日常经验和直觉的不足或者错误的修正。遗憾的是,大多数人不知道这些思想,而更为可惜的是,渴望了解的人甚至不知道该读什么书籍。笔者以为,数学家有这个义务让读者知道该读什么,这也是在数学科普书中最应该探讨的内容。科普书不应该满足于向读者介绍些远超他们认识能力的前沿概念,或者提供些科学边边角角的八卦,倘若如此,科普书对读者的作用极有可能沦落到增长谈资和培养偏见。
一种常见的甚至是根深蒂固的误解是读者不可能不借助数学技术工具的帮助而真正理解这些材料。但问题的关键是,何为“理解”?比如,我们可以理解极限吗?维特根斯坦提出ε-δ语言只是一套自洽的叙事体系而已,并没有让我们真正明白极限的本质是什么。数学家们通过一定的练习,能够熟练使用这套语言,明白其各种性质,但这并不意味着他们真的理解了极限本身。
继续追问下去的话,对于基础代数,乃至基本的加减法,我们又何尝不是通过练习可以熟练地应用。数学家身上或多或少有着傲慢:数学是唯一能让我们感觉到拥有绝对确定性的知识。但似乎并没有什么有力的证据来支持这并非是我们一厢情愿的幻觉。John von Neumann曾坦言:“年轻人啊,在数学中你从来不是理解东西,而是适应它们。”[17]
抛开哲学上的技术困难,有一点是清楚的:数学的训练增长了我们从数学直觉里获得的益处,至少受所谓严格性不足的危害会减少,而且越是随着数学的学习,这种能力就越会得到提升。同样地,没有什么数学能力的大众也具有可以培养数学直觉的可能,即使相对于数学家而言是渺小的。他们完全可以从数学中学会认知世界的新的方式,以使自己的直觉更为正确。
笔者很欣喜有顶尖数学家愿意撰写数学科普书籍——用心写作科普对于他们来说并不轻松,甚至可能比学术研究更为困难。维特根斯坦的《逻辑哲学论》中有一句常被忽视的点睛一笔:“我表述的命题在这种意义上起阐明作用:人们借助它们,穿过并越出它们,理解我的人最终将发现它们是无意义的。他必须越过这些命题,才能正确地看世界。”(6:54)[18]谨以这句话,向高尔斯致敬。
引文及注释:
1,中译本为《普林斯顿数学指南》,蒂莫西•高尔斯主编,齐民友译,高等教育出版社,2014年。
2,中译本为《数学》,蒂莫西•高尔斯著,刘熙译,译林出版社,2014年。下文对原书的引用为笔者翻译,参考了中译本。
3,这一系列国内有两种译法,分别是译林出版社的“牛津通识读本”,以及外研社的“斑斓阅读”。
4,以下引文摘自《数学的同一性》,阿蒂亚著,袁向东译,大连理工大学出版社,2009年,第15页。
5,关于芝诺悖论的具体论述和微积分概念发展的极简史可参见《重温微积分》,齐民友著,高等教育出版社,2004年,第一章。
6,这一思路完整的定义方法可参考《实变函数论》,王昆扬著,高等教育出版社,2001年,第一章。
7,以下引文摘自《数学的同一性》,阿蒂亚著,袁向东译,大连理工大学出版社,2009年,35页。
8,证明概要如下:沿长方向平移长度,所得的矩形的面积与原矩形相等,考虑到原矩形和平移后的矩形组成的矩形的面积为原矩形的两倍,故面积与长度成正比;同理可证明面积与宽度成正比。
9,一个卓越的例子是UCLA的数学博士木遥撰写的科普《长度是怎样炼成的》,参见http://imaginary.farmostwood.net/21.html.
10,均摘自《天才为之责任》,瑞·蒙克著,王宇光译,浙江大学出版社,2011年,分别为第333页和第422页。另,维特根斯坦在《哲学研究》中的数学哲学并不足以代表他的观点,更详细的可以参见《数学基础研究》,维特根斯坦著,韩林合译,商务印书馆2013版。
11,《二十世纪数学哲学》,叶峰著,北京大学出版社2010版,第29页。
12,康德提出一种哲学上的依据,认为这受到了先天的认知框架的限制。现代的心理学观点可以参见Gary Kline, Sources of Power, the MIT Press, 1999以及Daniel Kahneman, Thinking, Fast and Slow, Farrar, Straus and Giroux, 2011, ch 22.
13,这方面更为详实的材料很多,Edwin Abbott的Flatland应该是这一方面最富盛名的著作,Ladd Ehlinger Jr.导演的动画电影Flatland是原著较为忠实的表现。
14,具体可参见《太阳的故事》,卢昌海著,清华大学大学出版社,2011年。书中第五节“插曲:爱丁顿在1919”对这一问题有着详细的论述。
15,另一种处理方法是集合论的,但方法技术细节过多,且远没有Peano公理直观,不适合普通读者。
16,可参见《复分析:可视化方法》,尼达姆著,齐民友译,人民邮电出版社,2009年,第一节。 此外,本书齐民友的译后记中对这个问题也做了分析。
17,引文摘自Zukav, Gary. The dancing Wu Li masters: An overview of the new physics. Random House, 2012.
18,中译文引自《维特要斯坦的:文本疏义》,黄敏著,华东师范大学出版社,2010年,第473页。















