本文内容整理知乎专栏：天上不会掉馅饼，有删节。
只要不去贪图不正常的高息，任何旁氏骗局都将对你无可奈何。
一、天上不会掉馅饼
最近总
有大量的人找到我，问了我不少关于某某某公司，某某某理财产品是不是骗局这类的问题。很遗憾的是，几乎所有来问我的朋友都遭遇到了不同程度的骗局，有的骗局涉案金额高达十几亿美元。
有意思的是，骗局几乎清一色都是各种变种的
旁氏骗局
。
所谓旁氏骗局指的是，做局人给受骗者以高利息的承诺，但是事实上并没有任何增值的项目，纯粹是拿后来者的投资款来支付之前受骗者的利息。
例如，一个做局者声称1个月能给投资者带来10%的回报。第一个受骗者投资了100万，而做局者并没有投资任何一个项目。等到下个月的时候，他拿第二个月新来的投资者支付的钱中抽取10万给第一个投资者。
当然，我们知道没有真正的赠值项目作为支撑，这样的骗局终会有结束的一天。
然而，那如何鉴别一个投资项目是不是旁氏骗局呢？
其实，
最明显的特征就是不正常的高利息。
也许你觉得一个月10%的利息不算高，我来讲个小故事。
传说西塔发明了国际象棋而使国王十分高兴，他决定要重赏西塔，西塔说：“我不要你的重赏 ，陛下，只要你在我的棋盘上赏一些麦子就行了。在棋盘的第1个格子里放1粒，以后每一个格子里放的麦粒数都是前一个格子里放的麦粒数的2倍，直到放满第64个格子就行了”。
区区小数，几粒麦子，这有何难，“来人”，国王令人如数付给西塔。
计数麦粒的工作开始了，还没有到第二十格，一袋麦子已经空了。一袋又一袋的麦子被扛到国王面前来。但是，麦粒数一格接一格飞快增长着，国王很快就看出，即便拿出全国的粮食，也兑现不了他对西塔的诺言。
原来，所需麦粒总数为18446744073709551615。这些麦子究竟有多少？大约820亿吨。按照现在全球大麦产量来看，大概550年才能满足。
这就是复利所带来的奇迹。
可能大家觉得10%的月回报不算高，看下图
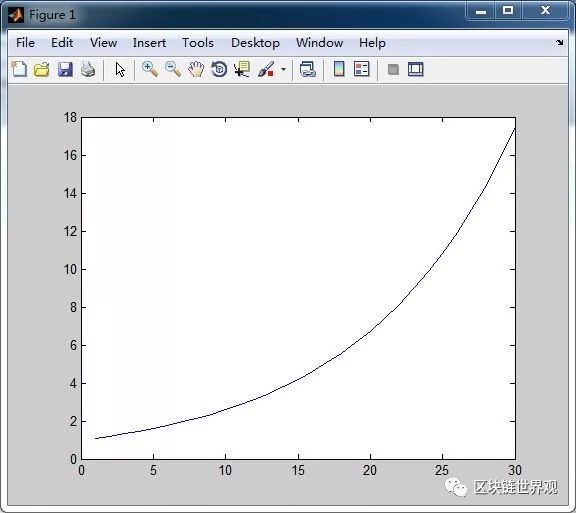这就是如果有10%的回报率，那么到第二年，也就是第24次复利将会是9.8，接近10倍。满3年的时候，就是31倍。20年则会达到86亿倍的汇报的惊人回报。
你现在投资1万元，20年后就是86亿倍的回报，也就是86万亿的财富，数量相当于去年美国的GDP总量。你才投入1万元哦！
说到这里，大家应该明白了，
10%的月回报的投资机会是不会主动找上你的。
世界上确实存在月回报10%的投资机会，但容量会有上限
，这种稀缺的机会，是不会主动来找你的。因为市场有冲击成本。也就是说，如果用同一个策略的人多了，则该策略需要购买的资产同时就会有价格波动，从而无法再以策略需要的价格购买到。
所以，再次告诫大家：
天上不会掉馅饼
。
二、何时高潮？何时破灭？
旁氏骗局的特征是如此的明显，但屡试不爽。旁氏骗局会完蛋确实毋庸置疑，让我们感兴趣的是旁氏骗局
什么时候会发展到高
潮，什么时候破灭？
索罗斯在他的著作中，提出了
『反身性』
的模型，以颠覆传统的经济学解释。
索罗斯给出的模型提出了两个离经叛道的观点。
2.1 何时高潮？
股票的价格并非围绕股票的价值而波动，而是具有“反身性”。即过去价格的提升带来升值预期，故而新进入的投资者会买入持有。
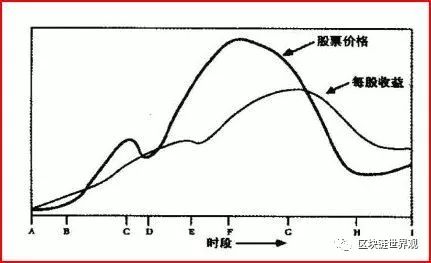
买入持有者并不是看好每股收益而购入，而是他们预期股价会继续上涨，可以卖给后来的投资者。
虽然股票的价值有升值空间，但
投机者在这里预期的事情和庞氏骗局是差不多的
。即，
我所期望的收益是后来的加入者给出的
。
所有的人都盼望着后来的加入者加入进来，
但参与者的上限，或者说参与者的资金上限并不是无穷的
。
这导致整个过程必然面临和旁氏骗局一样的后果——泡沫的破灭。
不同的是股票毕竟是有价值的，而一般的庞氏骗局背后没有任何有实际价值的东西。也就是说，当股价一路下降的时候，一样会产生正反馈效应，后来的做空者会预期价格更加低，所以更加卖出。而前期的投机者会产生类似踩踏事故中的情况。
一旦股价下跌到，光持有股票，获得的股息也是一笔不错的投资时。套利者就会出现，或者我们可以叫他们“价值投资者”。光持有这些廉价的股票，赚取股息即可获得不错的回报率。
这是第一个离经叛道的观点，不围绕价值简单波动，投资者自己的行为本身是影响未来价格的因素。
2.2 何时破灭？
第二个离经叛道的观点是，当价格被投机者推高的时候，该上市公司的融资能力会增强而导致本来的价值提升。买股票的人多了，这公司的融资能力会帮助其扩展业务。
下降的时候，会有类似银行挤兑的现象。本来基本面良好的公司可能因为惨烈的股价下跌而遭受损失，造成该公司的价值受损。
观察者本身会影响被观察到事物，而非经典模型的观察者无关。
我们这里定义一下
『
广义的旁氏骗局
』
：
投机者都希望后来投机者的新入资金推高而产生收益，而非看好该资产本身能产生的价值。
三、庞氏骗局的数学模型
回顾旁氏骗局的过程，都是惊人得相似。一开始投资者会非常谨慎得小小尝试一下。
等到实验3次都成功后 ，就会变得疯狂起来。
借助杠杆是不可阻挡的事情。但所有人借助杠杆都是有上限的。
故而我们用正态分布做假设搞了个模拟的样子。
syms x;f1=exp(-((x-10)/5)^2);s1=int(f1,x);s1=simple(s1)
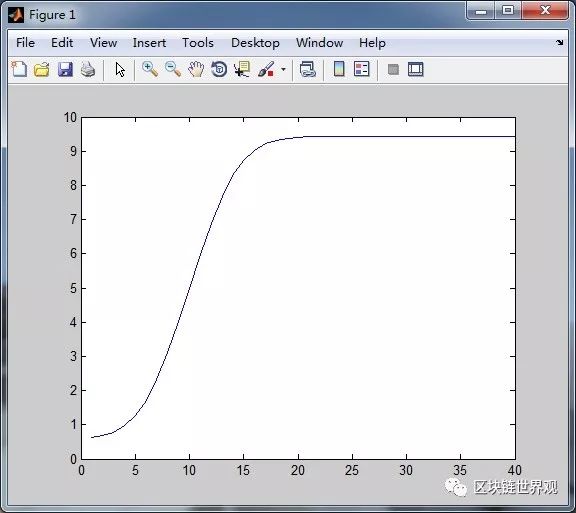这根曲线的意思是，一开始的入金是比较缓慢增长的，
实践成功5次左右，就会飞速增长入金，然后达到杠杆的最大限度，开始收敛。
而出金的意愿也是和融资能力相关的，
出金的意愿在一开始尝试的时候是比较强的。
尝试旁氏骗局第一次成功后，会要求出金，试试是不是真的赚到钱。
而尝试成功多次后，就会要求利滚利，不会要求快速出金，直到融资的能力遇到上限。被迫提高出金意愿。
因为必须兑付一部分利润给融资的来源方。
P=(x-10)^2/500;er
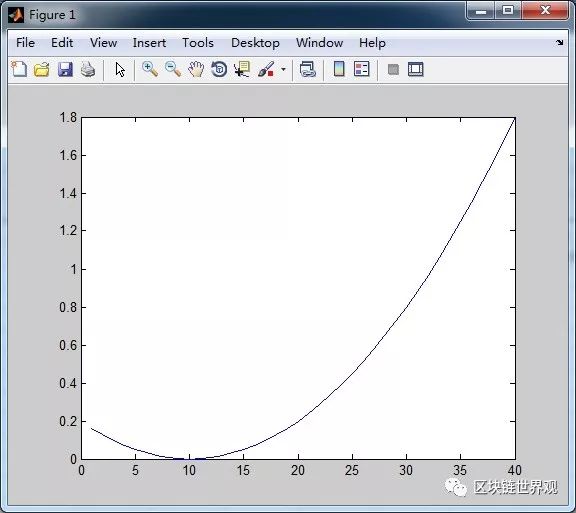上面这图就是出金意愿的曲线图，
到实践到第10次左右，是不愿意出金的。
最后，我们用N(n)来模拟每个月做局者的现金流入，是一个递归函数，每次都是以上一次的入金和受骗者自身的情况而定的。
O(1)=0;I(1)=(5*pi^(1/2)*erf(1/5 - 2))/2+5;N(1)=I(1);P(1)=(1-10)^2/500;for i=2:40
MO=((5*pi^(1/2)*erf((i-1)/5 - 2))/2+5-O(1))*(0.1+(i-1-10)^2/500);
O(i)=MO;
I(i)=(5*pi^(1/2)*erf(i/5 - 2))/2+5;
P(i)=(i-10)^2/500;
N(i)=I(i)
