专栏名称: 协和八

协和八，小医生的大世界！源自协和的品牌，让临床妙趣横生，让思考更真诚，让生活更奇妙。

天啦噜！没考虑到混杂因素，后果会这么严重？| 协和八

协和八 · 公众号 · 医学 · 2017-06-01 20:35

正文

说人话的统计学

在前两集文章里，我们为大家介绍了当自变量不止一个时，如何建立多重线性回归（即包含多个自变量的线性回归）模型（《自变量不止一个，线性回归该怎么做？》），以及随之而来的新问题——交互效应的意义（《找出「交互效应」，让线性模型更万能》）。

多重线性回归的一大作用，是帮助我们同时分析多个因素与因变量之间的相关关系，并且考察这些因素（自变量）之间的交互效应。

今天，我们将一起讨论多重线性回归的另一个重要价值——在统计推断中排除混杂（confound）因素的影响。

什么是混杂因素？为什么多重线性回归能帮上忙？我们将通过一个例子来展开今天的讨论。

让我们回到孩子身高的问题中，想象一个新的情景：

我们重新收集了若干对蓝精灵兄弟或姐妹（每对兄弟或姐妹的年龄差距相同）的身高，想研究同一个家庭中，年龄较小的蓝精灵孩子（以下简称为「小孩子」）的身高与年龄较大的孩子（以下简称为「大孩子」）身高之间的关系（在两者性别相同的情况下）。

根据我们之前已经学过的知识，我们可以建立一个简单的线性回归模型：

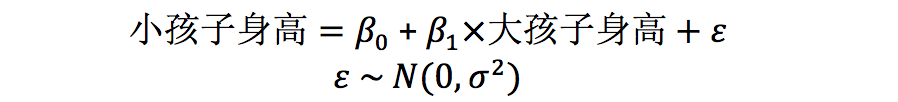
使用统计学软件在数据上拟合这个模型，我们会得到

	估计值	t 值	p 值	95% 置信区间
截距	80.82	5.16	4.59e-06	[49.36, 112.29]
大孩子身高的回归系数 β₁	0.31	2.67	0.010	[0.077, 0.549]

换言之，根据这个模型，同一个家庭中两个孩子的身高的关系是

小孩子身高 ~ 80.82 + 0.31 x 大孩子身高

而且，我们观察「大孩子身高」这个自变量的回归系数 β₁的估计值、p 值及其置信区间，可以判断出两个孩子的身高有显著的正相关关系。

根据数据画出如下图形，也能印证这一点。

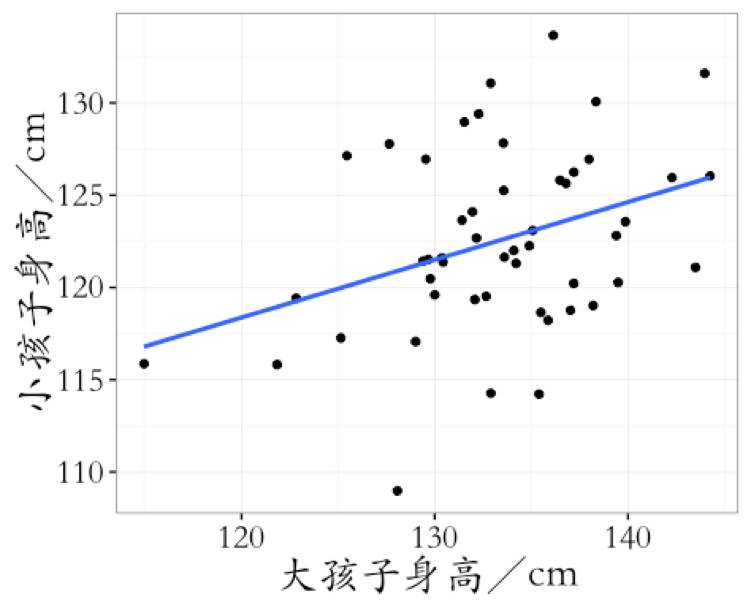
然而，故事到这里还没有结束。

在前两集文章里，我们已经知道，孩子的身高与父母平均身高是有显著关系的。现在虽然是不一样的数据集，还有大、小孩子之分，但按道理来说，这一条应该仍然适用才对。的确，如果我们拿大、小孩子身高做因变量，父母平均身高做自变量，分别做个线性回归，就能确认这一点：

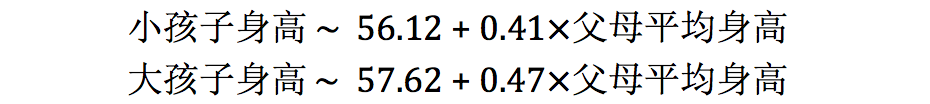
而且，父母平均身高在这两个模型的回归系数 0.41 和 0.47 对应的 p 值都远小于 0.001，因此这一关系也具有统计学显著性。

这时，如果我们把这一结果和前面得到的小孩子与大孩子身高之间的正相关关系放在一起考虑，就会产生一个疑问：大、小孩子身高之间的关系会不会只是体现了它们各自与父母平均身高的关系？换句话说，在模型

小孩子身高 ~ 80.82 + 0.31 x 大孩子身高

里，大孩子身高会不会只是充当了父母平均身高的「代理人」的角色？

要解开这个疑问，我们就得看看大孩子身高是否在父母平均身高之上还有额外的、与小孩子身高的相关性。也就是说：

假定我们已经知道了父母平均身高，进一步了解大孩子身高是否会让我们对小孩子身高的估计更准确？

因此，我们就要把大孩子身高和父母平均身高同时放到一个回归模型中，进行多重线性回归分析：

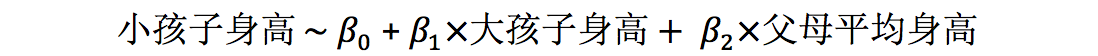
	估计值	t 值	p 值	95% 置信区间
截距 β₀	54.25	3.52	0.0010	[23.22, 85.27]
大孩子身高的回归系数 β₁	0.03	0.26	0.798	［-0.22, 0.28]
父母平均身高的回归系数 β₂	0.40	3.85	0.0004	[0.19, 0.61]

检查上面的结果，我们立刻可以看到，在这个模型里，父母平均身高依然有显著大于 0 的回归系数，而大孩子身高的回归系数和 0 并没有显著区别。

还记得我们之前反复强调过的、有多个自变量时回归系数的意义吗？这个结果的意思是说，在给定父母平均身高时，大孩子身高与小孩子身高之间并没有显著的相关关系。换句话说，要预测某个有两个孩子的家庭中小孩子的身高，如果我们已经知道了父母平均身高，再知道大孩子身高并不会对我们有什么帮助。

很显然，比较

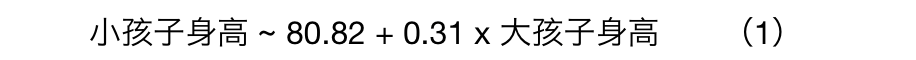
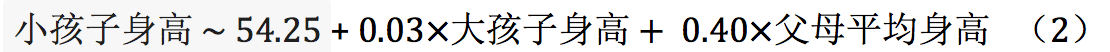
这两个模型，对于小孩子身高与大孩子身高之间的关系，我们会得到很不一样的结论。究其原因，就在于在模型（1）中，大、小孩子身高之间的正相关关系只是一种表象，它的背后推手其实是小孩子身高与父母平均身高之间的相关性。

由于在模型（1）里，父母平均身高藏在了幕后，于是大孩子身高才成了「替罪羊」，把原本属于父母平均身高的相关性拿到了自己头上。在统计学上，这种现象时常被称为「虚假关联」（spurious association）。

而在模型（2）中，父母平均身高被推向了前台，它和小孩子身高的关联性才算是大白于天下。而此时我们才能发现，小孩子身高的大或小，其实并没有大孩子身高什么事儿。

回到我们最初的目的——探究同一家庭的兄弟或姐妹两人身高之间的联系，我们应该学到什么？

在这个例子里，父母平均身高本身并不是我们想要研究的问题，然而由于它对大孩子、小孩子身高这两个变量的共同影响，使得在只分析后两者时，产生了有偏差的解读。这种情况下，虚假关联的制造者——父母平均身高——被称为混杂变量（confound variable，或 confounding variable）。

要去除混杂变量的影响，我们就要通过多重线性回归的方法，把来自父母平均身高的相关性排除掉，这样才能找到我们感兴趣的变量之间更真实的关联。所以呢，即便有些时候我们只对一个自变量感兴趣，还是得把多重线性回归这个工具用好，才能把数据背后的故事看得更清楚呢！

许多时候，虚假关联能够很好地解释一些让人莫名其妙的统计学结果。

一个著名的案例就是，许多温带或亚热带国家冰激淋的销量和公共泳池中溺死的人数之间有十分显著的正相关关系。但是这两者之间真有什么直接联系吗？我们很容易想到，其实是季节变换在背后作祟——夏天天气变热，冰激淋销量大大增加，与此同时泳池的使用者也在增多，进而也会有更多的事故。就像我们的例子那样，忽略了气温或季节这个混杂变量，我们就容易得到荒诞的结论。

当然了，这样说来难免有些轻巧，事实上，要判断清楚什么变量可能会是混杂变量，是一件很需要洞察力的事情。在许多科研问题中，我们感兴趣的自变量可能有若干个，每个自变量与因变量之间的关系又可能对应若干个潜在的混杂变量。

所以，一种普遍的做法，就是像我们前面的例子一样，把可能的混杂变量包含在统计模型中，这样我们才能更有信心地认为，观察到的有潜在科学意义的发现不会是虚假关联。

但是，有限的科研资源和样本量往往不容许我们测量或控制一切变量，或是把什么变量都一股脑往模型里扔。因此，我们还要对具体科研问题有深入的认识，并以此为指导做好实验设计、数据收集工作，尽可能有的放矢。我们今后还会继续和大家一起探讨这些技巧和方法。

最后，我们还要强调一个容易让人产生误解的问题：

在前面的例子里，没有包含「混杂变量」的模型（比如说小孩子身高与大孩子身高相关、冰激淋销量与溺死人数相关等）本身并不是「错误」的。

这些显著的相关关系在数值上是真实存在的。纯粹从预测的角度看，如果我们不知道父母平均身高，用大孩子身高来预测小孩子身高的确是最合理的办法。

它的问题在于，如果我们认为两者之间存在机制性的、甚至是具有因果关系的联系，那么就可能要犯错误了——如果你想减少泳池的安全事故，不去改进泳池的设计、多安排几个救生员、多对人们进行警示教育，却要禁止冰激淋的销售，那恐怕是得不到你想要的效果的。

正如我们反复讨论过的，线性回归本身不能提供因果性的结论，它只能对变量之间的相关性进行检验和推断。

事实上，包含了父母平均身高的模型在没有其他知识或实验研究的支持下，也不见得就是「正确」的——会不会还有别的「混杂变量」，导致孩子身高与父母平均身高的相关性也是一种虚假关联？这在理论上并非不可能。我们只能说，它提供了大、小孩子身高之间相关性的一种更合乎数据和常理的解释而已。

END

点击下方标题可阅读本系列任意文章