在Logistic回归分析时,为了验证我们分析结果的重要,高分杂志往往会要求作者将变量变换着形式进入模型,看能否得到一致的结果,以充分证明分析的可靠。
而具体变化的规则,就是松哥反复强调的,从高级变低级。(即计量-等级-计数);而建模策略请大家参考松哥的:
此文将颠覆你对多因素分析建模策略的认识【松哥漫谈】
如果分析得到的规律是真实存在的,那么同一变量的不同形式得到的结果应该是一致的。就像你真爱她的话,不会因为时间改变了她的容颜,而产生变化。如果发生变化,说明你并不是真真正正的爱(有点酸,打住!)
有人进行了一次Logistic回归,研究年龄(age),性别(sex)和体质指数(BMI)对某种疾病(Y)的关系研究,然而发生了一件不想发生的事情!
3个自变量,年龄(age)为计量资料的形式;性别为(0、1)二分类变量;BMI根据专业,设定为等级(1=营养不良,2=正常,3=超重)。【
这样设置用心良苦,因为3个变量,老大、老二和老三都到了
】,效应量(Y)为某种疾病(0=无病,1=有病)。
根据上述数据说明,与分析目的,应该采用二项Logistic回归进行风险因素发现是没问题的。于是原作者就进行了二项Logistic回归,得到结果如下:
(1)注:此时年龄为连续变量进入模型
大家可见,三个变量只有age有意义,OR=1.019,95%CI:1.001-1.038;其他两个变量无统计学意义。
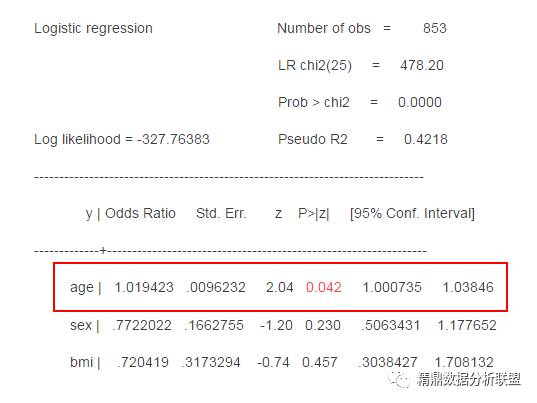
到此时,貌似没有任何问题。为了验证age是不是真正的与疾病(Y)有关,于是原作者将age计量资料(连续性资料)转化为等级资料,然后加入模型进行分析。结果如下:
(2)把age每隔10年一变后
,(即2=20-39岁,3=30-39岁...)
结果发现,年龄等级分组后(ageage),竟然没有意义了!!这到底是为什么呢?


所谓“偏听则暗 兼听则明”,本例如果age真的与疾病Y有关联,是其危险因素,那么当age以计量资料进入是,得到结果解释为年龄每增加1岁,发生该病的风险增加0.019,即1.9%,(P<0.05)。
然而大家试想一下,很多的时候,某种疾病的发生并不是年龄增加1岁就有多大的变化。因此我们才考虑将age(计量资料)转化为等级资料,如本例以10岁为一个等级进行分组。即文中ageage变量。
可是分析结果发现,ageage变量却没有意义了。那年龄到底与该疾病有无关系呢?
-
基于本例研究的数据,应该年龄与该疾病有关系的证据不做。理论上,如果计量资料的形式P<0.05,那么换成等级资料的形式,P应该肯定小于0.05才对。因为换成等级,解释为每增加1个等级的发病风险,此时1个等级为10岁,发病风险应该增大才对。
-
为什么很多高质量论文,将计量资料进入模型分析,然后再转换为等级放入模型再分析,也就是对规律的再次证实。
-
那么本例为什么计量资料分析时,P<0.05了呢?大家细看,你会发现,此时的OR的95%可信区间也就仅仅比1大那么一点点点!而且可信区间很窄,说明啥,说明本例样本量比较大。按照3个自变量的Logistic回归,大约60例样本就够了,而本例有多少?有853例,很可能因为样本量过大导致的哦!所谓“
样本过大易过溢,样本过小不识别
”。
-
本例上述松哥进行推断辨析的基础,是按照正规正常程序进行的回归。如果自变量未经线性识别,而呈现其他U型,曲线,或者啥阈值效应或积累效应等,不包括哦!
关系型分析是统计分析的最高境界,各种原因、各种现象需要一定的统计学思维进行辨析。对于初学者,或者想提升的入门者,学习统计最佳的捷径,就是跟人学,别指望自学成才,国内统计书上的理论,太过于简单,现实中遇到问题翻书,往往是找不到答案的。所谓“书到用时找不到”。同时国内统计授课或者传播的水平相比国外发达国家,还是要落后10年,都不为过!我辈努力吧!






