本文版权属于讲座人@frazer和未名湖的鱼群
主讲人简介:77年大学工科,之前知青2年。1986纽约州立大学MBA。做过若干杂事,现退休在亚利桑那州凤凰城陪家人。喜旅游和杂读。
谢谢各位光临,今天的讲座想介绍一下复杂性理论和混沌理论。原想一并讲讲演化理论,因为和复杂性理论密切相关,但看来野心过大,只能以后再说了。
首先想说明的一点是,复杂性理论和混沌理论均发端于自然科学,其理论陈述自然离不开自然科学术语和公式,毕竟一种理论无法独立于构成它的术语系统。不过今天讲座的目的是科普,是介绍一种不同于决定论的新思维方式,着眼点是如何增进我们对生活和历史的理解而非阐述整个复杂性科学,所以力求简洁和通俗。
今天的讲座如果能达到以下效果我就非常满足了:牛顿式的决定论思维方式只是我们对真实世界的一种简单抽象,一旦进入真实世界,我们需要转向一种新的思维方式。
定义复杂系统并不容易。即便是在学界,对它的定义也五花八门。不过,我们可以先把定义放一边,先不说什么是复杂系统 ,而是反过来说说什么不是复杂系统。
一个容易望文生义的理解是:复杂系统就是系统很复杂,不容易被我们一眼看清和了解,比如手表表芯的机械齿轮系统很复杂,电脑的线路板很复杂,天体的分布和运行系统很复杂,或者一个有100个变量的线性联立方程很复杂。没错,这些系统都很复杂,但它们都不是复杂系统。它们最多能被称为复杂的简单系统。
什么是简单系统呢?其实说清什么是简单系统也不简单。 其实我们看看大自然中,你能看到的东西都不简单,天上的云,河里的水,草原上奔腾的动物和生长的植物,夏天的风,冬天的雪,春天的雷,秋天的果实。这些东西,你可以感觉,可以用诗歌去描写,可以用画来描绘,但是对于云,你可以有1000种方式去讴歌,也可以有1000种方式去描绘,但你却无法明确无误地说清什么是云,比如你永远也无法准确描绘云的形状和它运动的方式。它的无穷丰富性使得你的任何描述都相形见绌。
为了能够描述自然并从纷乱的现象界中理出个头绪,希腊哲学家想了不少办法。
一个办法是企图把看似没有规则的现象规则化。现象虽然很杂,但它背后是不是有什么不变形呢?柏拉图就是这个路数。他对现象就很不满意,他认为现象不过是理念在现实世界中的投影罢了。也就是说,你别看现象界如此复杂和纷乱,但它们的背后都有一个确定不变的理念或形式。比如你不要看圆的种类很多,有大有小,而且现实中的圆都是不规则的,但背后的理念是围绕某个定点做等距运动的轨迹。他说现象中的马有多种,但背后这个”马“的理念只有一个。有了这个理念,你就可以在现象界看到各式各样的圆和各式各样的马,多样性就变得单一了,”本质“被找到了,不确定也就变得确定了。
柏拉图的宇宙观设想宇宙初始有两种直角三角形,由它们可以产生四种正多面体,这4种正多面体就是四大元素,对应于自然界的火、气、水、和土,即火是正四面体,气是正八面体,水是正二十面体,土是立方体。还有个由正五边形构成的十二面体,叫以太。这么一来,世界万物的描述就被归纳成这些简单要素的组合了,变成简单的几何学运算了,这听上去是不是很High?
希腊人解释世界的另一个努力叫”理性“。理性这个词在英文中叫Ration,也是几何学中比例的意思。也就是说,理性是万物之间一种合乎比例的关系,像几何学那样。
理性主义的鼻祖应该算是毕达哥拉斯(公元前570–495),就是那个证明勾股定理的数学家。他的名言是”万物皆数“,不仅是直角三角形中斜边和另外两条边之间要满足一定的比例关系,而且琴弦的长度和音高之间也要符合某种比例关系。意思是说,所有看到听到的现象都是虚幻的,只有它们之间的几何或数字关系才是真实的。
他之后的柏拉图当然也是理性主义的鼻祖之一,他崇尚理性和推理,特别是几何学,他对不懂几何学的人是极为歧视的,所以在他的柏拉图学园的大门口挂了块牌子说“不懂几何学者不得入内”!
不论是理念还是理性,都是对自然的一种抽象,企图化复杂为简单,即把复杂性和不确定性降低到我们有限的大脑可以把握、理解、描述和计算的东西。
理性主义导向决定论:既然世界是客观的,而事物之间又存在因果关系,那么世界就是可以由因果关系由近及远将所有一切都纳入这张因果的大网之中,或者说,世界可以从理性推导出来。虽然推导需要时间,但最终理性的光明会照亮所有的黑暗之处,进步是历史的必然,世界一片光明。
笛卡儿(1596年-1650年) 是欧陆理性主义之父。他认为,凡是在理性看来清楚明白的就是“真”的。复杂的事情看不明白,应当把它尽可能分成简单的部分,直到理性可以看清其真伪的程度。他认为动物是可以约化还原成自动机(Automaton),或称机器人偶:
很明显,在笛卡尔这里,生命本身都是可以约化为机械零件并按照图纸重新构建起来的。
还有几位大名鼎鼎的哲学家也说过类似的话:
康德(1724年-1804)说,一切历史现象、历史事件,包括人们的道德选择,完全由理性为道德行为颁布的道德律令所决定。
孟德斯鸠(1689年-1755年)说:“人,作为一个‘物理的存在物’来说,是和一切物体一样,受不变的规律支配。”
荷兰的斯宾诺莎(1632-1677)认为偶然性只是人类认识的无知造成的
不要说,这种思维方式还真的很成功,延续到近代,的确推动了现代自然科学的发展并获得巨大成功。人类在数学、物理、化学、宇宙学方面获得的成就可以说在很大程度上都归功于理性主义。不论是牛顿(1643-1727)的经典力学、麦克斯韦(1831-1879)方程还是爱因斯坦的相对论,应该说都是理性主义的胜利的证明。
牛顿爵士的墓志铭上写着的,“他几乎神一般的思维力,最先说明 了行星的运动和图像、彗星的轨道和大海的潮汐“。似乎宇宙中任何运动物体如果质量已知、外力给定,给定初始位置,那么它在任意时刻的空间位置就可被牛顿定律所确定。
这种理性主义的数学表达形式就是著名的哈密顿方程:
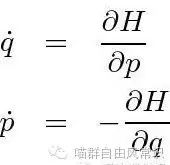
其中,P是物体的动量,q是位置,H是哈密尔顿算符。使用这个方程,就可以在高维相空间中确定任意时刻一个物体的动量和位置,或者说,去预言一个物体的历史。如果这个物体是一个点,那么这个方程可以描述这个点的一条历史曲线,如果这个点的初始是一个不确定的区域,那么这个方程可以描述这个区域在相空间中的一个历史“流形”。 更吓人的是,这个相空间就是宇宙本身,而这组方程涵盖了宇宙中的所有可能性和所有历史,它不仅可以预测未来,而且可以追索过去(反推历史)。它因此是超越对个别物体的描述的!
这实在是豪气冲天!
理性主义的胜利反过来形成了人类对理性主义的信仰甚至是崇拜。这种乐观主义情绪不仅成了自然科学界的主流,它而且还扩散延伸到自然科学之外几乎所有的学科,包括社会学、政治学、经济学、心理学和历史学等。
理性主义“云”包括这些词汇:

他们考虑问题应该是这样的:

从哲学上说,牛顿本体论的元素是物质,存在于绝对的时间和空间。牛顿系统是可以拆分成粒子的,而粒子不能合并、分裂、产生或消失。在牛顿系统中,并不需要引入意识、生命、组织、目的等等。
牛顿的世界没有新颖和创新,所有现存事物从来就存在,而且会一直存在下去,虽然形态会变化。对牛顿而言,科学只是发现(存在)而已,没有创造,知识只是从客体向主体转移而已。。。
理性主义的乐观在很大程度上是建立在所谓还原/约化理论之上的(Reductionist)。按照上面笛卡尔的说法,复杂的事情看不明白,应当把它尽可能分成简单的部分,直到理性可以看清其真伪的程度。也就是说,整体如果复杂的话,可以把他分解成部分,以此类推,找到最基础的构造单元,如果把部分搞清楚了,也就能把复杂的东西搞清楚了。
有个以著名法国数学家拉普拉斯命名的“拉普拉斯妖”。他在1814年提出,人的理性能知道宇宙中每個原子確切的位置和動量,能夠使用牛頓定律來展現宇宙事件的整個過程,過去以及未來。他的原话是:
“我們可以把宇宙現在的狀態視為其過去的果以及未來的因。假若一位智者會知道在某一時刻所有促使自然運動的力和所有組構自然的物體的位置,假若他也能夠對這些數據進行分析,則在宇宙裡,從最大的物體到最小的粒子,它們的運動都包含在一條簡單公式裏。對於這位智者來說,沒有任何事物會是含糊的,並且未來只會像過去般出現在他眼前。”
以宇宙生成为例,我们如果将时间反演往回推,就能把我们看到的各种冷却后能级较低尺寸较大的物质一路还原成尺寸较小和能级较高的物质,最后推到大爆炸起初的最原初物质。例如,我们可以将晶体向下为解分子、原子、原子核、质子和夸克等等。 见下图(图片来源:张广铭:《物物理学中的演生现象》
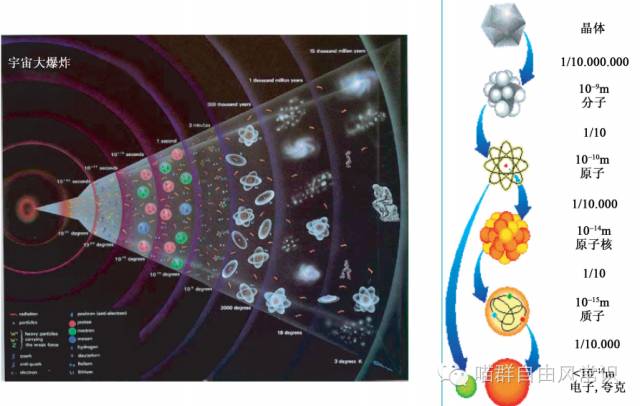
我们后面再说这个还原论有什么问题,还是先我们回过头来再看看决定论遇到了什么麻烦。
辉煌的决定论在两个方面受到了挑战,第一个挑战是19世纪末到20世纪初由普朗克、波尔、海森堡、薛定谔等物理学家创建的量子力学理论。量子力学在哲学上的意义一点不亚于它在物理学上的意义:世界不再是决定性的,例如我们只能计算粒子的概率分布而不能准确说出它的位置和动能;
世界不再是与主体无关的,而与观察者的观察方式息息相关。
世界的随机性是事物的本性而非人类认识能力的欠缺。也就是说,无论我们如何完善我们对世界的认识,世界将永远是不确定的,不确定性就是本质。
量子力学是人类20世纪最伟大的成就之一,它深刻地改变了人类对世界的认识,但今天讲座的重点不是这个。
人类恐惧无序,所以追求有序。人类在过去几百年中追求有序的努力得到了极大的回报。然而,人类的有序系统是建立在三个基本假设之上的:
1. 重要因素论
2. 线性可加论
3. 能量守恒性
第一点说的是一个系统的特性是由主要因素决定的,所以你只要找出若干主要因素就可以描述系统的特性了;小因素可以忽略不计。
第二点其实隐含两方面:一个是系统内的元素(或子系统)是独立的,相互间没有互动,第二个是整体等于部分之和,或者反过来说 ,把部分加起来就是整体;
第三点其实说的是系统是封闭的,与外界没有能量和信息交换。
可是一旦进入真实系统,我们发现上面三条假设每条都有问题。
针对以上第一点,真实系统(世界)一是变量多,维度高,往往是有几十甚至几百个变量的巨量复杂系统,二是其子系统往往是能动主体(Intelligent Agent),而不是像钟表那样的部件。
更重要的是,在巨量复杂系统中,我们已经无法确定什么是主要因素,什么是小因素。Agents之间的关系极为复杂,以至于你认为次要的的小因素往往在系统中扮演决定性的作用。
针对以上第二点,把系统分解约化为部分或子系统后,原系统的的特性便丧失了。换言之,部分之和不等于整体,正如把N个人加在一起不等于社会,把无数细胞加起来不等于人。再换言之,把每个个体的特性研究的再清楚你也导不出社会的性质,把单个细胞研究的再透彻也得不出人的性质。
反过来说,你虽然可以把系统分成子系统和子子系统,但子子系统演化形成子系统时,有些新的特性突然“涌现(Emerge)”了出来,它不属于子子系统而只属于子系统,同样,当子系统演化成上一级系统时,某些新的仅仅属于上一级系统的特性突然“涌现”了出来,它们并不属于子系统。例如,氯化钠(盐)由金属钠和氯气构成,但前者强反应,后者是有毒气体,但盐不仅可食,而且有咸味。
所以,把系统分成子系统这件事是需要特别特别小心的,对于无生命的机械系统你或许可以如此操作,但一旦牵涉到复杂系统(不必是生命系统)时,你需要特别清醒地认识这种操作的局限和问题。
线性可加的另一个前提是所谓“连续可微”。撇开数学证明直观地看,连续性是预测的基本要求,如果事件之间根本是不连续的,你如何能够预测点运动的下一刻行为?除了连续之外,点运动的变化率也必须是连续的(可导),如果一个点的运动方向呈不规则运动,你如何能够预测?可是在真实世界中,部分之间未必有连续性,其变化方向就更不一定有连续性。
非线性的另一层含义研究输入和输出之间的关系,或者说研究每个因素对系统的影响大小。Agent之间的相互作用以及对系统的影响可以非常复杂,可能是几何关系,也可能是高阶几何关系。这样一来,因此,对系统真正有影响的变量不是那些在输入端看上去数值大的量,而是那些看上去也许数值不大,但控制了”关键关系“的变量,或者说决定了”系统路径“的变量。
这样一来,一个高维非线性系统对于初始状态的微小变化将是极端敏感的。这个我们在后面介绍混沌理论时会进一步讨论。
系统非线性的最后一个含义涉及系统的反馈性。 在一个各变量相互关联的系统中,此一刻的输出就构成下一刻的输入,如此迭代循环。反馈关系可以是负反馈,也可以是正反馈。如果输出值根据系统的某个吸引子所要求的值调节输入值(围绕吸引子值而增加或减小),那么这就是所谓负反馈,因此也形成一个稳定系统,也就是说,系统会补偿来自环境的扰动造成的偏离理想状态的力量。
如果输出值缺乏这样一种调节功能而与输入值形成你追我赶的局面,那么这就是正反馈,这会使系统迅速朝某个方向狂奔,直至崩溃(中性意义上的崩溃,可以解释为组织的解体或变形)。(不妨以此来思考股市或房市)
至于能量守恒假设,真实世界中哪里有不与外界交换能量的封闭系统呢?真实系统都是耗散系统,这包括能量和信息的交换。能量守恒意味着系统将达到熵最大状态(热寂),系统的任何组织状态都将消失。
生命在于交换,在于吸收能量和信息,只有在不断的能量和信息输入下,或者说,只有当系统的能量足够高,复杂度足够高和信息足够丰富之时,系统才会具有自组织性。这一点不仅对我们认识自然系统非常重要,而且对我们认识社会和文明秩序的产生能力尤其重要。(突然想到有人死劲证明“中华文明独立演化说” :-)。
也就是说,一旦进入真实世界,原先我们做预测所依赖的全部假设都不满足了,换言之:决定论的哈密尔顿方程根本无法进入真实世界。
在真实世界中,我们看到无序无处不在:天上的云、气温的变化、湍急的水流、山川湖泊的形状、物种的变异、股票的走向等等。随机现象、不连续性和不稳定性无处不在,这些都严重挑战“世界有序”的信念。 因此,20 世纪70年代后, Complexity成了一个重要词汇涌现出来并迅速成为一种新的思想范式,以至于Stephen Hawking说: 我相信, 21 世纪将是复杂性的世纪。
1984年,原先一帮在美国新墨西哥州Las Alomos原子弹基地工作的顶尖物理学家在新墨西哥州首府Santa Fe成立一个专门研究复杂性的机构,其创始人有 George Cowan, David Pines, Stirling Colgate , Murray Gell-Mann (获1969年诺贝尔物理学奖), Nick Metropolis, Herb Anderson, Peter A. Carruthers, and Richard Slansky。其研究人员采取访问学者制,许多顶级科学家和经济学家都在此做过研究,如Kenneth Arrow(经济学家,1972年诺贝尔经济学奖获得者)。
1987年该研究所召开了美国首届复杂性科学学术会议,复杂性研究从此如雨后春笋般生长起来。他们的研究课题十分广泛,涉及:
地球上出现生命之前的化学演化和之后的生物演化
哺乳动物的免疫系统理论
人类与动物个体的学习和思维
人类文化和语言的演变
全球经济作为复杂的演化系统
计算机和程序设计的全新战略
等等
如下图所示,复杂科学是一门高度综合性的理论,它涉及的领域包括:博弈论、集体行为学、网络理论、进化适应理论、Pattern的形成、系统论、非线性动力学、自组织理论、涌现理论等等。
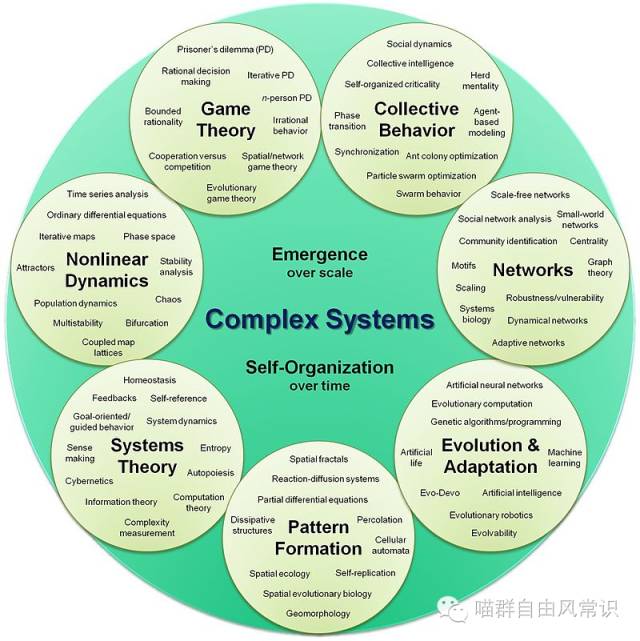
复杂适应系统的模型大致是这样的:
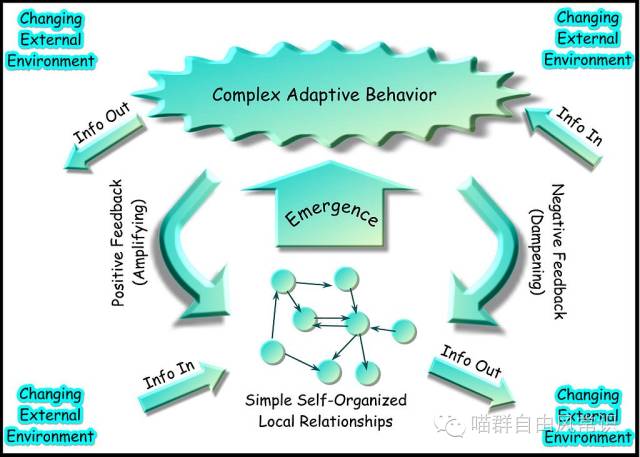
可以看到,这样一个系统首先存在于一个变化的环境之中,它的中心是根据本地关系和原则形成的自组织体,自组织会涌现出系统的新性质,这些性质决定了系统所具有的环境适应行为。系统本身及其子系统和与外界有不断的信息交换(流入和流出),并通过正、负反馈系统在系统和子系统之间实现系统耦合。
复杂系统理论的一个重要组成部分是混沌理论。系统的复杂性有相当大一部分来自高维系统(具有多个变量)固有的混沌性质。那么究竟什么是混沌或混沌理论呢?
简单地说,混沌是一种介于有序和无序之间的中间状态。 根据维基定义:混沌理论是数学研究的一支,研究对初始条件极为敏感的动态系统的特性,即研究那种俗称为“蝴蝶效应”的现象。
1963年麻省理工气象学家爱德华-洛伦兹为了研究气象学中的热对流问题,建立了这样一组偏微分方程:((故事细节请自己上网查看))

这个方程仅有三个变量,看似简单。但就是这么简单的一个方程居然无法给出确定解。尤其重要的是,哪怕你对输入值(初始值)做微小改变(如小数点后5位),系统的解就可能发生巨大偏差,无法给出确定或收敛的解。解的轨迹在相空间中随机地沿着一个蝴蝶形行走,像这样:

上面这个图像是一团麻线,有个小飞虫在里边随机飞行,但永远不与飞过的路径相交。这是一个有序和无序完美结合在一起的例子。小虫的飞行路径虽然是随机而不可确定的,但你可以非常确定地知道它绝对飞不出这只蝴蝶,在此意义上,这个蝴蝶就是一个”吸引子“,或者说像是一个蝴蝶形的势阱,小虫子无论如何努力和乱窜,也不可能飞出这个势阱。
所谓“吸引子”就是一种平衡态。一个系统可以有多个吸引子(多种平衡态),但每一种平衡态的稳定性是不同的,系统进入每一种平衡态的概率大小也是不同的。 比如把一根筷子竖着放在桌子上是一种平衡态,把它躺着放在桌子上也是一种平衡态,但显然前者是不稳定的平衡,而后者是稳定的平衡。
他把这种对小扰动对系统造成的巨大影响形象地比喻成 “蝴蝶效应”。洛仑兹的问题是:一只蝴蝶在巴西扇动翅膀会在得克萨斯引起龙卷风吗?
西方有这样一首民谣,说的也是这个意思:
钉子缺,蹄铁卸;
蹄铁卸,战马蹶;
战马蹶,骑士绝;
骑士绝,战事折;
战事折,国家灭。
可以直观地看到,系统的稳定性与系统所处的能量状态有关,显然,势能越小越稳定,这也是为什么倒下的筷子比站立的筷子要稳定的原因。自然的状态一般都是系统势能最小的状态,系统追求自然,应该算是一种本能吧?扭曲的系统往往不稳定,因为扭曲的系统非自然,不符合自然本性。
系统的稳定性(或曰“鲁棒性” Robustness)也可以从另一个角度来看,即当你给系统一个扰动时,看它是不是还能够保持平衡,也就是说,看它是否对初始状态敏感。 对以上第一种情形,很容易知道,给筷子施加一个微小的力,筷子就会倒下,脱离平衡状态;而后一种情形,你给它施加一个大的力,筷子仍然还会躺在那里。所以,第一种平衡是不稳定的平衡,而后一种是稳定的平衡。
所以鲁棒性可以用来衡量一个系统抗干扰的能力(健康的状态)。当一个社会全力维稳时,其鲁棒性肯定是极低的(极不健康的?),系统的这种性质也叫“脆弱性” (Fragility)。
系统具有稳定性(存在“吸引子”)是因为系统存在反馈机制,例如冰箱把温度(一个变量)控制5度上,是因为有个恒温器,只要它测到输出变量偏离了5度,马上就会调节输入变量,使得输出值回到5度上。也就是说,一维系统的吸引子就是一个数值。
又如一个挂钟的种摆,如果不考虑它的质量和损耗(理想单摆系统),它有两个变量(振幅和角频率),那么它的稳态就不是一个值了,而是按周期周而复始地摆动。或者说,一个二维系统的吸引子就是一个重复的周期运动。周期运动无处不在,心跳、呼吸、潮汐、四季变化等等……
一维和二维的系统都是简单系统,不会出现上面所说的混沌现象,但一旦变量变成三个或三个以上,情况就不同了。例如上面所说的具有三个变量的洛伦兹方程。高纬度有点类似高自由度,低自由度下,个体的选择非常小,行为简单,产生不出混沌,也不可能产生组织和新结构,而在高维度下,个体的选择自由度提高,就会出现复杂行为,只有在这样的行为主体和环境下,才会出现混沌现象和产生自组织。
James Gleick 的《混沌》这本书讲述了混沌理论的诞生故事,其中有张图如下,描述了系统的四种行为:
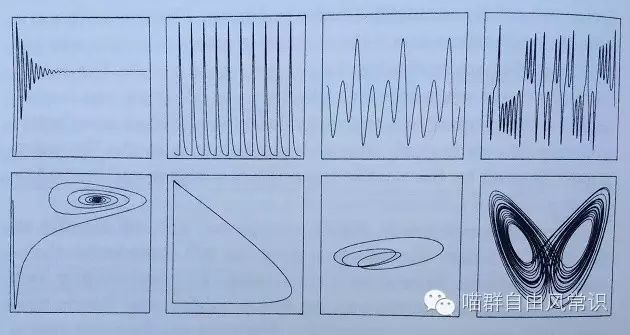
这张图的上面四张是用传统的时间序列方式来描述,下面四张是用“相空间”的方式来描述,其实都是描述一个复杂系统的四种可能状态。
最左边的那个,在时间序列中收敛于一条线,在相空间中收敛于一个定点(比如5度)
第二张,在时间序列里呈规则振荡,在相空间中收敛于一个闭环,(比如钟摆的规则摆动)
第三张,不收敛,处于无序状态,被称为“周期三” (参考: Period Three Implies Chaos http://www.its.caltech.edu/~matilde/LiYorke.pdf)这是一个孕育混沌的状态。
第四张,馄饨态,洛伦兹蝴蝶,在“奇异吸引子”的作用下,产生的新结构/组织
所谓“奇异吸引子”是指一个动力系统的解曲线最终被一个混乱的吸引子吸去了。也就是说,若我们跟随这些曲线走,最后会趋近于一团混乱的状 态,毫无规则可寻。
有意思的是,我们可以从无序的海洋里产生结构,这是自组织的结果。混沌并不是完全的无序,它介于有序和无序之间。非线性虽然会产生不可预测性,但也会产生新的结构和组织,正如一个复杂的系统会产生湍流和凝聚,一个决定性的系统产生的不仅仅是周期性行为,这就是“稳定的混沌”的含义。 (再想想“崩溃论”有那么可怕吗?)
这和道家的 “道生一,一生二,三生万物” 有点神似啊!
洛伦兹从中受到的启发是: 高维系统本质上是不可能做长程预测的,哪怕系统本身是决定性的而无随机因素,而且对初始条件高度敏感。换言之,系统的决定论性质并不能保证系统的行为是可以预测的。 这种行为也被称为“决定性的混沌”。
如果小因素在复杂系统中不可忽视,那么系统所受到的随机扰动也就不能忽视,这样就把随机性引入了复杂系统。特别是当系统临近节点时,系统变得高度不稳定,随机扰动和小事件往往扮演决定性作用。比如当系统高度不稳定时,一个极小的城管和小贩之间的纠纷可以演变为一场涉及数万人的“恶性”群体事件。
混沌现象的发现与建立与相对论、量子力学一起被一些科学 家们誉称为二十世纪物理学上的三大革命。 从20世纪80年代中期到20世纪末,混沌理论迅速吸引了数学、物理、工程、生态学、经济学、气象学、情报学等诸多领域学者有关注,引发了全球混沌热。
混沌这门学科的第一次国际会议 1977 年颇具意义地在文艺复兴时代的发源地意大利召开。大会组织者之一、 美国佐治亚理工学院的物理学家福特 (Joseph Ford, 1927-1995) 说: “相对论除去了绝对空间与时间的幻想,量子力学清除了可控测量过程 的牛顿梦,而混沌学则宣告了拉普拉斯决定论式可预测性的幻灭。”
美国作家James Gleick 在1987年出版的畅销书《混沌》的序言中说:“混沌开始之处,就是经典科学终止之时。
在以上的讨论中,其实我们已经对复杂系统各方面的特征作了讨论。作为总结,我们来看看复杂性理论的一些主要特性:
1. 复杂系统具有多主体、多因素、多变量,它们之间具有复杂的交互输出、输入关系。这样一个由多主体构成的互为输出输入的系统群形成一个网络,构成一个超系统。
多主体/子系统/单元间有高度相互依赖性,子系统并不是一个个独立的单元,而是一组输入到输出的映射关系。系统间的耦合构成超系统,其中的每个系统都是受约束的,无法与其他系统独立。超系统保证各部分的协调性。
2. 在复杂系统中,组件在一定程度上独立,有一定自主性,但和其它组件发生直接或间接联系/互动,使得全域行为难以预测,尽管不是完全随机。
3. 在生物/社会的复杂适应系统中,每个单元是一个Agent(智能个体),是个自主个体,有自己的目标或价值(功利的或寻求“舒适”)。不过,复杂系统中的Agent并不需要展示智能或精神能力,Agent涵盖很广,可以是人、蚂蚁、细胞或分子,复杂科学不区分意识或物质……
4. 系统是分层级的,新层级形成时,就会”涌现“出与本层相关的新特性,而这些新特性并不是它的组成部分所具有的。对层级而言,构成它的个体性质变得不那么重要了,反而是个体之间的关系变得更重要。这种关系就是一种涌现性质,或者说是这个层级的整体性质。
5. 复杂科学的特点在于,既不是用秩序来描述,也不是用无序来研究,而是研究混沌边缘,研究如何无序的规律和无序产生组织的机制。
6. 复杂系统中的关系是非线性的,系统中的各种变量对系统的影响不是线性成比例的。小因素会有大影响,无穷多的小因素使得复杂系统的建模几乎不可能。
7. 复杂系统不能简单拆分成部分,然后再由部分构成。整体永远大于部分。复杂科学仍然保留分析,但更强调综合。
8. 复杂系统具有开放性,与外界有能量/信息的频繁交换。系统的输入和输出,输入和输出也是连接和耦合其他系统的方式,一个系统的输出可以是另一个系统的输入。
9. 系统产生新秩序的能力与系统的信息度和复杂度有关。系统越是开放,越是能够处理高复杂度,发生变异和产生新秩序的能力就越强。(如历史上的西亚和欧洲)
10. 复杂系统理论不仅是门新科学方法,而且是一种不同的世界观和思考自然、社会和历史的方法,它让我们一方面避免简单的机械式思维,又让我们在面对无序时保持冷静和乐观。
如讲座开头所言,复杂科学、混沌理论、演化理论内容庞杂,新概念很多,在短短几十分钟的讲座中最多只能触及皮毛。本来计划介绍的演化理论(和复杂系统高度相关,互相补充)也因时间所限而放弃。本讲座只是希望通过这样一个简单介绍,激发有心人的兴趣。如果各位有兴趣了解演化理论,本人愿意再谈。
问:复杂系统 如何 合理地分层级? 层级之间的规律是否向下包含?
答:层级是自发演化出来的,只要给予复杂系统足够的维度和能量
问:最自然的状态通常是最稳定的状态,一粒豌豆在碗里,它总是会在势能最低处(碗底)。这一科学原理放在我们的社会结构里去理解。最符合人性的,也是最自然的结构,应该是最稳定的社会结构。如果违反人的本性的社会结构,那就是危险的不稳定的结构。换言之,越是要拼命维持稳定的社会结构,那一定就是最危险的社会结构,也是最不符合人性的社会结构。
答:线性是对真实世界的简化,让小脑袋舒适些。
问:"演化"是新的神吗?
答:演化是可以分析的,今天没有讲。
问:既然都是变量,充满不可知性,对现实有什么意义?难道只告诉我们“车不定开到哪里,你系好安全带就好”??!谢谢!
答: 混沌并不是完全无序,看总结的第10条。
问:爱因斯坦相对论,有什么意义?谢谢!
答:爱因斯坦的相对论,破除绝对时间神话。
问:能简单剧透下演化的源头是什么吗?
答:我接受有个自然神,创世意义上的,创完后离开了,丢下世界自我演化。
问:神留下的规律/演化 就不能再有超越性了,人也是只是这样的"机械" 产品? 有些悲观的味道。
答:不机械啊,有偶然性/随机性就有希望。
问:超越属于涌现之一种?
答:这个不是。主要是路径、节点、概率、锁定、遗传密码。
问:混沌现象的发现与建立与相对论、量子力学一起被一些科学 家们誉称为二十世纪物理学上的三大革命。 从20世纪80年代中期到20世纪末,混沌理论迅速吸引了数学、物理、工程、生态学、经济学、气象学、情报学等诸多领域学者有关注,引发了全球混沌热。这些学科的分工是来自于感性还是理性呢?谢谢!
答:问题有问题。复杂系统理论不是理性的反面,而是关注理性的不足和反对理性神话。
问:随机不可知怎么肯定这个神就不再随时随意参与甚至捣乱呢?
答:这个是信仰层面,复杂性理论就不证明了。
问:Reductionist,是指简约的方法。但是在个人与社会的关系分析上,也沿用得很多。请问:能否说明它们的来历,并做出更好的适应性的评判?谢谢!
答:所有的理性抽象或概言都是有问题的,但不一定不适用。
问:祂又是怎么演化来的呢?
答:可以开一次哲学/神学讲座。
问:祂又是怎么演化来的呢?
答:实用















