前文
如何提高期权隐波的预测准确率?(上)
介绍了第一篇文章,对隐波期限结构进行建模。本文继续为大家介绍另外两篇相关文章,都建立在之前的Nelson-Siegel 模型的基础上,但在预测上更全面更深入。
第二篇文章《Are There Gains from Modeling the Term Structure of Option Implied Volatilities?》直接回答期权隐波的期限结构是否能够被预测的问题。在介绍具体的做法和结果之前,我先回答一个读者普遍会问的问题:
为什么不预测期权价格或者回报率,而是预测隐波?
首先,隐波是业界普遍采用的报价手段,预测隐波更符合市场实际习惯。其次,隐波与期权价格是一对一的对应关系。但有人会说,你虽然能够预测隐波,但未来的现货价格你还是不知道,这样一对一的关系在预测上就不成立。这个说法当然有道理,但是我们这篇文章主要关心的是隐波对期权德尔塔中性策略的意义,因此未来现货价格如何变动对这篇文章而言是无关紧要的。只要能够预测隐波,德尔塔中性策略的经济收益就有意义。
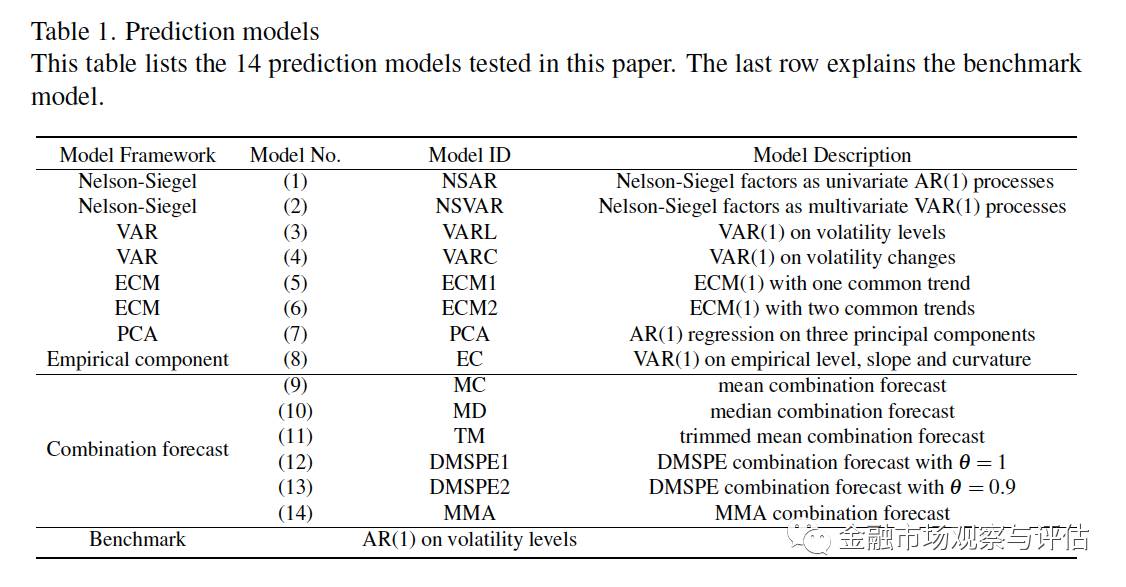
现在我们来对隐波进行预测。为此,我们比较了14个预测模型。由于篇幅所限,这里不一一列举出来。感兴趣的读者可以问我要原文。基本上前两个模型使用了第一篇文章中的 Nelson-Siegel 模型,对模型参数(beta)的预测分别采用 AR(1) 和 VAR(1) 的设定;第3和第4个模型分别对隐波的水平和变化量进行VAR(1) 建模;第5个和第6个模型都是误差修正模型 ECM, 一个考虑了单一趋势,另一个考虑了两个趋势项;第7个模型对隐波时间序列中提取的主成分进行AR(1) 建模;第8个模型对隐波的实际水平、斜度和曲度进行AR(1)建模;第9到第14个模型对以上8个模型进行不同程度的混合。最后,我们用隐波的AR(1) 模型作为基准模型,与这14个模型进行对比。
我们采用美国1996年至2015年标普500指数期权作为数据样本。样本外预测的结果显示:第一,凡是采用VAR(1)结构的模型,预测效果都普遍好于其对应的AR(1)模型,这说明
要提高某一合约隐波的预测准确率,就应该利用好隐波期限结构上的其他隐波所包含的信息
;第二,在所有的测试中,无论是对1天之后或者5天之后隐波的预测,总有10个左右的模型能够在统计上显著优于基准模型。其中模型4和一些组合模型的效果最佳。模型4对隐波的“变化量”进行建模,而不是对隐波的“绝对水平”建模,这表明
虽然同样利用了整个期限结构的信息,但如何利用这些信息建模在预测效果上还是有很大区别的
; 第三,第一篇文章中介绍的 Nelson-Siegel 模型虽然在样本内拟合表现很好,也能优于随机游走模型,但在样本外预测效果上并不如其他模型;第四,在考虑20天之后隐波的预测中,没有任何一个模型可以击败基准模型。这说明期权隐波的预测效果仅仅局限在一周以内,换句话说,期权市场在5个交易日内是市场无效的。
下图为最好的预测模型(模型4)相对于基准模型的预测误差时间序列。负值代表预测误差小于基准模型。可以看到(复制到微信后比较模糊),负值占了绝大多数的情况。
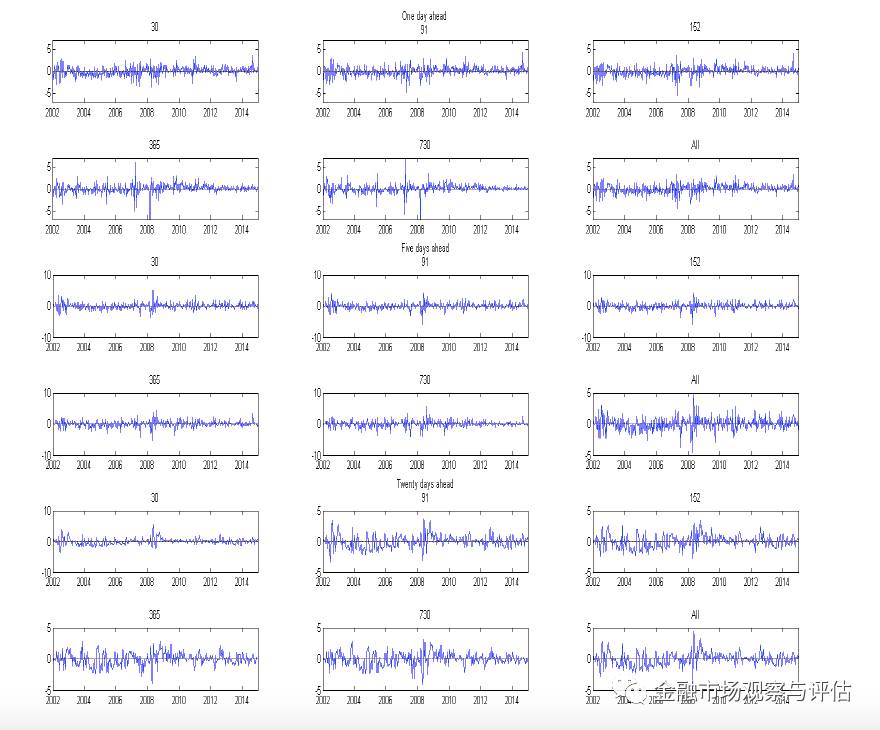
接着我们探讨这些预测统计结果能否真正用于交易策略上并产生经济效益。为此,我们根据这14个模型的预测信号构建了德尔塔中性策略,并计算 Leland's alpha 作为策略经济效益的衡量标准。结果显示,统计预测效果好的模型同样能产生较好的经济效益,而且跟上面的统计结果一致,1-5天内的经济效益非常显著优于基准模型,但在20天之后就消失了。更重要的是,这个结果并不会随交易成本而改变。我们考虑了不同的交易成本,但结论并不变。这可能是因为基准模型也同时考虑了成本,所以在对比的时候,成本这个因素互相抵消。
在文章的最后,我们当然考虑了一系列稳健性检验,比如价外期权的隐波,看跌期权的隐波,不同的经济效益衡量标准等等。这些检验的结果并没有显著改变文章的结论。
总之,这篇文章告诉我们,
要预测好隐波,就要充分利用整条期限结构的信息,而不是单单靠这个隐波的历史信息。从理论的角度看,这告诉我们,对期权建模,比如广泛使用的随机波动率模型,要考虑把波动率拆分成短期和长期两种,即所谓的波动率成分模型(Volatility Compoent Models)
。
第三篇文章《Forecasting the Term Structure of Option Implied Volatility: the Power of An Adaptive Method》将隐波的预测准确率往前更推进了一步。这篇文章里我们采用了Chen and Niu (2014, Journal of Econometrics) 中提出的 local autogression 即局部自回归(LAR)思想,将期权的隐波看成是一个随时间变化但局部稳定的时间序列,在做AR检测时自动选择最优的历史数据区间,从而达到提高预测效果的目的。
围绕这个自适应思想,我们构建了
两个自适应预测模型
。第一个是对每个单一合约隐波构建了LAR模型,第二个是对隐波的整个期限机构构建了第一篇文章中提到的Nelson-Siegel模型,但在此基础上加上了LAR预测方法。之前的第一篇和第二篇文章里面对Nelson-Siegel模型里面的三个系数只是进行了简单的AR和 VAR 处理。为便于跨模型比较,我们考虑了第二篇文章中提出的14个模型,并以随机游走模型作为基准。
实证结果是非常令人鼓舞的。虽然在第二篇文章里面,Nelson-Siegel模型的预测效果并不好,但这里我们发现,
只要采用LAR预测方法,Nelson-Siegel模型的预测效果远远优于随机游走,隐波预测的准确率可以达到60%-90%以上
。更令人振奋的是,
第二篇文章发现样本外预测只在5天内有效,但这里我们发现,只要采用LAR,样本外的预测可以延伸到20天
!之前的14个模型在进行20天预测时都不能击败随机游走,但是采用自适应性的Nelson-Siegel模型可以将预测误差降低一倍多!
介绍完了三篇文章,
读者可以带回家的信息就是:(1)隐波是完全可以预测的;(2)对隐波的预测要借助于整条期限结构的信息;(3)要进一步提高预测准确率,可以考虑采用自适应性方法
。
长按二维码关注本号






