
来源:
EDN电子技术设计
无人车作为一个复杂软硬件结合的系统,其安全可靠运行需要车载硬件、传感器集成、感知预测以及控制规划等多个模块的协同配合。本文作者认为最关键的部分是感知预测和决策控制规划的紧密配合。
狭义上的决策规划控制部分,包含了无人车行为决策(Behavior Decision)、动作规划(Motion Planning)以及反馈控制(Feedback Control)这三个模块。而从更宽泛的概念来说,无人车的决策规划控制模块,紧密依赖于上游的路由寻径(Routing)以及交通预测(Prediction)的计算结果,所以本文也对路由寻径和交通预测模块进行介绍。
系统框架和模块划分
图1展示了一种无人车软件系统的典型功能模块划分。
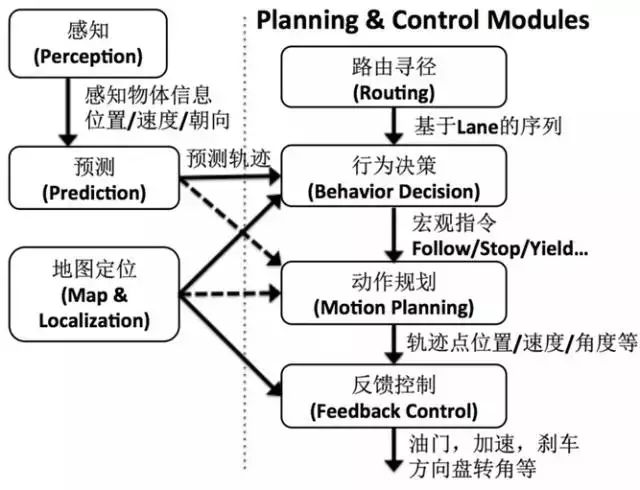
图1 无人车软件系统模块



整个决策规划控制软件系统,可以按照解决问题的不同层面,如图1所示自上而下划分为行为决策(Behavioral Decision)、动作规划(Motion Planning)以及反馈控制(Feedback Control)这三个模块。
其中行为决策模块(Decision),可以直观理解成无人车的“副驾驶”。
行为决策接受路由寻径的结果,同时也接收感知预测和地图信息。综合这些输入信息,行为决策模块在宏观上决定了无人车如何行驶。宏观层面的决策包括在道路上的正常跟车,在遇到交通灯和行人时的等待避让,以及在路口和其他车辆的交互通过等。
例如,在路由寻径要求无人车保持当前车道(Lane)行驶,感知发现前方有一辆正常行驶的车辆,行为决策的决定便很可能是跟车行为。
动作规划模块,在图1的划分中,解决的是具体的无人车动作(Motion)的规划问题。其功能可以理解为,在一个较小的时空区域内,具体解决无人车从A点到B点如何行驶的问题。
动作规划模块在这里解决的问题,相对行为决策,又更加具体了一步。动作规划需要具体把一个短暂时间t内从A到B的中间路径点做出规划,包括选择途经哪些具体的路径点,以及到达每个路径点时,无人车的速度、朝向、加速度等。



预测模块(Prediction)
作为决策规划控制模块的直接数据上游之一,预测模块的作用是对感知所探测到的物体进行行为预测,并且将预测的结果具体化为时间空间维度的轨迹传递给下游模块。
一般而言,感知模块所输出的物体信息包括位置、速度、朝向以及物体分类(如车辆,行人,自行车)等物理属性。这些感知所计算输出的物体属性偏向于客观的物理属性。利用这些输出的属性,结合客观的物理规律,可以对物体做出一个在非常短时间内的“瞬时预测”。
预测模块所需要解决的问题,不仅仅局限于结合物理规律对物体做出预测,往往更重要的是结合物体和周边环境,以及积累的历史数据知识,对感知到的物体做出更为宏观的行为预测。例如在图2中,行为预测需要在宏观层面预测图中的车辆是否会保持直行还是右转通过路口。
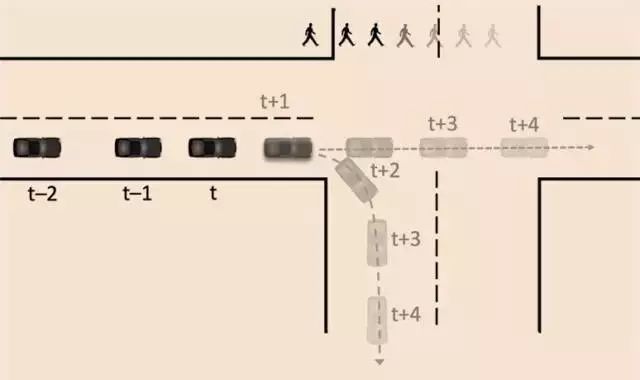
图2 无人车周边物体行为预测
行为预测的轨迹,既包括了障碍物在将来一段时间内运动的方向,还体现了它们在运动中的速度变化。譬如行人过马路的时候会预测他们使用较为恒定的步行速度,车辆转弯的时候会先减速后加速,而加减速的快慢也取决于弯道的弧度和长短。实际的无人车系统中,往往将宏观层面的行为预测和轨迹生成抽象成两个问题来解决。
宏观层面的行为预测问题,往往可以抽象成经典的机器学习问题,并且利用基于大数据的深度学习技术来解决。例如, 在假设车辆按照高精地图划分的道路(Lane)行驶的前提下,我们可以认为在任何一个时刻,车辆可行驶的每一个Lane序列都是一个需要进行Binary Classification(二元分类)的样本。
在这个假设下,我们不需要对直行、并道、路口拐弯等场景进行区分处理,因为无论是直行、并道,和路口拐弯,都可以统一看成是车辆在不同Lane序列上的行驶。车辆的宏观行为预测问题,便简化为对于Lane序列的Binary Classification问题。
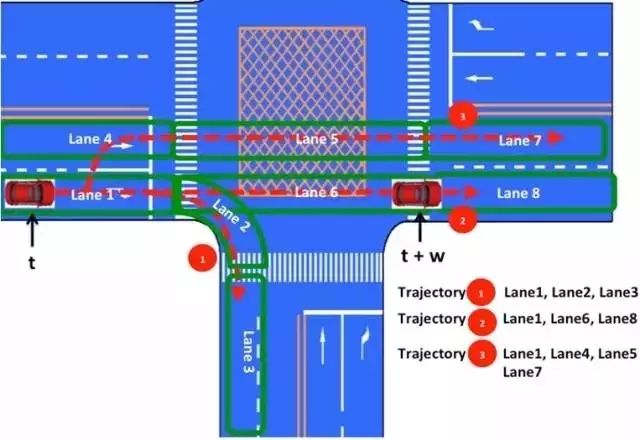
图3 无人车行为预测中的Lane序列Binary Classification抽象
如图3所示,在t时刻,无人车主车位于Lane 1,此时按照Lane序列的可能展开途径,我们考虑三条轨迹:
Trajectory 1: Lane 1、Lane 2、Lane 3对应路口右转;
Trajectory 2:Lane 1、Lane 6、Lane 8对应路口直行;
Trajectory 3:Lane 1、Lane 4、Lane 5、Lane 7对应换道后直行通过路口。
假设在t+w时刻,无人车经过Lane 6行驶到Lane 8的位置,那么轨迹Trajectory 2便成为该Binary Classification的正样本,其余两条轨迹便成为负样本。在这种基于Lane序列的问题抽象下,所有的正负样本可以从历史数据的回放中获得,并成为模型训练的样本数据。另一方面,模型的特征抽取可以结合一定时间内的如下信息来设计:
车辆本身的物理信息:速度、朝向等;
车辆相对于道路的信息:在Lane上的横向/纵向位移和速度,相对Lane边界的距离等;
车辆周边的其他物体的信息:车辆周围例如左右相邻Lane是否有障碍物等。
在上述的样本标签定义和特征抽取下,无人车Prediction部分的宏观行为预测可以很好的抽象成典型的机器学习问题来解决。在预测得出的宏观行为基础上,相关的轨迹生成和速度预测可以通过特定的规则或者物理模型来实现。
路由寻径(Routing)
无人车路径规划的Routing寻径问题,虽然也是要解决从A点到B点的路由问题,但由于其输出结果并不为实际的驾驶员所使用,而是给下游的行为决策(Decision)和动作规划(Planning)等模块作为输入,其路径规划的层次要更加深入到无人车所使用的高精地图的车道(Lane)级别。
如图4所示,其中的箭头线段代表高精地图级别的道路划分和方向。
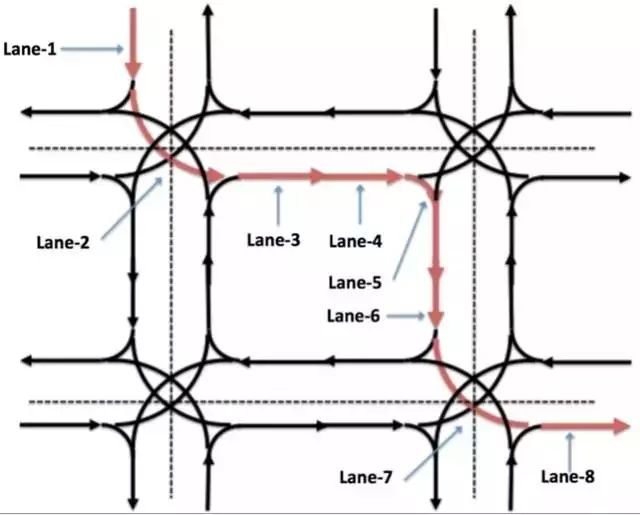
图4 无人车路由寻径模块(Routing)的高精地图道路(Lane)级别寻径路由
Lane1、Lane2………Lane8构成了一条Routing输出的路由片段序列。可以看到,无人车地图级别的Lane划分并非和实际的自然道路划分对应。比如Lane2、Lane5、Lane7都代表了由地图定义绘制的“虚拟”转向Lane。类似的,一条较长的自然道路,也可能被划分为若干个Lane(例如Lane3、Lane4)。
作为整体无人车决策控制规划(Decision,Planning&Control)系统的最上游模块,路由寻径模块的输出严格依赖于无人车高精地图(HD-Map)的绘制。在高精地图定义绘制的路网(Road Graph)的道路(Lane)划分的基础上,以及在一定的最优策略定义下,路由寻径模块需要解决的问题是计算出一个从起点到终点的最佳道路(Lane)行驶序列:{(lane,start_posotion,end_position)i},其中,(lane,start_posotion,end_position)i我们称作一个Routing Segment(路由片段),所在的道路由lane来标识,start_posotion,end_position分别代表在这条道路上的起始纵向距离和结束纵向距离。
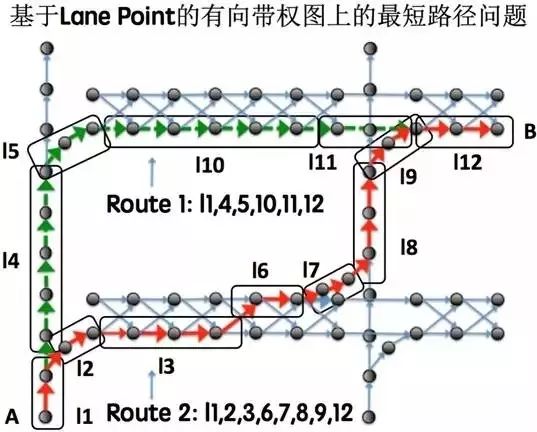
图5 无人车寻径(Routing)基于Lane Point的有向带权图上的最短路径问题抽象
我们可以把无人车在高精地图的Lane级别寻径问题,抽象成一个在有向带权图上的最短路径搜索问题(如图5所示)。
路由寻径(Routing)模块首先会基于Lane级别的高精度地图,在一定范围内所有可能经过的Lane上进行分散“撒点”,我们称这些点为“Lane Point”。这些点代表了对无人车可能经过的Lane上的位置的抽样。
这些点与点之间,由有向带权的边进行连接。Lane Point之间连接的权,代表了无人车从一个点行驶到另一个点的潜在代价(Cost)。在这样的有向带权图的问题抽象下,路由寻径问题可以利用常见的A*算法或者Dijkstra算法来进行实现。
行为决策(Behavioral Decision)
行为决策(Behavior Decision)层在整个无人车决策规划控制软件系统中扮演着“副驾驶”的角色。这个层面汇集了所有重要的车辆周边信息,不仅包括了无人车本身的当前位置、速度、朝向以及所处车道,还收集了无人车一定距离以内所有重要的感知相关的障碍物信息以及预测轨迹。行为决策层需要解决的问题,就是在知晓这些信息的基础上,决定无人车的行驶策略。这些信息具体包括:
-
所有的路由寻径结果:比如无人车为了达到目的地,需要进入的车道是什么(Target Lane)。
-
无人车的当前自身状态:车的位置速度朝向,以及当前主车所在的车道。
-
无人车的历史信息:在上一个行为决策(Behavioral Decision)周期,无人车所做出的决策是什么?是跟车,停车,转弯或者是换道?
-
无人车周边的障碍物信息:无人车周边一定距离范围内的所有障碍物信息。例如周边的车辆所在的车道,邻近的路口有哪些车辆,它们的速度位置如何?以及在一个较短的时间内它们的意图和预测的轨迹。周边是否有自行车或者行人,以及他们的位置速度轨迹等。
-
无人车周边的交通标识信息:一定范围内的Lane的变化情况。比如路由寻径的结果是在Lane1的纵向位移10m处换道进入对应的相邻Lane2的纵向位移20m处,那么Lane1的合法的纵向位移换道空间是多大?比如从一个直行Lane行驶结束,需要进入下一个左转Lane,两条Lane的交界处是否有红绿灯或者人行道?
-
当地的交通规则:例如道路限速,是否可以红灯右拐等等。
无人车的行为决策模块, 就是要在上述所有信息的基础上,做出如何行驶的决策。
可以看出,无人车的行为决策模块是一个信息汇聚的地方。由于需要考虑如此多种不同类型的信息以及受到非常本地化的交规限制,行为决策问题往往很难用一个单纯的数学模型来进解决。往往更适合行为决策模块的解决方法,是利用一些软件工程的先进观念来设计一些规则引擎系统。
例如在DARPA无人车竞赛中,Stanford的无人车系统“Junior”利用一系列cost设计和有限状态机(Finite State Machine)来设计无人车的轨迹和操控指令。在近来的无人车规划控制相关工作中,基于马尔可夫决策过程(Markov Decision Process)的模型也开始被越来越多得应用到无人车行为层面的决策算法实现当中。
简而言之,行为决策层面需要结合路由寻径的意图,周边物体和交通规则,输出宏观的行为层面决策指令供下游的动作规划模块去更具体地执行。其具体的指令集合设计则需要和下游的动作规划模块达成一致。
动作规划(Motion Planning)
在行为决策层下游的模块是动作规划(Motion Planning)。
其任务是具体将行为决策的宏观指令解释成一条带有时间信息的轨迹曲线,来给最底层的反馈控制来进行实际对车的操作。更具体而言,动作规划模块试图解决在一定的约束条件下优化某个范围内的时空路径问题。
这里的“时空路径”指车辆在一定时间段行驶的轨迹。该轨迹不仅包括位置信息,还包括了整条轨迹的时间信息和车辆姿态:即到达每个位置的时间,速度,以及相关的运动变量如加速度,曲率,曲率的高阶导数等。
动作规划可以拆分成为两个问题:轨迹规划(Trajectory Planning)和速度规划(Speed Planning)来解决。其中轨迹规划只解决在二维平面上,根据行为决策和综合地图信息定义的某种Cost函数下,优化轨迹的问题;而速度规划问题则是在选定了一个或者若干个轨迹(Trajectory)之后,解决用什么样的速度来行驶的问题。
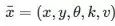
,其中(x,y)表示车辆在二维平面的位置,θ表示车辆的朝向,k表示曲率(也即朝向θ的变化率),v表示车辆的速度(即轨迹任意点的切线速度)。车辆的这些姿态变量的标量大小满足如下关系:
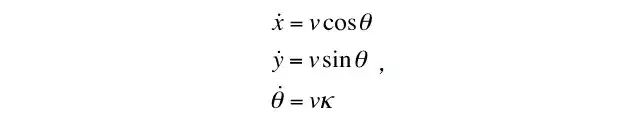
其中曲率的k大小往往由系统的输入限制条件决定。在此基础上,考虑一条由车辆运动产生的连续轨迹(Path)。我们称沿着轨迹的方向的位移为S方向。轨迹相对于车辆姿态的系统关系由下列偏微分方程式给出:

我们的轨迹规划(Trajectory Planning)算法非常依赖于地图对于道路的定义。这里我们定义道路由其道路中心线(Center Line)所定义,且定义道路的采样函数为:
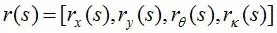
,其中s代表道路的中心线切向方向的位移(也称为纵向位移s)。与此对应的是道路的中心线垂直方向位移l,也称之为横向位移。如果考虑一个车辆的姿态点p点在道路上(s,l)坐标,那么其实际的姿态和(s,l)的关系
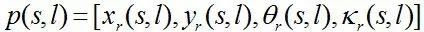
满足:
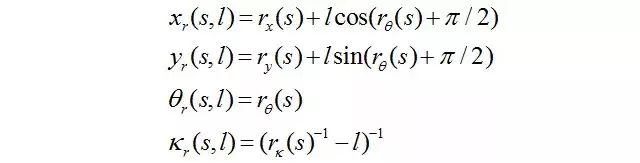
其中曲率Kr定义为在道路转弯的内侧曲率加大(随纵向位移l加大),外侧曲率则减小。我们使用右手坐标系,所以如图6所示在靠近原点处朝x轴的正方向,纵向位移l朝着y轴正方向加大。
假设对于某条道路Lane(k),其纵向宽度lk保持不变。那么该条道路变可以表示成为一个随着中心线横向位移s的点集{p(s,lk):s∈R+} 。我们称这样的一个坐标系统为坐标系统。
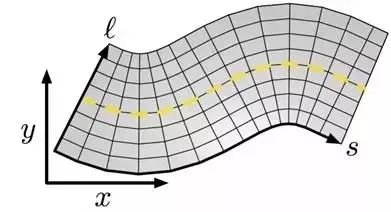
图6 XY平面下的SL坐标系统及其网格划分
在上述的车辆模型和道路模型下,我们讨论轨迹规划所产生的轨迹曲线。
首先我们定义车辆的轨迹(Trajectory)为一个从[0,1]区间到车辆姿态向量集合C={x⃗ }的连续映射:ρ:[0,1]→C 。其中,车辆的初始姿态向量为x⃗ =(x,y,θ,k)。每条轨迹终点处如图7所示,轨迹1的终点姿态为ρ1(1)=qend1轨迹2的终点姿态向量为ρ2(1)=qend2 ,初始姿态为ρ1(0)=ρ2(0)=qinit。
轨迹优化的目标便是在所有可能的轨迹曲线中,筛选出满足边界条件的轨迹曲线,再寻找一条/若干条平滑且Cost函数最低的曲线。其中轨迹的候选曲线我们用类似在路由寻径(Routing)模块中介绍的“撒点”的采样方式来生成。
参考图7,在某条Lane的SL坐标系下,我们按照均匀切分的S和L方向的方格内,在固定S和L间隔下,考虑每个(si,lj)区域的中心点(如图7所示,又称为轨迹点Trajectory Point)。
一条候选的轨迹(Trajectory)便可以看做是沿着Lane的中心线纵向位移s方向连接不同Trajectory Point的平滑曲线。在图7所示的道路SL分割和采样下,可能的Trajectory Point有16个(4个s位置,4个l位置),从车辆的初始位置出发,我们只考虑在s方向单调增大的可能,不考虑城市综合道路行驶中的倒车情况,那么总的候选曲线的总条数为44=256条。轨迹优化便是要在这256条候选的曲线中找出Cost最优的轨迹。
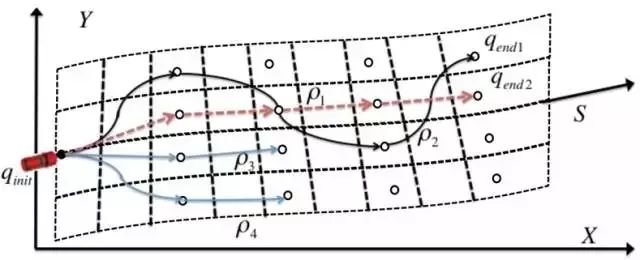
图7 SL坐标系下道路的分割采样以及可能的轨迹
我们采用多项式螺旋线来连接轨迹点Trajectory Point,从而生成候选的曲线。多项式螺旋线,如图8所示,代表了一类曲率可以用弧长(对应我们轨迹中的s方向)的多项式函数来表示的曲线簇。我们使用三阶(Cubic)或者五阶(Quintic)的多项式螺旋线,其曲率K和轨迹弧长S的关系K(S)为:
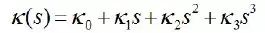
或者
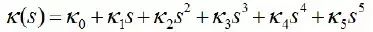
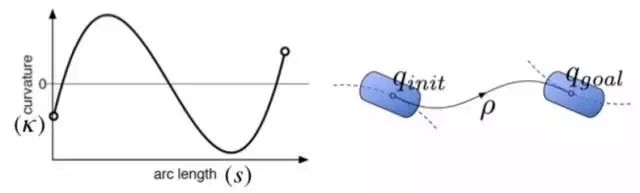
图8 多项式螺旋线以及车辆姿态的螺旋线示意图
基于这种使用三阶(五阶)螺旋线连接的轨迹(Trajectory),其参数可以快速有效的通过梯度下降(Gradient Descent)的方法来搜索。以三阶多项式为例,我们考虑从车辆初始姿态qinit=(xI,yI,θI,KI)到目标姿态qgoal=(xG,yG,θG,KG),且具有连续曲率的三阶螺旋线:
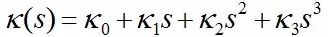
在初始状态 时,考虑曲率的一阶导数和二阶导数均需要满足初始状态的限制,我们可以得到:
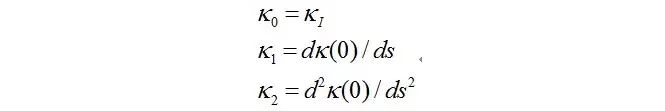
这样使得实际未知参数减少到2个(K3,SG),利用梯度向量我们可以快速寻找到非常接近初始状态限制的三阶螺旋线的参数。在上述的所有候选曲线中,我们可以根据业务的不同需要来设置Cost函数,然后选择出在任何时间点Cost最小且满足边界条件限制的曲线。
由于候选曲线随着我们采样间隔随指数增长,往往将Trajectory Point建立成某种有向带权图,然后利用图论中的搜索方法结合Cost设置来选取最优曲线。具体的搜索方法可以参考中的动态编程方法。
在轨迹规划选定了一条或者若干条曲线后,速度规划部分将决定车辆以什么样的速度来通过这条曲线。轨迹规划在选取曲线时的Cost设置偏重于静态障碍物,而速度规划在选取曲线时的Cost设置应该注意以下几点:





