
稿件转载自公众号:城市数据团 ID:
最近在知乎上看到一个很有趣的问题:房间里有100个人,每人都有100元钱,他们在玩一个游戏。每轮游戏中,每个人都要拿出一元钱随机给另一个人,最后这100个人的财富分布是怎样的?
以下是三个不同的答案,请投票:
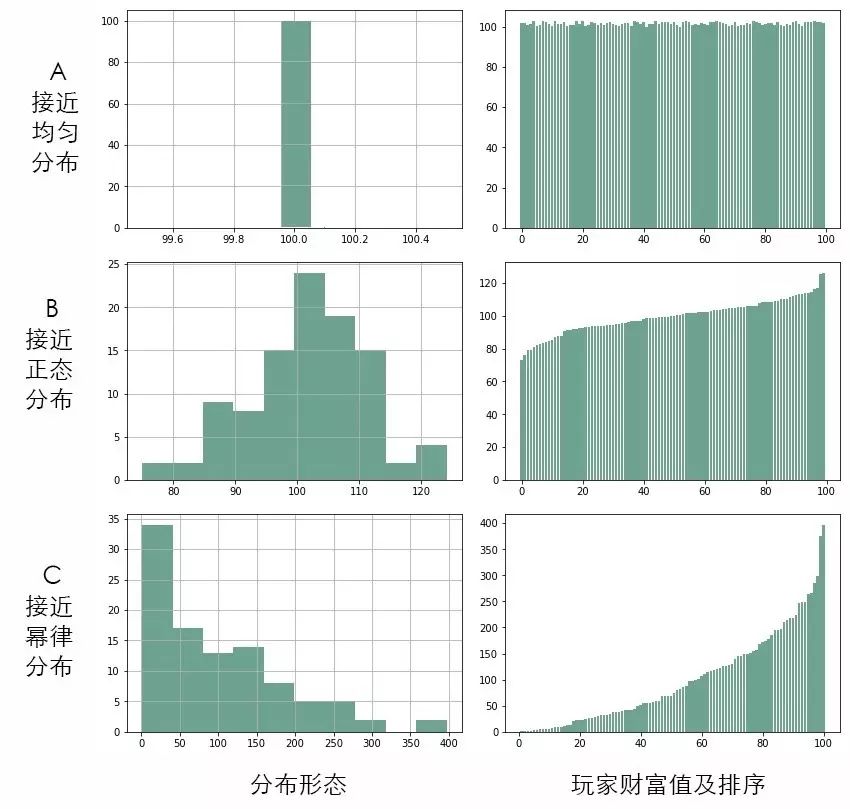
我们不妨把这场游戏视作社会财富分配的简化模型,从而模拟这个世界的运行规律。
我们假设:每个人在18岁带着100元的初始资金开始玩游戏,每天玩一次,一直玩到65岁退休。“每天拿出一元钱”可理解为基本的日常消费,“获得财富的概率随机”是为了……嗯……简化模型。以此计算,人一生要玩17000次游戏,即获得17000次财富分配的机会。
下面我们来回答一下。
在上述规则下,游戏运行17000次的结果如下图所示:
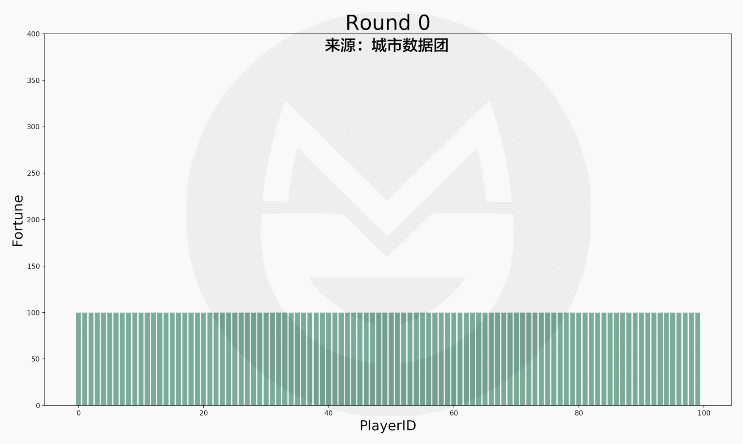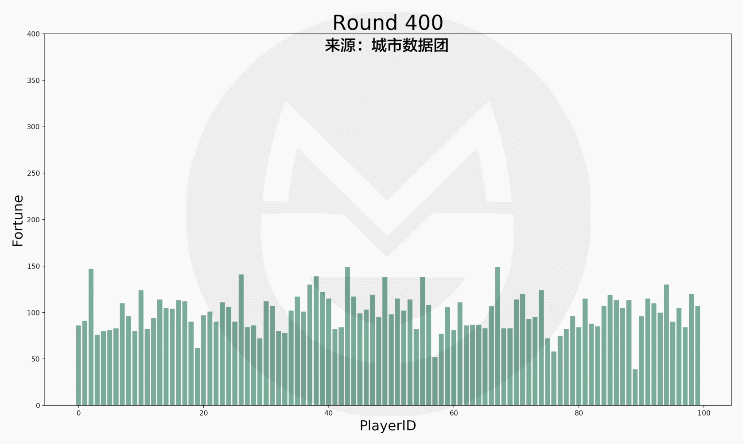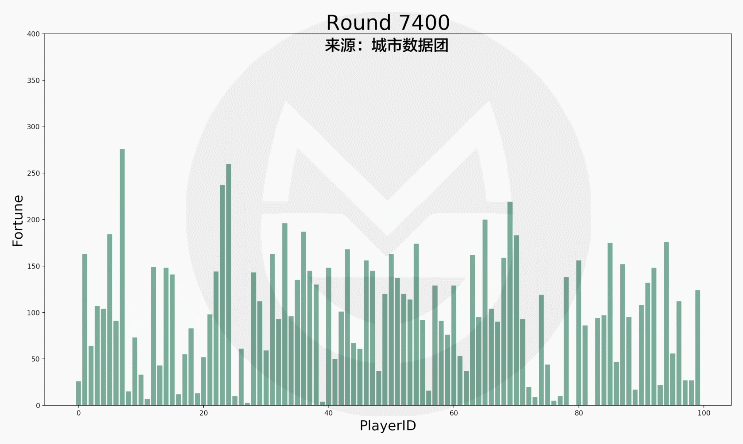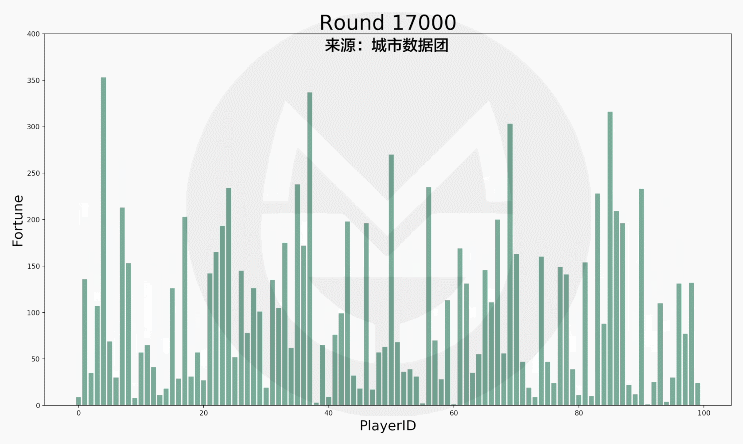
(说明:1.上图中横轴标签代表一个玩家的编号,柱子的高低变动反映该玩家财富值的变化。2. 当某人的财富值降到0元时,他在该轮无需拿出1元钱给别人,但仍然有机会得到别人给出的钱。)
可以看到,每个玩家财富值的变动是极为剧烈的。为了方便描述整个社会财富的分配状况,我们又按照财富值的排序做了下图:
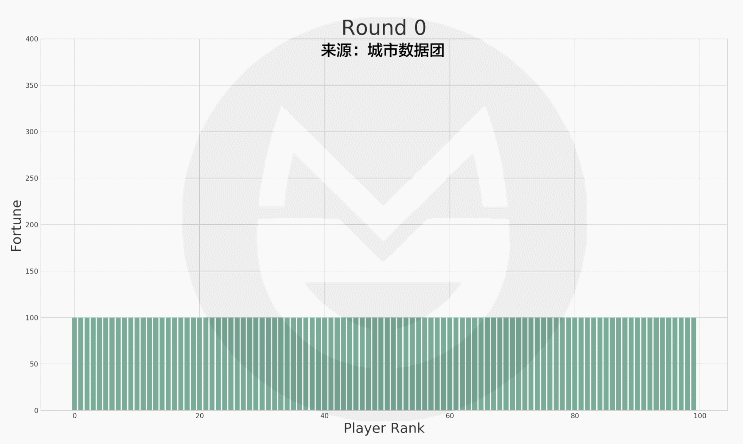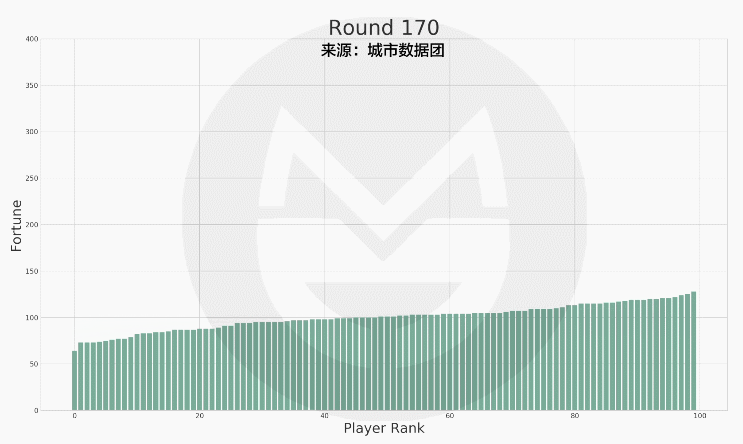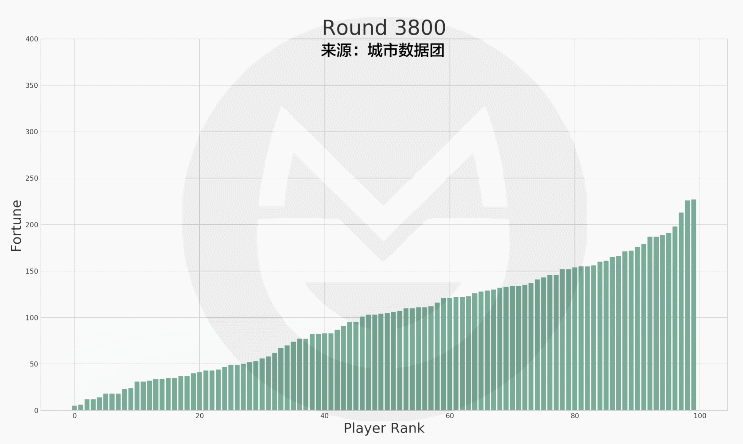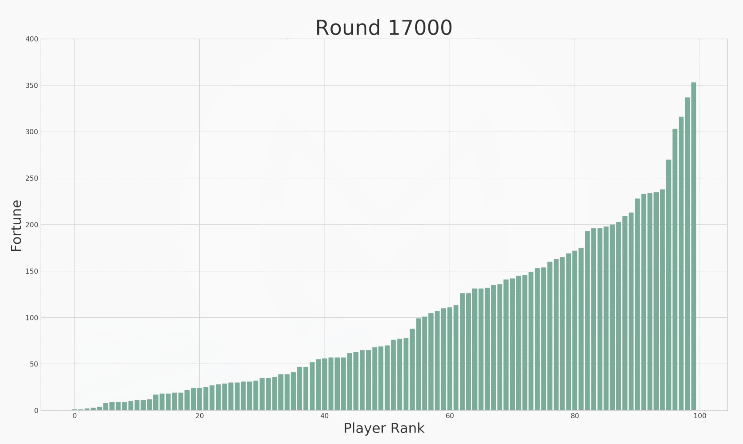
(说明:上图中横轴标签代表玩家排序(非编号),排序越高的财富越多。初始时所有人的财富值相等,随着游戏的进行,财富值差距越来越大。)
没错,财富的分配接近于幂律分布(结论只是程序模拟,而非数学精确求解)。最后,社会将有很少的富人和很多的穷人:
就这样,大部分人的钱跑进了少部分人的口袋里。即使在最公平的规则下,世界依然展现出了残酷的一面。
在此基础上,我们又设计了更多的情景,同样用程序进行了模拟。
在现实社会中,情境会更复杂一些。比如说,当我们没钱了,还可以找亲友、找银行、找投资人借债,说不定哪天就东山再起了呢。在允许借债的情况下,游戏结果如下图所示(排序后结果):
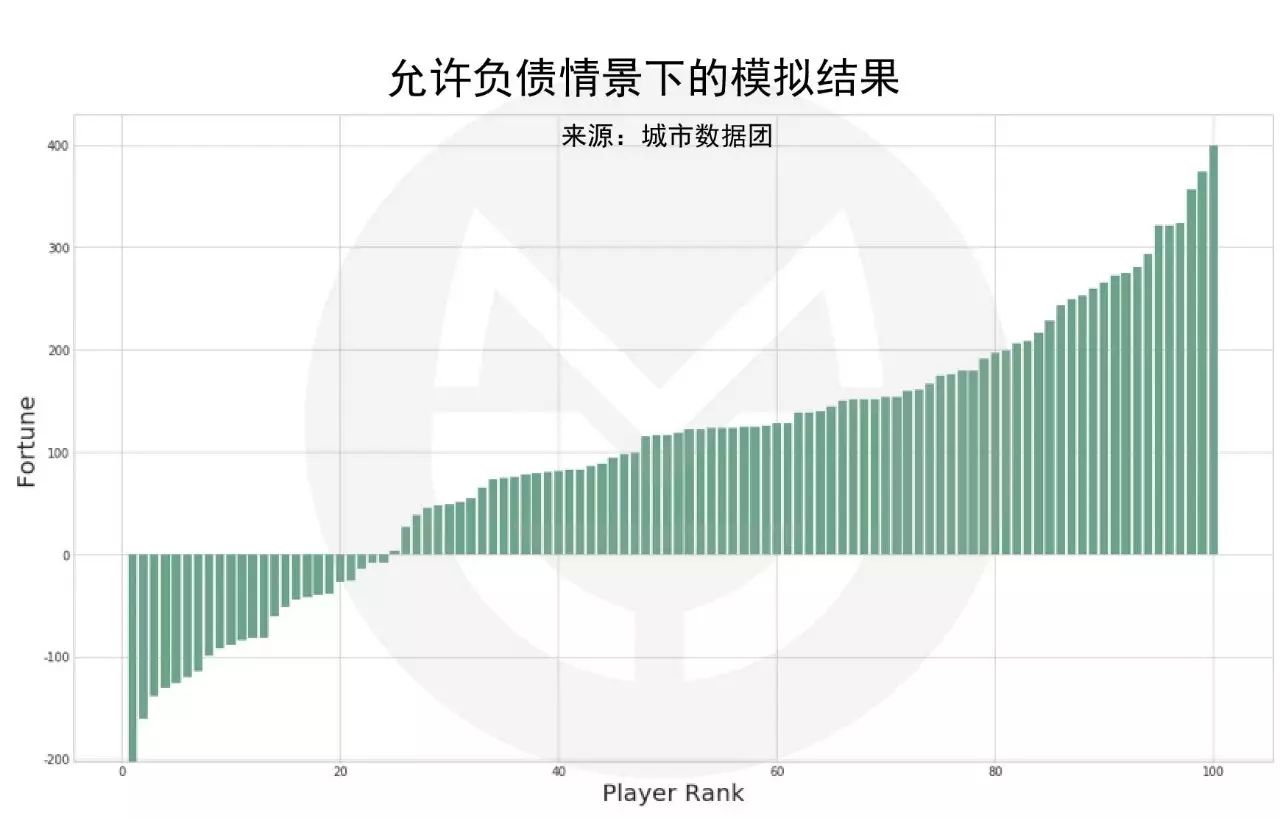
结果表明:
没错。借债虽然能让我们在走投无路时多一些周转余地,但最终会让穷人变得更穷。
我们以所有玩家财富值的标准差来衡量社会贫富分化程度,按时间序列做出图来长这样:
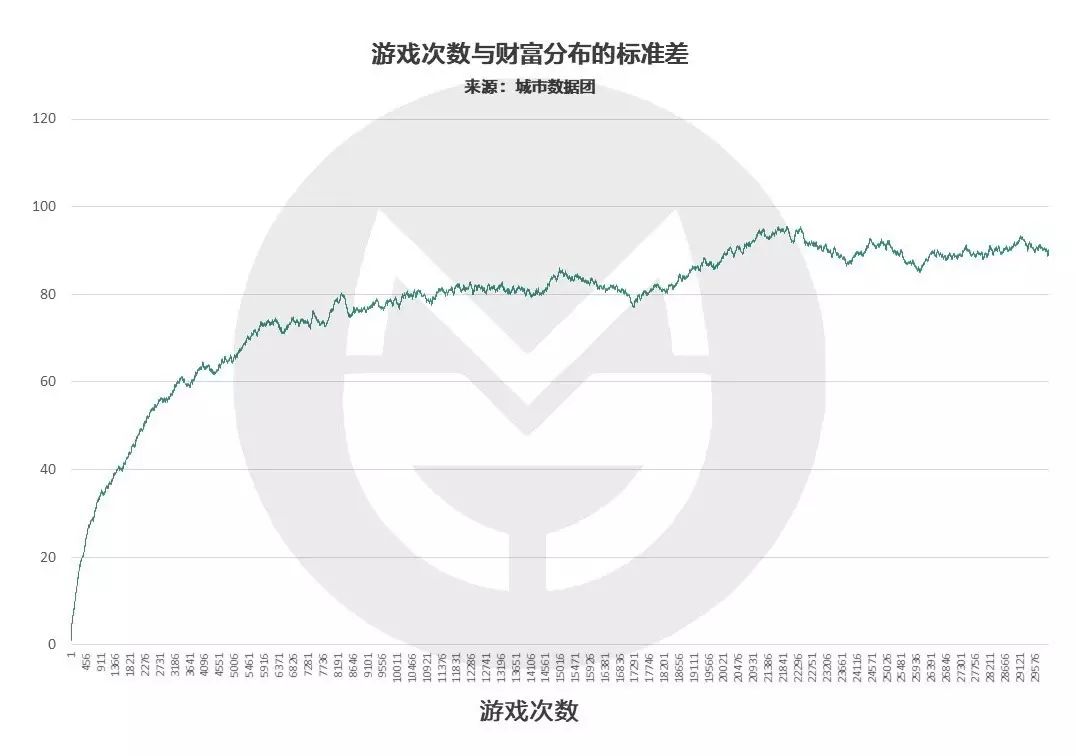
(说明:横轴表示游戏轮数,纵轴表示社会财富的标准差)
可以看到,游戏早期的标准差变动最为激烈,而在6000-6500轮游戏后,标准差的变化趋于平缓,也就是社会财富分布的总体形态趋于稳定了。按照我们设定的游戏与人生的对应规则,这时玩家年龄为35岁。
这个结果告诉我们,35岁之前,人与人之间的差距已经完全拉开了。
进一步看,如果一个人在35岁时破产,还有没有可能逆袭呢?
本次模拟结果中,有15个人在35岁的最后一天时处于破产(负债)状态,而他们在此后的财富值及排名如下图所示:
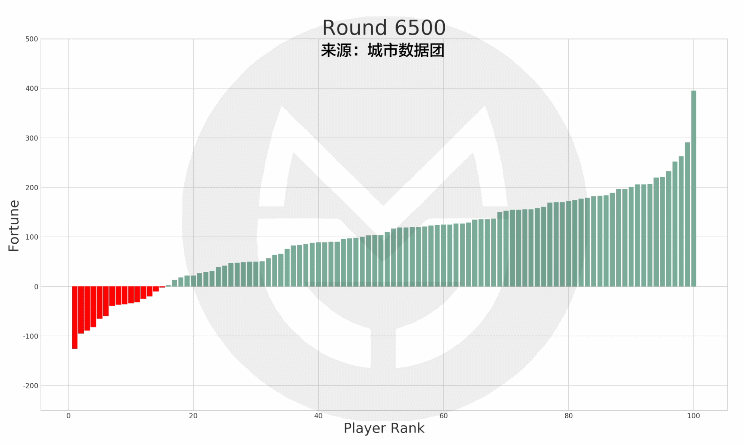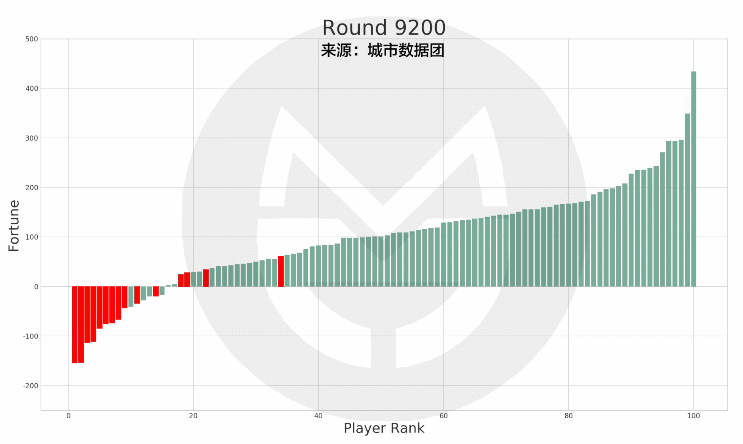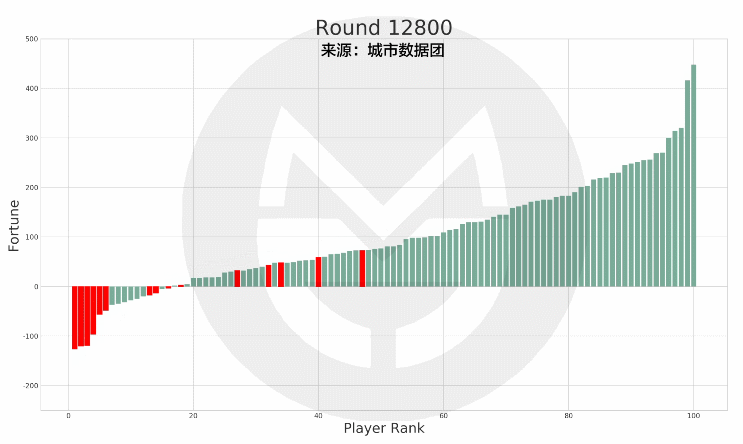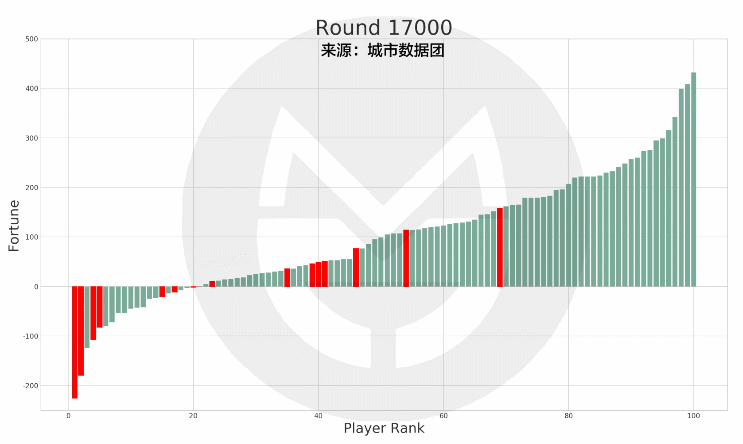
(说明:上图中的红色柱子为在35岁时破产的玩家,绿色柱子为其他玩家。红色柱子在纵轴上的高度变化表示其财富值变化,在横轴上的位置变化表示其排名变化。)
可以看到,当这15个人在65岁退休时,有7人仍然处于破产状态;有8人还清债务并有了财富积累,但离富豪仍有相当差距。
看来,以35岁为界,虽然破产以后,仍有一半概率回复到普通人的生活,但想要逆袭暴富,却是相当困难的。
所以,发财要趁早,大龄屌丝逆袭更像是一个传说。
在真实社会中,每个人的起点其实并不相同。总有一些富二代、富三代,在财富游戏的开始就占尽了便宜。这一点也应该被考虑到我们的模型中。
为了简化计算,我们假设只有两类玩家:90个普通玩家(设定同上)+10个富二代玩家。富二代玩家的初始财富是500元,他们在每轮游戏中需要拿出2倍的钱,同时获得财富的几率也是普通人的2倍。游戏结果如下图所示(排序后结果):
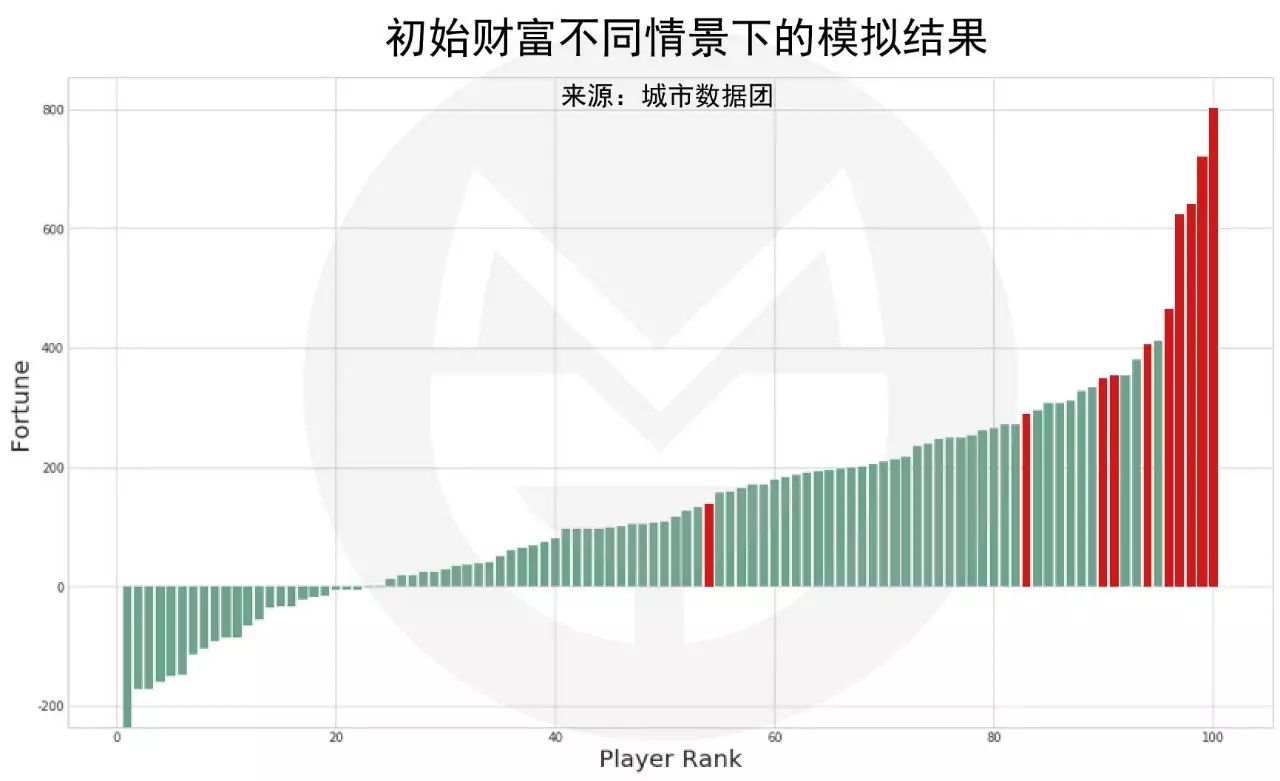
(说明:上图中的红色柱子为富二代玩家,绿色柱子为普通玩家。)
虽然这个分布形态与全是普通玩家的结果基本一致:
top10和top20的富人掌握的社会财富比例和负债的人数比例都差不多,但是仔细来看,top5富人中的全部,以及top10富人中的7位都是富二代玩家。
我们在富二代玩家(红色线条)和普通玩家(绿色线条)中各选5位,绘制出他们的财富值变化图:

可以看到,富二代玩家中虽然也有“败家子”,但他们仍有很大概率将财富值维持在较高水平。富二代们和普通人生活在两个世界中,偶有交集而已。
没错,普通人要有极好的运气,才能到达与败家富二代相同的高度。
为了缓和贫富分化带来的诸多矛盾,在真实社会中有许多转移支付的手段,税收就是其中一种。
本轮游戏中,玩家的初始财富同为100元,每轮游戏中玩家获得1元钱的概率相等。但若被选中的玩家在该轮游戏时的财富值高于200元,则他只能获得60%的收益;而另外40%的收益将平分给财富值低于0元的所有玩家(相当于破产者的低保)。模拟结果如下图所示:
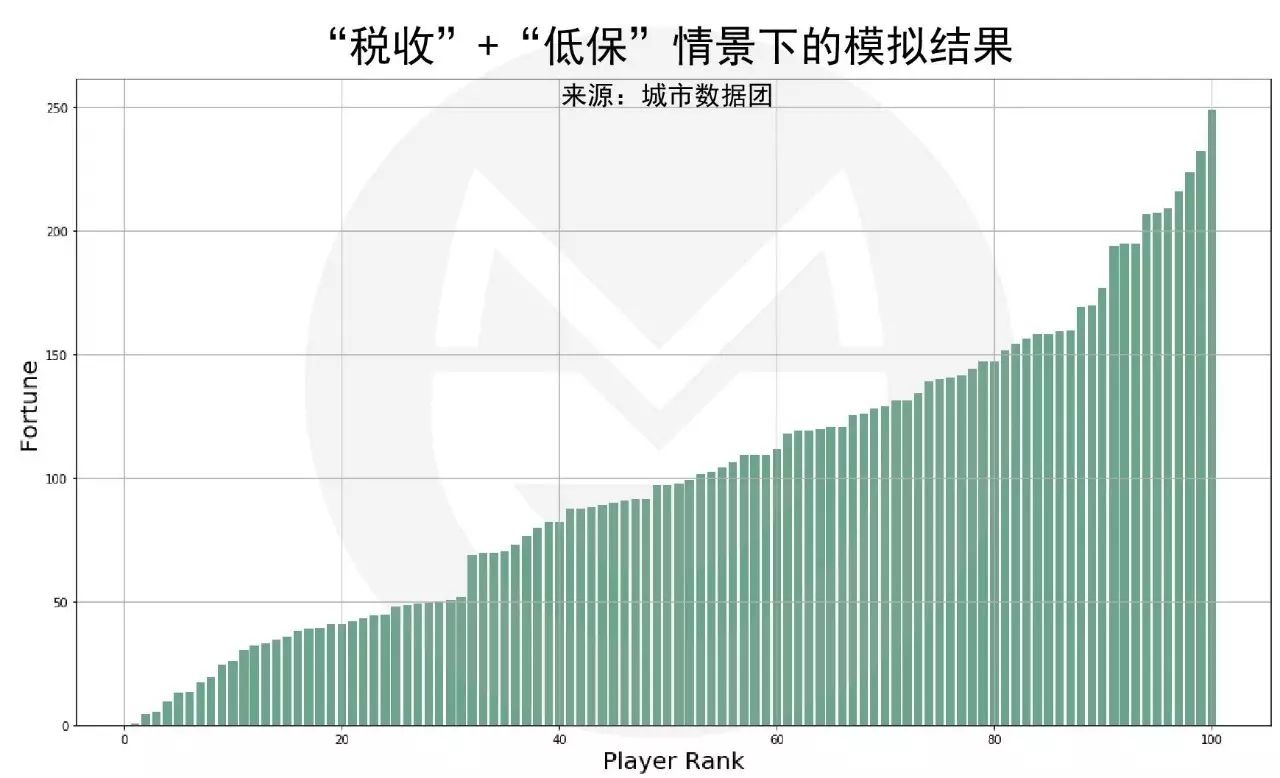
可以看到,在“税收+低保”的游戏规则下,社会财富分布仍然是高度极化的,区别只是基本消灭了破产者,同时富有的人没那么富了而已。
收税可以平缓世界的分化,但是并不容易改变世界的残酷本质(除非大大加强转移支付的力度)。
我们中的绝大多数人,没有一飞冲天的发财运气,也没有腰缠万贯的爹,更不甘于吃低保。想要改变命运,我们只能选择自己更努力,去争取更好的生活。
我们假设每个玩家的初始财富仍然为100元,但有10人比别人加倍努力,从而获得了1%的竞争优势,即赢得收益的概率比别人高出1%,模拟结果如何呢?
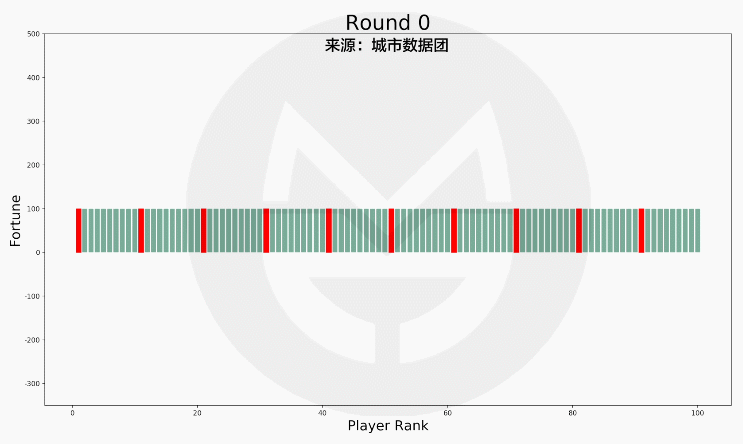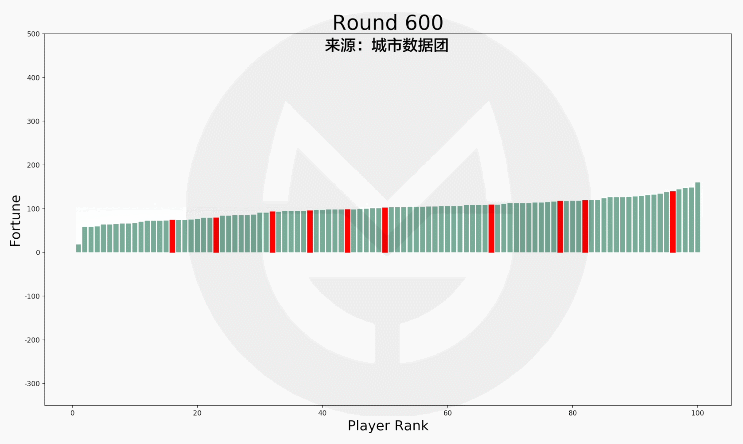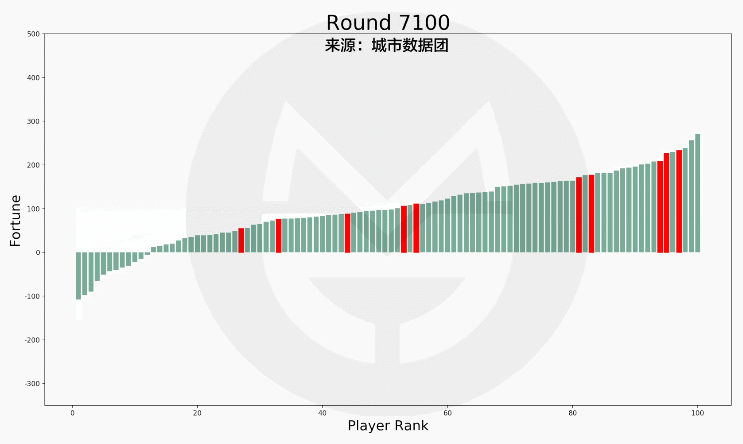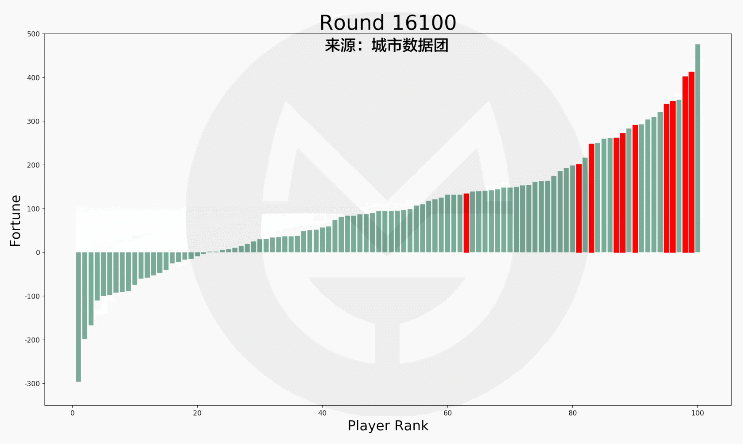
(说明:上图中的红色柱子为更努力的玩家,绿色柱子为普通玩家。)
可以看到,社会财富的总体分布形态没有什么变化。但是,10位努力玩家中的9位都进入了富人top20!
是的,尽管最成功的玩家不一定是最努力的那个,但是努力的人大都混的还不错。感谢这个残酷世界还给我们留下一条生路。
看到这里,相信各位读者已经对这个问题有了自己的答案:
那就是
努力
并坚持下去!
















