“人在江湖漂，不能白挨刀”——用数学揭秘猜姓氏把戏

作者：林开亮，转载自“数学纵贯线”

作者注：本文原是连载于“好玩的数学”的两篇文章，现为方便读者合二为一。

我第一次去城里，是在很小的时候——20多年了，也许是小学五六年级，跟着一个种菜的表姑妈推着板车去常德县城蔬菜市场卖菜。我当时一定头一次吃到不少好吃的，但现在想不起来了，不过我还记得当时我拆了一个算命先生的台，为此我表姑妈颇为得意。这种猜姓氏的把戏估计大家都见过，以下是我当时遇到的版本。

首先算命先生会摊开一张百家姓的大图纸，里头有很多小格子，每个小格子里有一定数目的姓氏，大图纸旁边会放一些小纸片，每张小纸片上会有一定数目的姓氏。他会要求你用有你姓氏的小纸片盖住大图纸上那个有你姓氏的格子，然后他“掐指一算”，就报出了你的姓氏。我见识过几次，没有不准的，来算命的无不称奇慨叹！我也好奇他是怎么做到的，后来我想明白了，一定是 小纸片和盖住的小格子上只有一个相同的姓氏 。我拿起小纸片一对照，果不其然。后来，我也开始卖弄了，只要有人用小纸片盖好小格子，我就拿起来迅速一对照，结果有几次比算命先生还先得出结果，我记得当时猜中一人姓蒋（与委员长同姓，所以印象深刻）。他老人家脸上开始不好看了，于是就喝令我一边玩去。

20多年过去，大街上仍然有算命先生玩这个把戏，仍有不少人疑惑不解，乃至迷信其神。网上有不少朋友追问这个把戏究竟什么玄机，也有人解密，不过他们似乎没有真正讲明白这一点—— 如何保证 小纸片和盖住的小格子上只有一个相同的姓氏 ？例如，见2017年春节期间的一个视频。

这里我想介绍一个思路（最近偶然想到，算命先生也许用别的，但我想绝不至于比这方法还简单了），它也许是最简单的，可以保证每个人都能当一回“神算子”。

首先 ，我们要有一张 大图纸 ，上面分布着常见的百家姓。按照百度百科，

《百家姓》，是一篇关于中文姓氏的文章。按文献记载，成文于北宋初。原收集 姓氏 411个，后增补到568个。

为简单起见，我们这里仅选取出现频率最高的前 300 个姓氏，以下排名取自网络（排序是否准确与猜姓氏无关，要紧的是，我们只需要给出一个排序）。

2017年中国人口最多的前300大姓

2017年中国人口最多的前100至200大姓

2017年中国人口最多的前200至300大姓

你现在设想，这300个姓氏被摊在一张具有 12个小格子的 纸上，每个格子有 25 个姓，第 i 个格子对应的那25个性，其序号恰好对应于那些被12除余i的数，即形如12k+ i （其中k=0,1,2，…24 ）的数，例如，

第 1 个格子所对应的姓，是以下25个（序号形如12k+ 1 ，k=0,1,2，…24），我们排成5行5列【此处要感谢 启功 先生 】：

第 2 个格子所对应的姓，是以下25个（序号形如12k+ 2 ，k=0,1,2，…24）：

类似地，可列出第3个、第4个……第12个格子所对应的25个姓氏，由于剧情需要， 我们这里再给出 第 4 个格子所对应的25个姓（其序号形如12k+ 4 ，k=0,1,2，…24）：

总共恰好有300个姓氏。注意，为了方便起见，更可取的是，会在每个格子里标注一个数字，表明其中各个姓氏所对应的序号被12除的余数。例如，上图很可能标记为

接下来到了第二步，构造25张小卡片，每张纸上有12个姓氏。 现在也许你都可以猜到怎么构造了。

第 j 张小卡片上的姓氏所对应的序号为 25l + j , 其中 l=0, 1, 2, …，11。

例如，第 1 张小纸片上的12个姓氏（对应序号为25l+ 1 ，其中l=0,1,2,…，11）为

第 2 张卡上的12个姓氏（对应序号为25l+ 2 ，其中l=0,1,2,…，11）为

…………………………………………………………………………………………

类似地，可以造出全部25张卡片。为剧情需要，我们再列出第 16 张卡片上的12个姓氏（对应序号为25l+ 16 ，其中l=0,1,2,…，11）为

现在我们可以保证，第 j 张卡片与第 i 个格子恰好只有一个相同的姓。 这里隐含了一个著名的数学定理，数论中有名的 中国剩余定理。 在我们的情况，它相当于说：

设 i ， j 是给定的整数，则在1到300这些数中，有且仅有一个整数 x 同时满足下述两个条件：x被12除余 i ，x被25除余 j 。并且这个x可以这样求得，令 y=25i-24j , 则 x=y+300k，其中k是一个适当的整数， 使得x在1到300之间。

注意，要紧的是，12 与25 互素 （即能够同时整除它们的正整数只有1），且300恰好是它们的乘积。

回到我们原来的问题，不难从上述表达式分析得到下述结果：

若 i ≥ j ，则 x 恰好是第 j 张卡片上的第s个姓氏；这里s=（ i - j +1）+12 t，其中t是一个适当的整数， 使得s在1到12之间。

注意，根据这个分析， 我们不需要知道（或记忆）那300个姓氏的序号，只需要知道，i与j，并且从第 j 张卡片就可以读出 x，它就在第(i-j+1)个位置——在模12的意义下。只要你会做两位数以内的加减法，会数数，你就会玩这个把戏了！

好了，道具已经备齐，现在我们可以玩把戏了。

比如在本人的情况，当我告诉了你，我的基本信息是i=4, j=16以后，你立即可以算出

i-j+1=4-16+1=﹣11，

从而s=1（取t=1），也就是说，我的姓在第16张卡片（见上图）的第一个位置，即我跟 紫霞 同姓（紫霞当然姓林了，因为她的姐姐青霞的全名是 林青霞 ）：

好了，我想很多人应该会有兴趣尝试一下了，来吧，实践出真知。只有当你完全准备好以上 12 + 25 =37个道具以后，你才能对姓氏在这300个姓氏中的朋友玩转这个游戏。（无论如何，虽然这营生成本低，我还是希望各位读者不要学了这把戏去挣钱。你想想，要是做个简单的减法都能挣钱，那是不是也来得太容易了！请大家尽量转发分享这篇文章，提醒世人不要被算命先生故作玄虚的雕虫小技蒙蔽了！）

按照上述原理，你也可以自行设计不同规格的道具（ 也许一个更好的选择是600个姓氏，它分解为两个互素的数24与25的乘积 ），只要它们满足中国剩余定理的互素条件即可。对于需要了解 中国剩余定理 的朋友，我们将在关于初等数论的系列讲座中详谈。若要一睹为快，可以参看这里的一个PPT， 从射雕到九章——在天大理学院物理系的通俗报告 。当你清楚中国剩余定理的本质以后，应该不难理解我这里简单陈述而未加证明的结论。我们留给有兴趣的朋友吧！

小把戏背后其实藏着美妙的数学，对数学爱好者而言，这何尝不是一种惊喜？

思考 ：街头算命先生往往能够根据你的生肖猜出你的年龄，知道这是为什么吗？

比如说，如果我告诉你我属猪，而且你又能看出，我不足四十一朵花，又超过三十一枝芽，你猜我多大？

为方便你对照答案，可以告诉你，鄙人与下一版《射雕英雄传》同岁：

昨日我在本号发表的文章 算命是胡扯，猜姓却不然 引发了不少读者和朋友的反响，他们的反馈让我对这个小把戏有了进一步认识，因此今天我想趁热打铁，继续跟大家分享我的心得。

昨晚七点多钟发布完公众微信号，我最先接到本科同学刘新亮的电话，他现在天津耀华中学教数学。他跟我讲，看到这篇推送很高兴，因为他下周要去到上小学的孩子班上给讲点数学，他正发愁讲点什么内容好。看到这个，他眼前一亮，所以立即给我打了一个电话。我也觉得这个题目不错，至少准备道具很简单。一个班最多五六十人（准确地说，需要考虑的只是姓氏的个数，鉴于经常有同姓的同学，所以姓氏个数会更少），他准备十来张卡片就够了（比如说，56=7*8,7+8=15）。这个游戏尤其适合新生开学的第一堂数学课，当学生与老师都还不熟悉的时候，老师如果通过这个简单的游戏一下子就猜出学生姓什么，其形象一下子就高大起来了，同时学生们也立即记住了这个学生的姓氏，再进一步让学生说出自己的全名，这个印象就深刻多了！想到这些，我当时的得意之情，完全可以用下述图片来形容：

十点多快要入睡时，又收到了好友刘云朋的一条消息（今天上午也有网友在评论区留言表达了相同的意思，非常感谢！），我瞬间切换到下图：

云朋兄发给我的消息如下：

第一次知道这样的把戏，很有趣。我有一个表面上稍不同的理解：假设有100个姓，把它们排成10×10的方阵，然后将同一行的姓填入大图纸中的同一格，把同一列填入同一小图纸，于是每种大小图纸的组合就给出这个矩阵的行指标和列指标，从而标记了既处于指定行又处于指定列的那个元素。

他说的方法更简单了，我们就照他说的方法，来玩一个猜百家姓的把戏。首先，我们选取100个姓氏，如昨天一样，我们不妨从网络选取下表

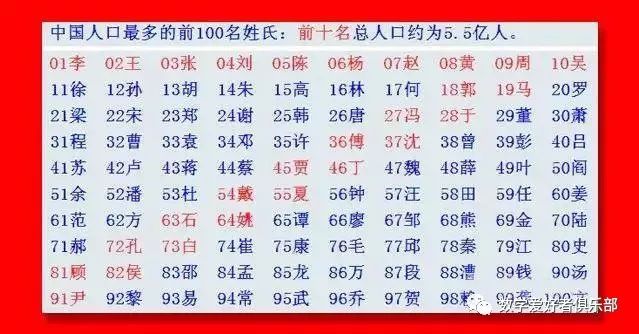
现在每一行的10个姓氏放入一个小格子，为让蒙蔽效果更好，我们可以将这10个姓氏排成三角垛，例如，第1行的10个姓氏（按照自然顺序）排成下述形状

第2行的10个姓氏（按照自然顺序）排成下述形状

依次类推，一直排到第10行。接下来再将每一列的10个姓氏排在小卡片上，如第1列的10个姓氏为

第2列的10个姓氏为

为剧情需要，我们再给出第6列的10个姓氏

好了，道具20张纸备齐以后，我们就可以来玩猜姓把戏了。比如，你可以确认一下，紫霞的姓（ 林 ，表格中对应坐标16）是不是满足这样的规律，它恰好在第6列的第2个位置。再如，你也可以验证金庸《倚天屠龙记》里那位风一样的女子的姓（ 杨 ，表格中对应坐标06）是不是也满足这样的规律。

容易发现，与上一篇介绍的用中国剩余定理的方法相比，刘云朋老师（任教于天津大学理学院物理系）介绍的上述方法更简洁，我反思了一下，发现我们的差别可以这样理解：

我之前思路是一维的（用数为坐标），而云朋兄这里的思路是二维的（用二个数为坐标）。他进化得比我多些。另一方面，原先的思路由于其复杂性，可能更不容易被外行发现。街头的各路神仙也许倾向于采取云朋这里的方法。

如果学生与老师都熟悉了，当然就不必猜学生的姓名了，这时候可以改为猜学生母亲的姓氏（只考虑那些随父亲姓的同学）。