欢迎点击「科学网」↑关注我们!
1917年,日本数学家挂谷宗一(かけやそういちSoichi Kakeya)提出了数学界著名的挂谷问题,其数学表述为:长度为1的线段在平面上做刚体移动,方式不限,转动也罢,平移也行,总之不惜采用任何手段,只求转过180度调头,试问:扫过的最小面积是多少?
他在提出此问题的同时,也给出了自己的猜测,也即至今未解的Kakeya猜想:最小单连通域的面积可能趋于零!
挂谷先生为何会提出这么一个烧脑的问题呢?原来他的祖国日本,人多地少,资源捉襟见肘,尤其体现在二战时闪转腾挪很憋屈,也难怪那时候提出了大东亚共荣圈的构想,不过在亚洲邻国眼里,这个共荣圈的本质就是侵略,远比不上中国如今的一带一路。
言归正传看一看问题的原型:一位武士在上厕所时遭到敌人袭击,矢石如雨,而他只有一根短棒,为了挡住射击,需要将短棒旋转一周360°(支点可以变化)。但厕所很小,应当使短棒扫过的面积尽可能小。面积可以小到多少?
如梭光阴已是2017年,算是该猜想等待证实或证伪的100周年大“庆”,尽管尚无成果可庆。
简略回顾求解历程:
正如1+1=2的哥德巴赫猜想一样,看似简单的数学证明,一定能吸引从文盲到大数学家的蜂拥而至。哎,想当年我也蠢蠢欲试。
为方便比较,所有给出值都规整为转过360度,除以2便可得扫过180度时的值。
先看没有技术含量的“文盲解”和“小学生的解”,前者以线段的任一端作为圆心旋转,后者以线段中心为圆点旋转,后者以节省75%的回旋面积完胜前者,简单得再添一句描述都显得多余。如下图所示:
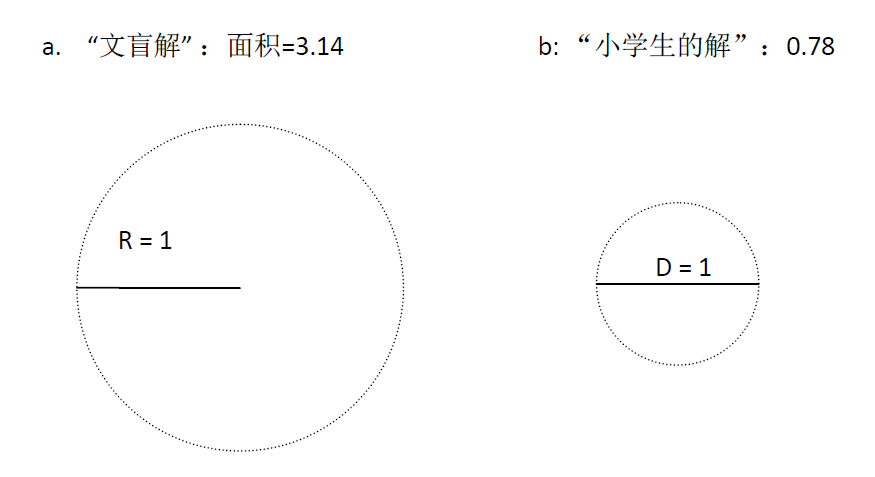
数学家们肯定不会考虑上述这些几乎没有技术含量的东西。在挂谷宗一提出这个问题后,有数学家发现,若这个线段在正三角形(高为1,边长为2/√3)中每一顶点处都旋转60°,可以算出这种情况下,线段扫过面积为1/√3= 0.58,比小学生的解0.78略有进步。如下图:
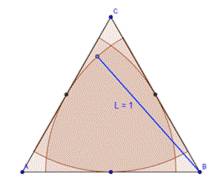
当然,若线段夹在两个圆之间,转过180°的面积既小于整个圆环,又大于半个圆环,当内圆的半径无限增大时,面积趋近于π/8,但始终不等于π/8= 0.39,比前者0.78又厉害了一倍多。如下图:
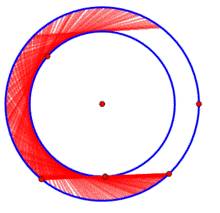
能否让扫过的面积刚好为π/8呢,挂谷宗一本人想到的是借助三尖内摆线,计算表明,这种情况下线段扫过的面积是π/8。挂谷本人及其他许多数学家都认为这就是最小面积了。
1928年,前苏联数学家贝西科维奇(Besicovitch,AbramSamoilovitch,1891-1970)差那么一点就解决了这个问题,答案是可以任意小。
精确描述并理解他的求解过程,得具有数学家的大脑,这显然也超出了本文的科普定位。有兴趣的朋友只好自行探究了。这里仅给出其中涉及到的佩龙树,如下图:
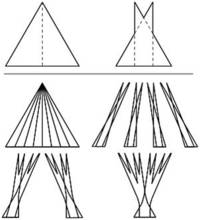
显然上述解答几乎50%地证明了挂谷猜想,唯一没能实现的是单连通域!也就是说调头过程中,线条难免有时要举高无限小高度再转一下,从一个连通域切换到另一个连通域。显然其意义大打折扣。
1971年坎宁安F.Cunningham终于在单位圆内作出面积可以非常小的单连通挂谷集,解决了单连通性和有界性两方面的问题。同时,他证明了如果限于星形(即图形内存在一点,连接它与图形中任一点的线段整个在图形中),则挂谷集的面积不小于π/108 = 0.029。
然而无限趋于零的单连通回旋面积仍然遥遥无期。
与此同时,地球上智商最高,甩了著名物理学家霍金一条街,IQ可达230的华裔数学家陶哲轩Terry Tao,对这类世界难题岂能等闲视之。然而几十年辛勤的投入,相对百年的求证,还是不够用,我们只好衷心期待他能最终摘冠!
其实是同一个数学问题:看看这个要求是不是太过分了?不给任何回旋余地,还想要“三点调头”?就像下图中的汽车就在平台上原地调头,恐怕只有世界上最牛B的老司机才能办得到。或者容忍非连通域,那干脆叫2个大力士抬起来掉头得了。

这个数学问题的另一层含义是,如何运筹使得完成倒相行为消耗为零的空间资源。长期被这个问题困扰的肯定是那些蜗居的人们,这就是为何岛国日本人,以及阿拉上海人等的物件收纳水平,汽车驾驶水平世界最高,被逼的啊!
遥想10多年前在国内开车,我一个新司机,不到一年的工夫,硬是把崭新的车刮蹭得遍体鳞伤惨不忍睹,每月还收到大把的违停罚款单,尽管自认为挂谷问题琢磨得很透也没卵用;自从来到地广人稀的加拿大,再也不为空间发愁,怎么方便怎么来,哪在乎浪费了多少没必要的空间,车身几年下来也没啥刮蹭。
现在来闲扯美国总统川普如何求解挂谷问题在社会学领域的拓扑。
曾经的商场成功人士,如今的美国大统领川普,也即特朗普先生,也曾对Kakeya猜想着谜。从他与陶哲轩教授去年总统竞选时的过招,隐约可见川普先生可能也是一位业余数学家。
陶教授当时直言不韪,用复杂的数学公式,证明了川普不适合干总统这个职位。川普也毫不示弱,当天就义正言辞地在twitter帐号上驳斥陶教授,并揶揄折腾这么久的陶教授,连挂谷猜想也搞不掂,真让人失望!下图复制于他的推特:
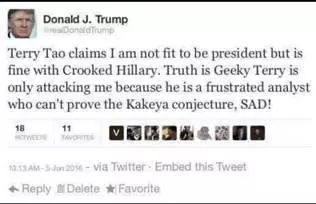
估计川普的数学演算,绝没有陈景润那样用掉几麻袋草稿纸,也许和我心血来潮那样花了一百多页A4纸,毕竟咱们都是业余爱好而已。其实我真正感兴趣的是他在开始总统生涯后,如何解决疑似挂谷猜想这类政治难题。
目前的朝核问题,对他来讲其实就是个政治意义上的挂谷猜想的求解:已知朝鲜铁定要发展成有核国家,且美国铁定不能容忍朝鲜拥核,显然这两者之间绝对对立,无任何回旋余地,如果朝鲜最后服软了弃核,或美国服软了悉听尊便,也即最终和平解决,这本质上就是求解回旋余地=0的挂谷猜想。
其实,他执政100天之内,发生很多政策180°大转弯的事情,例如从上任前指责中国汇率操纵国,到今天笑容可掬地声称中国不是汇率操纵国,并拿出中国有很多天(月)没有操纵汇率来证明其最新论断正确无比。
在北约等其它问题上,他的政策反相位计算,也只要一天即可完成。
观察他的政策倒相运算可以发现,他都是被逼得无路可走,即回旋面积=0的情况下,实现政策转向的。
深挖川普商场打拚的一生,竟然发现他真的是求解人生挂谷问题的老手。在选举互揭伤疤期间,希拉里爆料川普一生有多达6次的破产经历,而川普只承认4次而已。这破产可不是好玩的,对绝大多数人来说,那可是万复不劫的。
可是伟大的特朗普,竟能至少4次咸鱼翻身,柳暗花明又一村,最终成就今日之辉煌,这不正是求解挂谷猜想的精髓:置之死地而后生吗?呵呵,正能量满满又励志的心灵鸡汤!
再加上他一介政坛新手的身份,却能大胜老牌政客希拉里,更是其人生几何学造诣的点睛之笔。客观地讲,除了自身的实力外,我认为他还应该感谢美国的破产保护制度和选举人团制度,否则,要在中国这样的大环境,想想最近因破产导致的辱母于欢杀人案就后怕。
可见,特朗普的数学功底非常了得,日理万机中运筹帷幄达至愈战愈勇,赢多输少的局面,体现了川普品牌绝非平庸的地摊货,而是值得珍藏的高端品牌!
还有一个小小心愿:陶教授去年伤了您的心,如今您总统大位也登基了,千祈不要给陶教授小鞋穿,大度地化干戈为玉帛吧(bury the hatchet),他还眼巴巴指望今年的科研经费不要砍,以便早日攻克挂谷猜想,为美国争光。
无意置喙于其国内成绩单,那是美国人该关心的,世界人民只期待他能在当前美朝核危机的挂谷难题中求得真解,为地球70亿人带来永久的和平,特朗普,加油,为和平加油!
参考文献
1.厕所里的武士刀,你挥得动吗?http://www.guokr.com/article/68848/
2.“kakeya set” https://en.wikipedia.org/wiki/Kakeya_set
3.挂谷问题 http://baike.baidu.com/item/%E6%8C%82%E8%B0%B7%E9%97%AE%E9%A2%98
4.华盛顿邮报关于川普破产历史的文章
5.陶哲轩的博客空间:terrytao.wordpress.com
6.科学网官方微博 陶哲轩:不只是“最强大脑”
转载本文请联系原作者获取授权,同时请注明本文来自魏焱明科学网博客。
链接地址:http://blog.sciencenet.cn/blog-2339914-1049567.html






