
摘要
输配电价改革对电网项目成本核算提出了新的要求,提出一种适应输配电价改革的电网项目
成本费用核算
方法,充分考虑了新电改政策对运维成本核定的影响。根据能效理念,提出效能价值法对电网工程运维成本进行合理分摊,首先使用Lasso (least absolute shrinkage and ion operator) 算法对运维成本影响因素进行筛选,确定关键效能标准。然后对其进行赋权,从而求出单个项目运维成本分摊系数,以实现对电网项目运维成本的合理分摊。最后以某省电网工程历史数据进行实证研究,结果表明所提方法与模型对解决电网项目运维成本的分摊问题具有指导意义。
0 引言
随着《关于进一步深化电力体制改革的若干意见(中发〔2015〕9号)》和《输配电定价成本监审办法(试行)》的出台,
成本监审办法规定运行维护费要与输配电服务相关
。此背景下,对运维成本进行合理分摊就具有一定的必要性,
且合理测算电网项目的成本费用,能够实现电力改革后电网有效资产及准许成本的准确计量,为新的盈利模式下电网公司的投资转型提供支撑。
在国内外电力行业中,关于运维成本的研究大致可分为两类:基于微观经济学的边际成本法和基于会计成本学的综合成本法。运维成本作为输配电成本中重要的一部分,输配电成本分摊方法对运维成本的分摊有着重要的参考意义。诸多学者已对运维成本和输配电成本的分摊机制和方法进行了研究。文献[1]提出了一种平均增量成本年金计算方法对各电压等级本级应承担的运维成本进行计算。文献[2]提出了一种基于遗传算法和数据包络分析技术的固定成本分摊方法。文献[3]提出了一套以第三方企业为监管执行者的机制,以有效解决输配电成本核算问题。文献[4]将会计成本分摊中的阶梯分配法应用于各电压等级输配电成本分摊。文献[5]对应兆瓦-公里法提出了资金流-资金路径法对输电成本进行分摊。文献[6]基于行进路径的距离和它们在系统的每个节点上的功率注入和退出的利用程度来分配长期运维费用。文献[7]利用最小-最大算法通过实际功率追踪来解决成本分摊问题。文献[8-10]对基于比例共享的潮流跟踪方法进行了分析,并将其推广从而按用户的实际使用情况分摊运维费用。文献[11]通过计算用户收益来确定输配电成本分配,参与者收益用来计算应该分摊的成本。文献[12]围绕输电网的安全功能并结合输电冗余等物理量确定输电安全费用成本,并分摊给联网受益主体。
目前国内外电力行业在输配电成本和运维成本分摊方面的研究,主要集中在电压等级与用户方面,很少进行以单个工程为主体的运维成本分摊方法研究,不能公平的将运维成本分摊到各个工程项目,故至今尚未对运维成本的分摊形成公认的成熟理论。基于此,本文将效能的思想引入,构建单个工程与运维成本之间的关系。效能的思想是基于成员对目标的贡献度来进行分摊成本[13],可以在保证成本完全回收的同时让各方都满意地接受分摊的成本,在物流共同配送领域已得到了广泛实践。文献[14-15]根据配送企业对配送联盟运作的贡献率及通信资源使用情况建立了基于满意度的成本分摊模型。文献[16]通过对运输量等效能指标进行评价赋权,从而对配送成本进行合理分摊。
本文通过效能价值法,充分挖掘反映各项电网工程成本费用的特征参数,首先通过Lasso方法对影响运维成本的变量进行筛选。Lasso方法是在一般线性回归模型的平方误差函数基础上增加L1范数惩罚项,从而使得回归系数的求解结果稀疏化[17]。通过Lasso方法选择完变量后,再按照效能标准进行赋权,实现对电网项目输配电成本的合理分摊,并以某地区典型电网项目进行实证研究,提高电网项目经济性评价的科学性。
1 运维成本的影响因素分析
1.1 电网工程运维成本的构成
电网工程的运维成本主要包括
材料费用、修理费用、人工费用和其他费用
。
1)材料费用。材料费用是指电网企业提供输配电服务所耗用消耗性材料等费用。
2)修理费用。修理费用是指为了保持输配电相关设施正常工作状态所进行的修理活动发生的费用。
3)人工费用。职工薪酬是指电网企业为获得职工提供的服务而给予各种形式的报酬以及其他相关支出。
4)其他费用。办公费、水电费等与输配电服务相关的费用。
1.2 影响运维成本的因素分析
根据电网工程项目特点,将电网项目运维成本影响因素分为电网技术因素、社会经济因素、环境因素3类影响因素[18],具体如表1所示。
2 基于效能价值法运维成本分摊模型
2.1 效能价值法原理
效能价值法是指企业按照各项目对目标实现的贡献度或按照各部门承担的责任比重对企业总成本进行分摊的方法。
效能价值法基于电网项目实际承担的输配电任务来分摊运维成本,更能真实地反映电网工程实际成本价值
。效能价值法首先对影响运维成本的因素进行筛选,确定关键影响因素及效能标准。然后对各个效能标准进行赋权,最后通过权重计算方法得到工程运维成本分摊比例系数,从而求出工程运维成本。
2.1.1 效能标准确定
通过对运维成本与影响因素的关系进行线性拟合可以看出,运维成本中的材料费用与线路长度、变电容量等因素是具有一定的线性相关关系、修理费用与线路长度、地区生产总值等具有一定的线性关系。运维成本与部分影响因素相关关系图如图1所示。

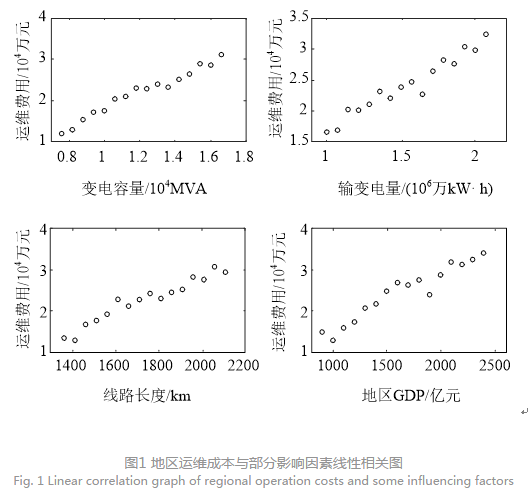
在以往的研究中,对影响因素的分析大多使用普通最小二乘法和似然估计法对模型的系数进行估计,在影响因素选择方面,大多使用逐步回归方法。但是无论是最小二乘法、似然估计法还是逐步回归法,都有不足之处,它们往往局限于局部最优解,而非是全局最优解,并且逐步回归选择的变量没有消除其严重的多重共线性问题[19],这对选择之后的工作提出了更高的要求。后来学者在研究最小二乘法的基础上提出了岭回归和Lasso回归算法,这两种算法都是在最小二乘法的基础上,通过构造惩罚函数,实现变量精简问题。虽然岭回归也能实现变量选择,构建出稳定的模型,但是在面临特征相似的数据时,只能将权重均匀赋予给这些数据,无法在构建的模型中剔除变量[20]。当需要在相似特征数据中进行选择时,这种方法就不能实现了。基于此,本文采用Lasso算法对运维成本影响因素进行筛选。
Lasso即最小绝对值压缩选择算子,该算法的思想是通过构造惩罚函数,通过控制惩罚项系数的大小,使得估计后一些变量的系数变为零,从而实现变量精简的目的。


确定运维费用的关键影响因素以后,需要确定效能价值法模型中的效能标准从而进行分摊。由于单个电网工程的运维费用不能直接得到,本文的研究目标是将地区的总运维费用分摊到单个电网工程。因此我们确定的效能标准为关键影响因素的单个工程值除以地区总值,如式(7)所示。其中,关键影响因素的工程数据值可以累加得到该影响因素的地区总值,因此各个工程项目的关键因素对应的效能标准相加便等于1,确保了地区总运维费用能够完全分摊。


2.2 基于效能价值法运维成本分摊流程
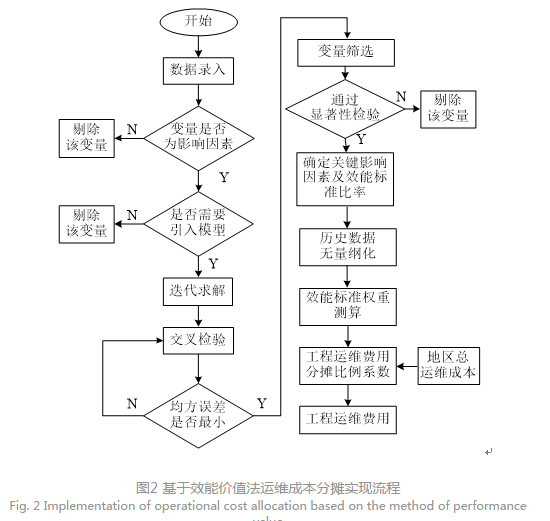
基于效能价值法的运维成本分摊流程见图2,具体如下:
1)录入数据。
2)判断录入的数据变量是否是运维成本的影响因素,剔除不是非运维成本影响因素的变量;判断剩余影响因素变量是否需要引入模型之中。
3)运用Lasso算法对输入模型的影响运维成本的因素进行筛选。首先进行迭代运算,得到获得不同取值水平下的回归结果。随后进行交叉检验,根据均方误差大小确定参数的取值,得到对应参数水平下的步数,筛选出关键变量。
4)对筛选出的变量进行显著性检验,对不能通过显著性检验的变量进行剔除,通过的变量确定其效能标准。
5)利用极值化方法对关键影响因素的历史数
据进行无量纲处理,得到无量纲数据集。
6)对无量纲数据集按照公式进行计算处理,测算效能标准的权重。
7)通过权重和效能标准,确定工程运维成本分摊比例系数。
8)根据地区总运维成本求得工程分摊的运维成本。
3 算例分析
3.1 算例数据
算例数据以某省2010—2017年的电网运营数据为研讨对象,此省包含11个地区,数据近百组,其中包括
总运维成本、输送电量、变电容量、最高负荷、容载比、可靠性、线路长度、线损率、变损率、地区GDP、固定资产、供电区域、供电面积、人口数量
等。这些数据作为Lasso方法进行关键变量筛选的基础。在指标权重确认中,选取近期的120个不同电压等级的具体分项工程的数据进行权重测算。在此基础上提出了基于效能价值法的分摊模型,并选取5个典型工程数据对上文所提出的基于效能价值法的分摊模型进行了实验研究,得到了工程运维费用分摊的效能标准及分摊比例,准确的测算出单项工程的运维费用,适合电改后电网精细化投资的要求。

3.2 效能标准确定及赋权
利用R语言对某省电网企业的历史数据进行分析,筛选出影响贡献度的关键因素。上文介绍了影响电网运行维护费的多个因素,综合考虑从中选取以下影响因素作为解释变量:输送电量(X1)、变电容量(X2)、最高负荷(X3)、容载比(X4)、线路长度(X5)、地区GDP(X6)、固定资产原值(X7)、供电区面积(X8)、供电密度(X9)、人口数量(X10)、线损率(X11)、变损率(X12)。电网运行维护费(y)作为因变量。
本文拟通过交叉检验确定λ的取值,进而得到模型选择结果。调用R语言中lars程序包实现Lasso变量筛选,得到系数解路径如图3所示。
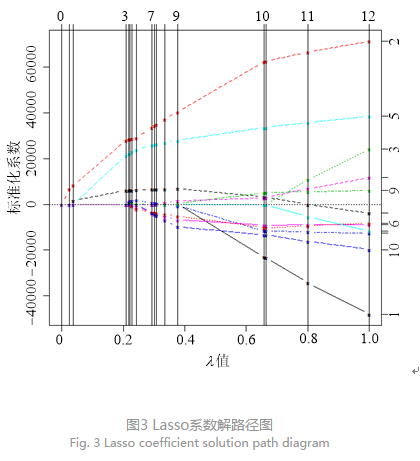
系数路径图给出了不同步数下系数增减的情况,整个过程一共进行了13步,每一步都会添加或者删除变量。在前3步,只有3个变量入选模型,随着步数增加,一些变量系数先变成零后又被赋予新的数值从而重新入选模型。在系数路径图下不能够直接看出变量筛选的结果,为进一步确定变量选择结果,采用交叉检验确定选择情况。
使用R语言编程进行计算,获取多个不同取值情况下Lasso回归的效果,通过交叉检验得到不同取值情况下均方差误差,见图4。
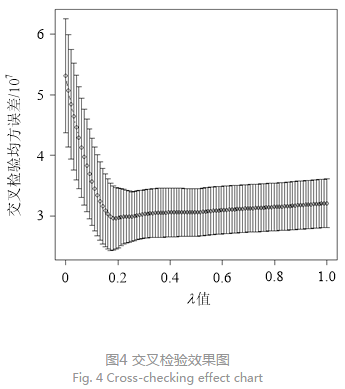
图3展示了模型预测的均方误差与λ取值的变动趋势。图中每个点都对应着一个计算结果,图的横坐标表示λ的变化值,纵坐标表示模型预测的均方误差。随着λ的增大,均方误差也发生变化,总体呈现先下降后上升的趋势。交叉检验误差值先减小后增大。当λ=0.2左右时,均方误差取得最小值,此时检验模型准确性最强。将误差最小时步数带入模型,得到筛选出来的变量如表3所示。

由表3可知,Lasso方法筛选出来的运维成本影响因素为变电容量、线路长度、固定资产原值3个指标。
用这3个自变量建立模型,并且对模型进行显著性检验,得到检验结果见表4。
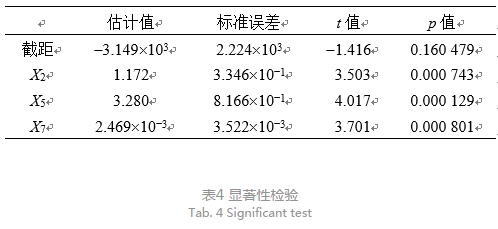
从表4显著性检验结果来看,变量X2,变量X5,变量X7的t统计量的取值分别是3.503,4.017和3.701,对应的p值分别是0.000 7,0.000 1,0.000 8。结果表示,在显著性水平α=0.05下,模型通过了显著性检验,证明了模型中的自变量与因变量存在显著线性关系。但并不意味着每个自变量都与因变量具有显著关系,因此需要对每个自变量进行回归,以决定是否作为解释变量被留在模型中。对变量间多重共线性和相关度进行检验,得到结果见表5、6。
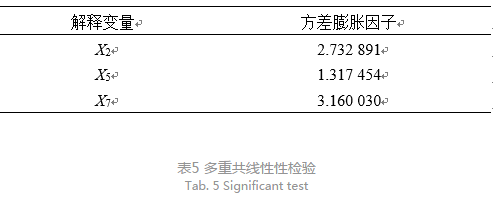
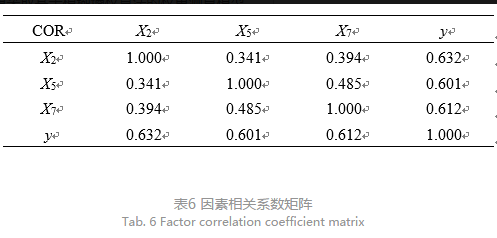
可以看出,变量X2,X5,X7的方差膨胀因子都小于10,在此情况下可以认为变量之间不存在多重共线性。表6对变量之间相关系数进行检验,结果得出,自变量之间相关系数较低,相关性较小。X2,X5,X7与y的相关系数分别为0.632,0.601,0.612,相关性较强。以上检验说明3个自变量都与因变量之间存在显著线性关系,并且通过了显著性检验。说明其是影响运维成本的主要因素。
在运维成本关键因素筛选研究中,通过运用Lasso算法对影响运维成本的因素进行筛选。最后确定变电容量、线路长度、固定资产原值各因素通过了显著性检验,证明其是影响运维成本的关键因素。
根据筛选所得的运维成本关键影响因素,因此建立效能标准为



3.3 工程运维成本分摊













