深度学习模型训练的过程本质是对权重(即参数 W)进行更新,这需要每个参数有相应的初始值。对一些简单的机器学习模型,或当优化函数是凸函数时,将参数初始化为零或者是任意一个小的随机数这种简单的方法确实有效。
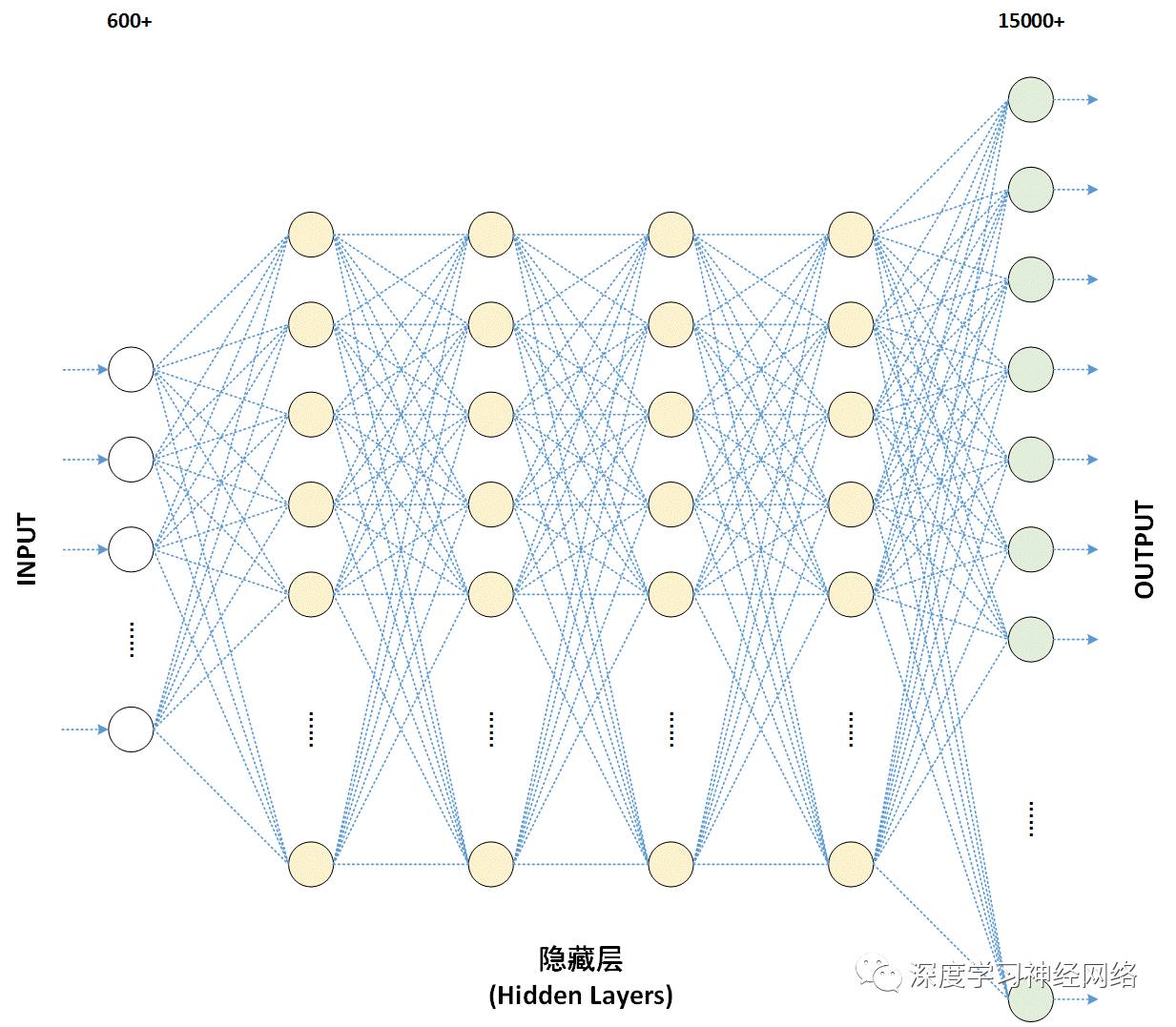
然而当搭建的神经网络层数很大时,非线性函数被疯狂叠加,如果还是使用一般的随机初始化方法,则产生的结果很不理想,下面就以下三种情况展开讨论:
1.将参数初始化为零,这种情况下,在反向传播的时候同一层内所有神经元的行为也是相同的 --- 梯度相同,权重更新也相同,整个网络是一个完全对称的网络,失去了特征提取的能力。这显然是一个不可接受的结果。
2.将参数初始化为很小的随机数字,这种初始化解决了对称的问题,在小型的网络中也适用,但会出现非均匀分布的问题。这种初始值在网络模型层数较少时,效果还是很不错的,但是随着神经网络层数的增加,梯度的输出值在与多个权值相乘后,输出的梯度值都衰减直至接近于零。
根据链式法则,梯度等于当前函数的梯度乘以后一层的梯度,这意味着前一层的梯度值是计算当前层梯度中的乘法因子,直接导致梯度趋向于零,使得参数难以被更新。
一开始数据都还是有一定标准差的,但是随着层数逐渐加深,标准差逐渐消失为0,之后神经网络的输出数据约为0,导致前向传播失败。具体来说,因为初始权重的取值太小了,导致计算是数据也变得很小,然后再往后乘上还是很小的权重,而导致最后全都变成了0。
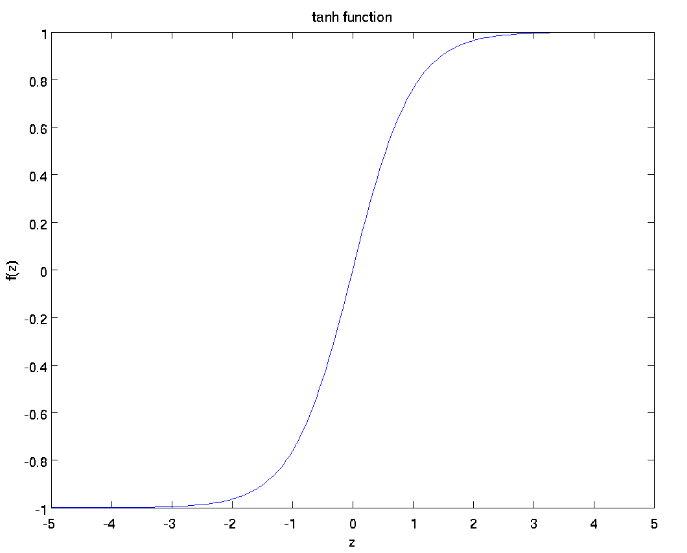
3.当权重的初始值很大以tanh函数进行举例,当权值初始值很大时,导致计算的数据也很大,从而是神经网络的每层都处于处于饱和区,几乎所有的输出值都集中在-1和1附近,神经元饱和,在-1和1附近处的梯度接近于零,梯度消失参数难以被更新。
综合对以上几种情况的考量,我们在进行参数初始化时,常采用Xavier初始化方法,这种方法的思想是保持输入和输出方差的一致。当输入的值很小时,使用比较大的权值,相反的,当输入值比较大时,使用较小的权值,这样可以避免所有的输出值趋向于零。Xavier初始化的推导过程是基于线性函数的,但是它在一些非线性神经元中也很有效。
Xavier初始化方法来源于论文《Understanding the difficulty of training deep feedforward neural networks》
Xavier初始化的实现为下面的均匀分布,上下限的系数可能因为激活函数的不同而取不同的值
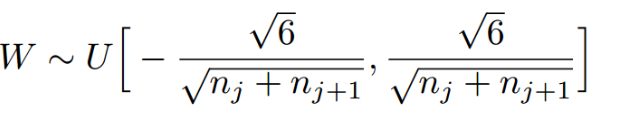
但是这种初始化方法是否对非线性函数具有普遍性呢,我们对ReLu激活函数进行考量。
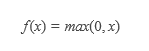
RELU函数会砍掉一半的数据,数据并非以零为中心。在这种情况下,当我们仍然采用这种Xavier初始化方法时,可以看到每一层都有大量的数据落到饱和区0处,出现梯度接近于零的情况,这显然不是我们所希望看到的。幸运的是,He initialization可以用来解决ReLU初始化的问题。
He initialization的思想是:在ReLU网络中,假定每一层有一半的神经元被激活,另一半为0,所以,只需要在Xavier的基础上再除以2。





