微信朋友圈昵称为“vick”的朋友是个爱思考的童鞋,问到了这样一道函数综合题题:

这哪是考数学啊,分明是考语文不是,文字表述好长.
的确,阅读能力也是数学解题水平的构成之一.
对待创新题要听话
分析:本题也属于创新题.在
创新题“H数列”
、
数列创新题2例
中,我们谈到解决此类问题的关键就是“听话”.
这个新定义涉及到三个函数,有了f(x)和g(x)之后,h(x)就被确定了.
我们逐一分析这三个函数.
f(x)是由对数和二次组合而成的函数,但是含有参数a,也就是说,f(x)的解析式随a的变化而变化.
g(x)就比较奇葩了:没有给出具体解析式.幸运的是,题中给出了关于g(x)的函数方程.
下面要讲一个重要技能,就是
根据函数方程求解g(x)的解析式.
常用的方法有
代换法、方程法
等.根据本题的特点,我们选择方程法.

结合选项分析,事半功倍
不要急着研究h(x),看选项.
(1)(2)都是在a=1时研究h(x)的性质,所以我们首先研究当a=1时h(x)的解析式.

下面逐一验证选项(1),(2).

接着说(3).
若函数f(x)在(0,2)上不单调,则f'(x)在(0,2)上有
变号零点.
(仔细思考上面这句话)

对勾函数的图象是双曲线
最后看结论(4).

F(x)就是我们通常所说的“对勾函数”(有的地方叫双勾函数,耐克函数,随你啦).
对勾函数的图象其实是双曲线,如果换一个角度去看的话,和我们在圆锥曲线中学到的双曲线并无二致.
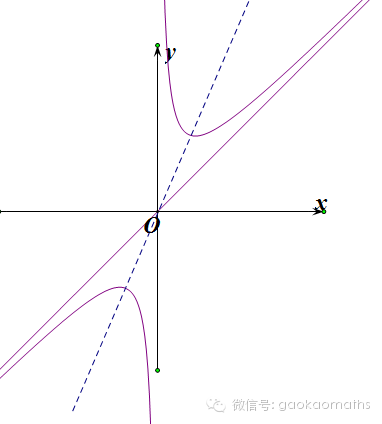
图中蓝色虚线就是双曲线的对称轴.
既然是双曲线,就有渐近线.

回到第(4)问.

特殊值法显奇功
结论(4)的意思是说,总存在满足题意的点M,N.我们不妨从特殊值出发,对b进行取值,验证几个试一试.
不妨取最常见、最简单的数值.取b=1,a=1,则函数的图象如下.
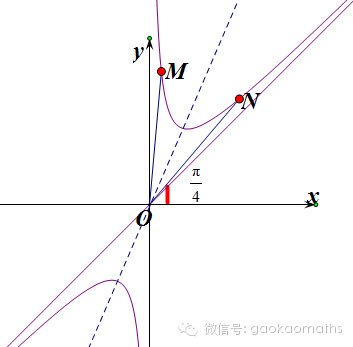
显然,当M,N不在同一支双曲线时,角MON为钝角,正切值为负值,不可能为1,不符合题意.
当M,N在同一支双曲线上时,从图能够看出,角MON始终小于π/4.
故当b=1,a=1时,不存在M,N两点,使得tanMON=b.(4)错误.
所以真命题只有1个,选A.
推荐阅读:
集合创新题,考你的逻辑思维
上一篇:
数学解题三原则
--END--
苹果手机用户专属赞赏二维码






