
作者:冯朝君,
上海师范大学天体物理中心副研究员
暗能量,之所以冠之以暗,是因为无法看到它。那么,又怎么知道它是否存在呢?实际上,人们并不知道。人们所看到的仅仅是宇宙在加速膨胀,而暗能量恰恰能合理得解释这样一种现象。于是,人们猜测宇宙中也许存在一种不明能量组分,并称其为暗能量。
在暗能量的研究中,如何将模型与观测做比较是一个非常重要的问题。本文中,我们将介绍如何使用现成的工具来完成这一工作。在这里,我们只谈及pydm软件包的使用,而不涉及宇宙学的基本知识和统计学知识。因此,对有一定基础的研究生或者高年级本科生,这部分内容是非常容易理解的。如果你不太了解相关的背景知识,请参考【天文物理】中的其他文章。
下文提及软件下载方式:
请在微信公众号:天文物理
对话框回复:pydm (即可弹出下载地址)
首先,我们的目标是根据数据得到模型参数的最佳拟合值,误差,分布以及它们之间的等高图等等统计结果。为了实现这一目标,一般需要以下几个步骤:
1.建立暗能量模型:根据研究需要,建立模型并用代码实现。这里,我们假设所要研究的是LCDM模型。
2.配置程序运行参数:包括设置哪些参数需要拟合,选用什么拟合方法,运算结果的文件名,生成图片的格式等。
3.创建主程序:调用相关模块,完成数据拟合工作。这里,我们选用的是pydm程序包,下文中会仔细介绍这个包。
我们将工作在
python
语言的环境中,
python
是一门非常简单,并且容易上手的编程语言。它的语法很简洁,初次接触它的人会觉得它有点像
mathematica
或者是
matlab
,使用起来毫不费力,非常适合科研工作,因此,有人称它为科学家的编程语言。最重要的是
python
是免费和开源的,可以为我们省下不少开销。关于
python
,不再多说什么,如果你不太熟悉它,就请去使用它吧,在用的过程中就会慢慢熟悉了。
Pydm
是一个用
python
写的程序包,你可以在本文最后找到它在
github
上的下载地址。
Pydm
包含了几个模
块:
cosmodel
,
residual
,
mcmc
和一些小工具。在
cosmodel
模块中,有一个
CosModel
类,这是一个实现暗能量模型的模板。
它本身没有做任何事情,也没有实现任何功能,它只是告诉我们需要实现哪些方法,才能完成工作。
CosModel
就好比是一个接口,如果要实现我们自己的暗
能量模型,则需要去继承这个类。
Residual
这个模块非常重要,它计算了模型与数据比较后的残差,即某个物理量的模型的预言值与观测值之差。将来用它可以计算很多东西,比如似然函数,后验分布函数等等。
Mcmc
模块中有一个类
mcmcEngine
,这个类实现了许多函数,基本上有两大功能:
1
、找模型
参数的最佳拟合值与误差,它基于两种方法
Levenberg-Marquardt (LM)
搜索算法和
Markov chain Monte Carlo (MCMC)
模拟。
2
、根据模拟结果画图,比如参数分布的直方图,散点图,等高图,可以每个参数分别绘制,也可以把它们排列成三角形。
现在,我们来构造暗能量模型。虽然这里我们只介绍了
LCDM
模型,但是,你会发现构造你自己的模型是非常简单的。
首先从
CosModel
继承一个类,我们把它命名为
lcdm
类,如下图所示:
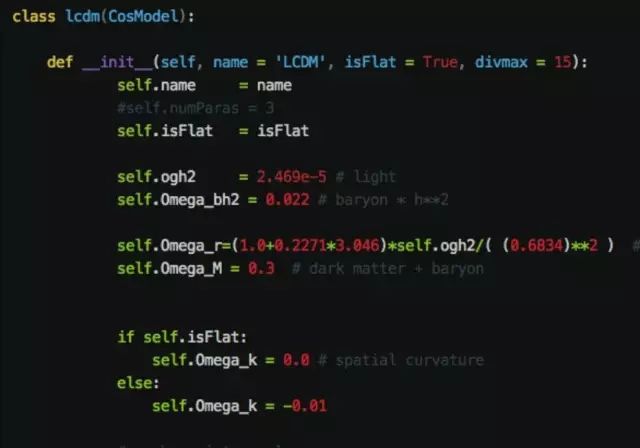
在这里,我们添加了
LCDM
模型中的参数,一旦你生成了这个类的对象,就可以在整个对象中使用这些参数,这也就是为什么我们要选择类这样一个数据类型。当然,凡是支持面向对象编程的语言都可以实现类。
接下来,要书写相关的函数。首先是
Hubble
参数,见下图:
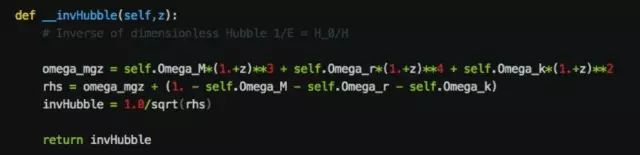
函数前面的双下划线表示该函数只能由这个类或者对象本人使用,如果是单下划线则代表它的子孙也可以继承使用。这个
__invHubble
函数的返回值是无量
纲的
Hubble
参数之倒数。由于它通常被用来作为积分运算中的被积函数,我们并不希望除这个类的以外程序来直接调用它,因此它被冠上了双下划线。另外,还要根据需要,书写一些涉及暗能量模型的函数,这里就不在再一一介绍了,大家直接看源文件就可以明白。
需要特别注意的是
paraUpdate
这个函数,见下图:
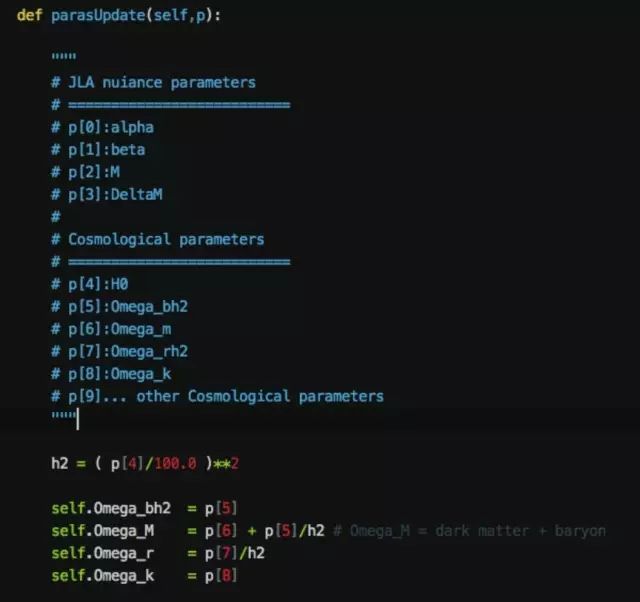
因为无论是
LM
也好,还是
MCMC
也好,都会尝试不同的暗能量模型参数,从而来计算某些量,例如似然函数的值。而这些量的值又依赖与暗能量模型本身,所以,在计算之前需要更新一下模型的参数。在这里,唯一要做的是把更新的参数
p
与暗能量模型中的参数对应起来。
首先是任务的选择:是用
LM
算法,还是
MCMC
模拟,或者两者都用;是否需要画图,见下图:
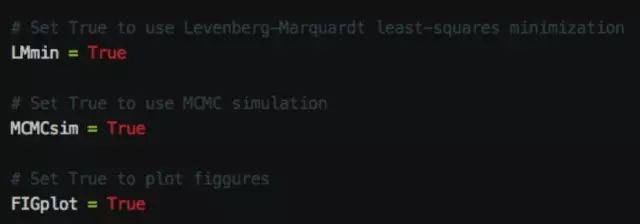
这里需要说明的是,画图是根据
MCMC
模拟生成的样本,或者是根据所保存的样本(链文件)来绘制各种图形的。所以,请根据实际情况打开或者关闭
MCMCsim
这个开关。
接下来,选择需要使用的数据。在
1.0
版本的
pydm
程序包中,已经预设了超新星
JLA
数据集,
CMB
,
BAO
的部分数据,请参考文献【
1
】。由于
JLA
的数据比较大,如果需要使用,请到
JLA
的主页上下载,然后配置相对应的目录,如下:
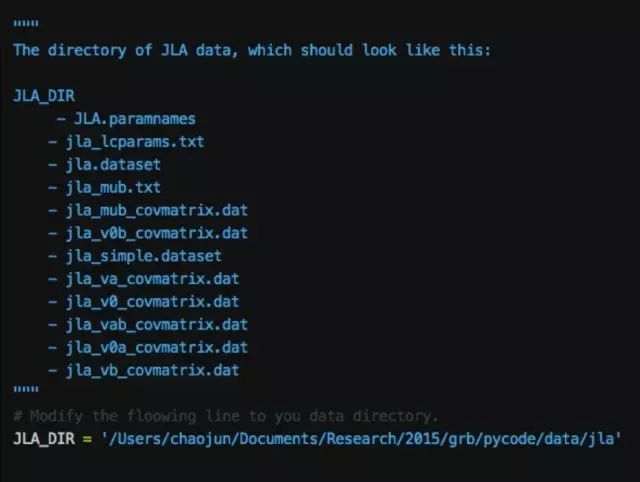
你也可以选择使用其他的数据:

当然,如果你想添加自己的数据,也是很方便的,请参考下文中的如何添加数据。
如果你需要把拟合的结果保存到文件,可以在下面设置输出的目录和文件名。目前,pydm只支持文本文件,图形文件的输出和保存,以后会逐步增加对LaTex文件的支持。
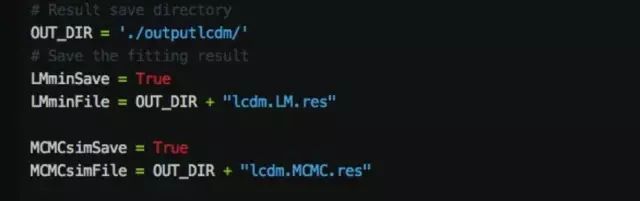
接下来这一步,比较关键。这里的iterations不用多讲,就是MCMC模拟中,循环的次数;burnIn是画图的时候用的,即忽略掉之前的 burnIn次循环,这个数值的设置没有统一说法,因为谁也不太清楚整个模拟是从哪一次循环开始进入平衡状态,即产生的样本的确是由它所遵循的分布产生的。具体应用中,可以先假设一个值画个图看看,再做调整。

这里的nwalkers是这种蒙特卡罗模拟算法中特有的,代表walkers的数量,一般设个几百就可以了,设置太多会影响到达平衡的时间,也就是burnIn就要大了,因为在该算法中,下一步的参数是依赖于上一步中所有的walker,我们会在专门的文章中介绍这个算法。值得说明的是 iterations也不需要设置太多。
在画图的时候,有三种类型的图可以选择:三角图(triangle),即把需要画图的参数,两两组合在一起,形成一个三角形状的图形;两维的直方图(hist2d),并且配上等高线;以及所有参数的直方图(hist)。你可以根据需要来选择这些类型。
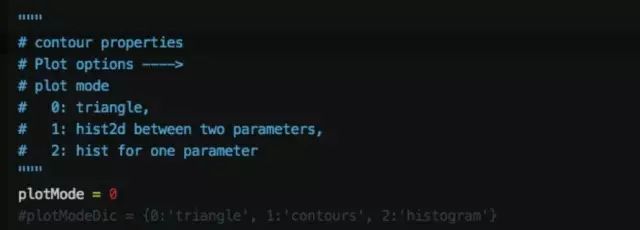
当然,关于画图还有一些其它的设置,比如颜色,光滑等等,自己试一下就可以了。在下文中,我们提供了一些画图实例,供你参考。
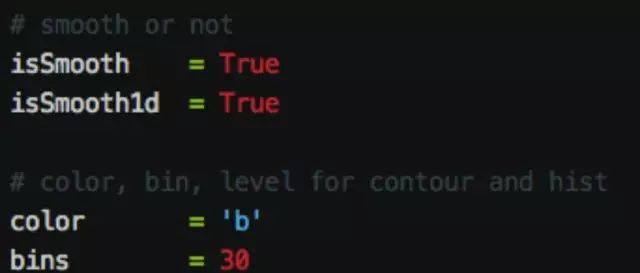
好了,现在万事俱备只欠东风了。准备充分了以后,主程序的创建其实就非常容易了。首先,需要告诉程序,你的模型参数有哪些,你可以把它们的名称写在
labelPara
这个变量中,如下:
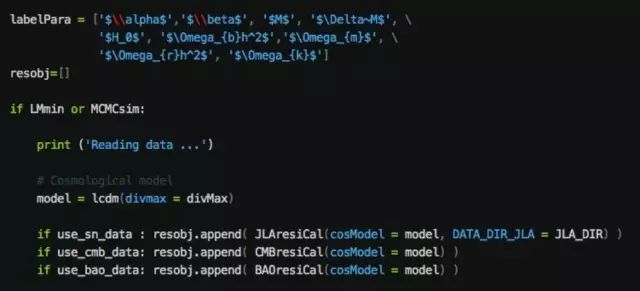
注意,写的时候可以使用
Tex
的语法,这样画图时候的坐标轴就可以显示比如罗马字符、希腊字符、上下角标等等。另外最好不要有空格出现,如果非要有,请使用~代替,比如上图中的
'$\Delta
~
M$'
。
接下来,要书写你使用的模型和数据,语法很简单,请参考上图。当然,参数的初始值、上下限也都需要设置,见下图所示:
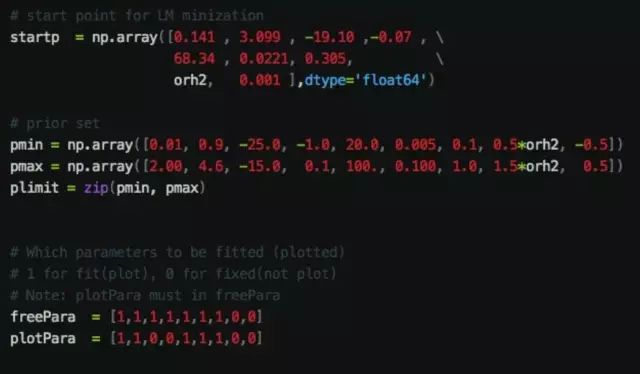
这里有两个长度相同的列表变量,freePara和plotPara非常重要。顾名思义,freePara指出哪些参数需要拟合,需要的设置为1,不需要的 则设置为0;而plotPara则告诉程序哪些参数需要画图,需要的设置为1。需要注意的是,plotPara中设置为1的参数,在freePara中也 必须为1,也就是说绘制的参数必须是拟合的自由参数。
最后一步是创建一个mcmcEngine对象,它会帮助我们完成拟合、画图的工作,见下图:
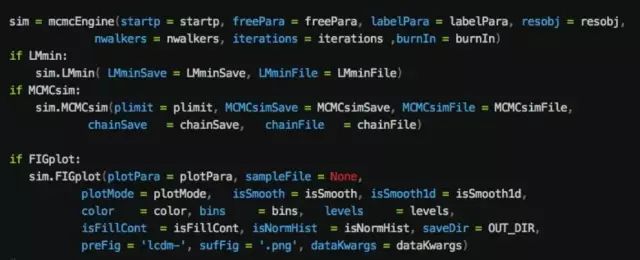
好了,到这里为止,代码的编写工作就全部完成了,接下来就运行它,获取你的研究成果吧!
当你把
pydm
软件包中的示例程序运行完,就可以得到下面几种图:
1.三角图(
plotMode=0
)
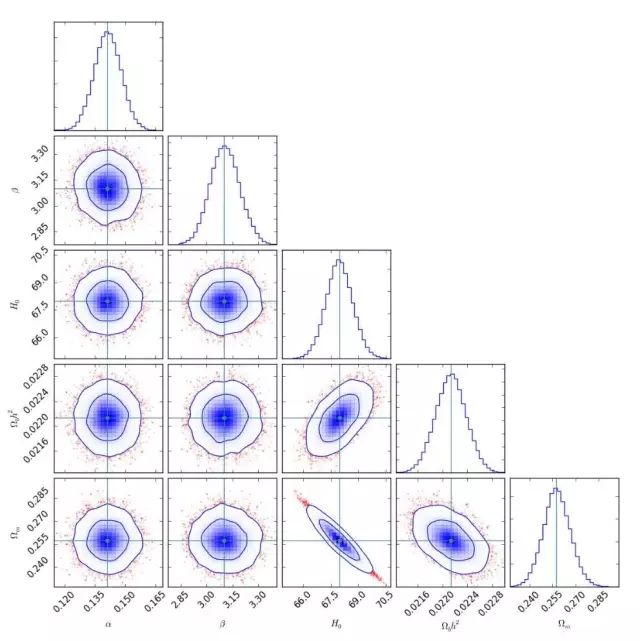
2.两维直方图(
plotMode=1
)
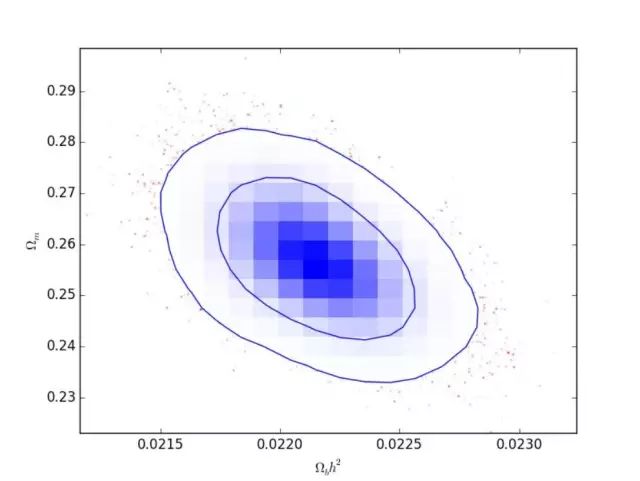
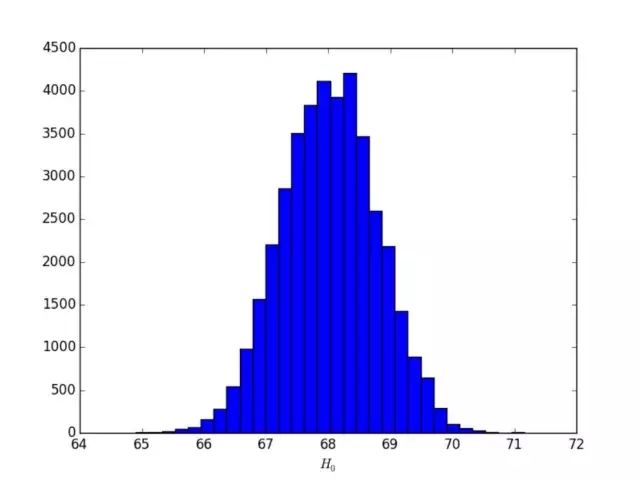
3.一维直方图(
plotMode=2
)
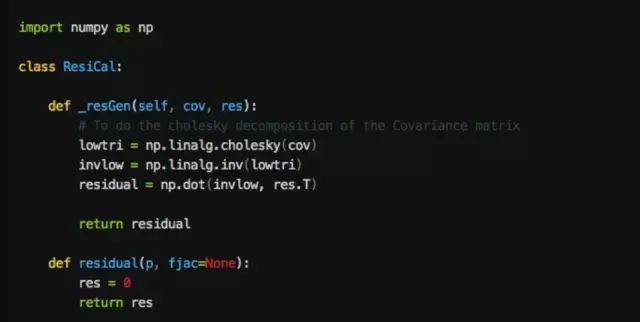
添加数据其实非常简单,只要继承
ResiCal
这个类,实现
residual
方法就可以了。这里的
_resGen
方法可以在子类中使用,它的功能主要是
Cholesky
分解。

作者:冯朝君
2009年获博士学位,师从李淼教授;
现为上海师范大学天体物理中心副研究员;
研究方向为宇宙学,对宇宙学中观测数据的处理有独到的见解,特别擅长数据分析,熟悉相关计算的软件程序;从事多年研究生的《宇宙学》课程的教学工作,其科技博文《
宇宙学还可以这么学
之基础篇
》具有广泛点击量。
上文提及软件下载方式:
请在微信公众号:天文物理
对话框回复:pydm (即可弹出下载地址)
于文末留言评论、建议、发表观点等



本文由“天文物理”载享推荐且有一定学习或参考价值、但其最终内容真实性自负。版权声明:
“天文物理”刊载此文,仅为传递更多信息之目的,文章版权归原作者或媒体所有。
本平台文章内容来源于网络且广泛…如若无意侵犯了你的权益请及时联系邮箱:bokeyuan@vip.qq.com 天文物理 将及时完善著权信息或删除等。





