【泡泡机器人好书一起读】机器人kalman教程 第1课 固定值的递推估计(下)

我们继续进入这节课的第二部分内容的学习，做好准备，我们将全面的推导卡尔曼滤波公式啦。

好吧，再次重申你叫falcao，你是一个大学生，你最大的爱好就是在你家的仓库里搞发明创造。

2.1 五个标准公式

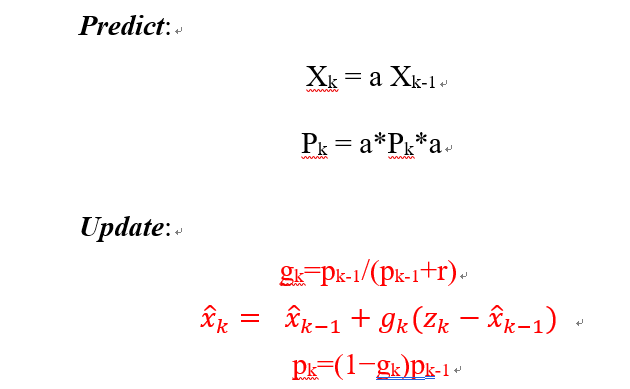
你发现对下面5个公式的推导要结合上一节课提到的批处理方法估计固定量的知识。

  回去看下上节课的内容，还记得那个著名的估计问题吗。

2.2 固定值的递推估计(上)理论推导过程回顾

即利用批处理方法估计一个固定量。

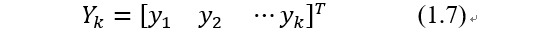
且

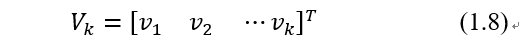
量测方程定义了误差V_k、待估计量X和量测Y_k的关系为：

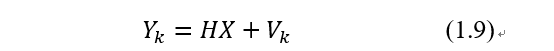
假定误差为零均值，协方差为：

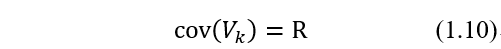
利用协方差的逆矩阵作为加权阵构造最小化函数：

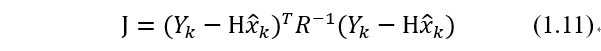
试图找到满足上式最小的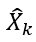。采用协方差阵的逆矩阵作为加权阵，可以增加小量测误差的影响。该问题的最小二乘解是：

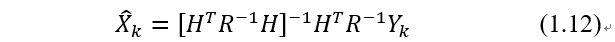
为了得到估计误差的协方差，首先将式（1.9）的Y_k代入上式可得：

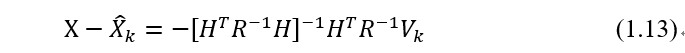
注意到误差的期望为0，对上式的外积求期望得到协方差：

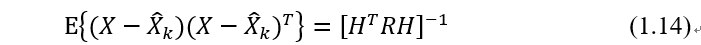
用P_k表示可得：

2.3 离散型KF推导

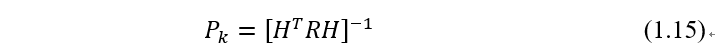
怎样把以上内容变成递推形式，让你绞尽脑汁。你跑去求助以前一起做Robocon机器人比赛的大神Dsy，你们坐下来愉快的开始了推导之旅。

要想构造递推估计，就要将量测方程改写成不同的时刻，Dsy仔细研究了式1.9，并将它改写成下表不同的公式：

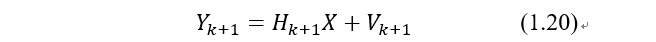
并前面构造了待最小化的函数改写为：

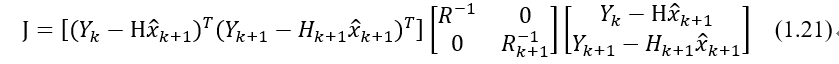
你马上打断了Dsy，“喂，这么长的公式是怎么来的啊，为什么X估计值的下标都是k+1啊？”

“哈哈，falcao，你想想我们的目的，不就是要构造递归函数啊，我们不想处理以往的数据，那就要从新息中提取信息更新当前值嘛，所以我们把X的估计用Y_k和Y_k+1两个时刻的信息进行估计，才能产生递归效果，你说对不对，还有，这个最小化函数的构造其实和批处理估计固定量的方法是一样的，都是利用R来作为加权阵啊。”

听了Dsy的一番解释，你感觉略知一二了。继续看Dsy的推导。

“同样的，我们得出1.21的解，这个和1.12其实是一样的，都是最小二乘法得出的解，如果你不了解最小二乘法，可以百度一下，10分钟就可以理解啦”。Dsy一般说一边写下了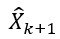的解：

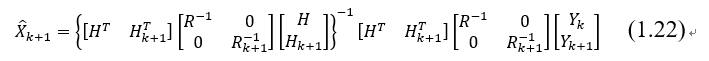
将上式化简：

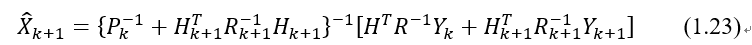
“喂喂，你又打断了Dsy，这里的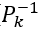是哪里来的啊？”

“公式1.15啊，我就是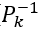代入了而已啊。不过我们确实要停一停，你知道什么是反演定理吗？”。Dsy微笑的问你。

我去，我怎么能一问三不知，哥也是机器人技术界的大神好不好，你偷偷的拿出你新买的香蕉手机，默默google。（如果你也不知道，请自己百度，很简单，打公式很累的）。

1.23式由反演定理得：

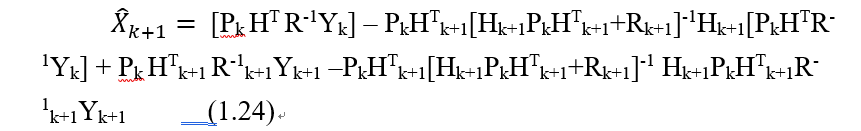
好长的公式，不过可以再化简，注意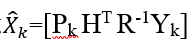，化简为：

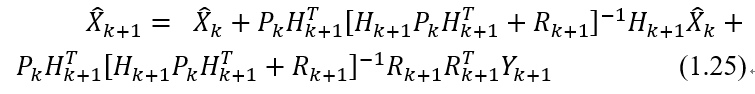
或：

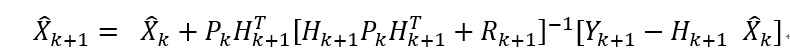
最终得到：

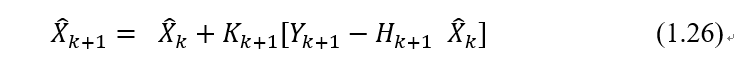
      其中：

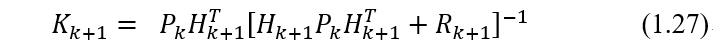       至此，新的估计值由旧的估计值加上一个修正值组成。修正值由误差项乘以最佳增益得到。这种形式直观上很吸引人，它保证了递归的效率。

你浑身轻松，并约大神Dsy一起去吃饭。Dsy笑着说，你放松的太早了，这只是固定值的递推估计，动态系统的递推估计要远远难于以上简单的公式推导。你大吃一惊，心想我怎么踩进kalman这个大坑了。后面的还会更难，这怎么解。

Dsy看你一脸迷惑，微笑的告诉你，好啦，你还没有意识到kalman的神奇作用呢，它能让你的四旋翼飞的无比的稳定，能让你的机器人小车跑得精确无误，可能让你放上天的导弹精确打击目标…….。不过我们要一步一步来，先把目前的知识搞透。

你默默的点头并对之后的动态系统状态估计充满信心。

第一节课结束了，让我们一同完成一道matlab的编程题，看看你有没有对固定量的递推估计，融会贯通。

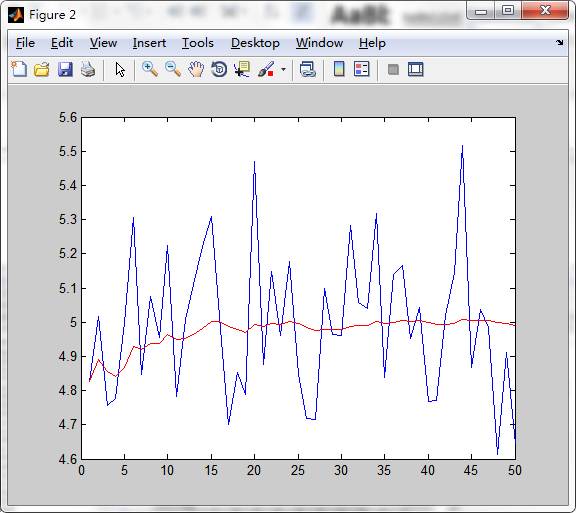
例：一个量的真实值是5.0。只采用带噪声的量测值来估计它。所添加噪声是一个均值为零，协方差为0.04的高斯白噪声。使用连续50个测量值。

/////////////////////////////////////////////////////////////////////////////////////////////////

R = 0.04;

P = R;

y(1)=5 + sqrt(R) * randn;

xest(1) = y(1);

for i = 1:49

    y(i+1) = 5 +sqrt(R) * randn;

    P = 1/ ((1/P) +(1/R));

    K = P/(P + R);

    xest(i + 1) =xest(i) + K*(y(i+1) - xest(i));

end

figure

plot(y)

hold on

plot(xest,'r')

   /////////////////////////////////////////////////////////

【版权声明】泡泡机器人SLAM的所有文章全部由泡泡机器人的成员花费大量心血制作而成的原创内容，希望大家珍惜我们的劳动成果，转载请务必注明出自【泡泡机器人SLAM】微信公众号，否则侵权必究！同时，我们也欢迎各位转载到自己的朋友圈，让更多的人能进入到SLAM这个领域中，让我们共同为推进中国的SLAM事业而努力！

【注】商业转载请联系刘富强（[email protected]）进行授权。普通个人转载，请保留版权声明，并且在文章下方放上“泡泡机器人SLAM”微信公众账号的二维码即可。  

【编辑】徐武民