在我们了解过神经网络的人中,都了解神经网络一个有很常见的训练方法,BP训练算法.通过BP算法,我们可以不断的训练网络,
最终使得网络可以无限的逼近一种我们想要拟合的函数,
最终训练好的网络它既能在训练集上表现好,也能在测试集上表现不错!
那么BP算法具体是什么呢?为什么通过BP算法,我们就可以一步一步的走向最优值(即使有可能是局部最优,不是全局最优,我们也可以通过其它的方法也达到全局最优),有没有一些什么数学原理在里面支撑呢?
这几天梳理了一下这方面的知识点,写下来,一是为了记录,二也可以分享给大家,防止理解错误,一起学习交流.
BP算法具体是什么,可以参考我上篇文章推送(详细的将BP过程走了一遍,加深理解通俗理解神经网络BP反向传播算法)。
那么下面解决这个问题,为什么通过BP算法,就可以一步一步的走向更好的结果.
首先我们从神经网络的运行原理来看,假如现在有下面这个简单的网络,如图:
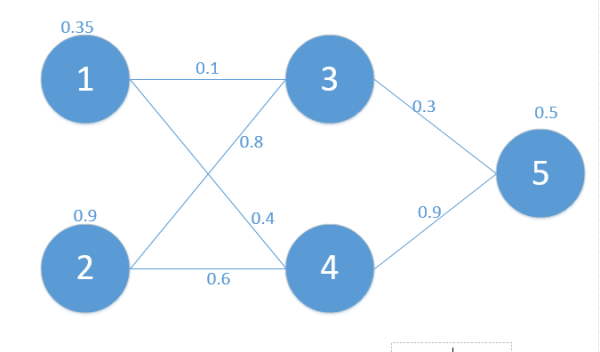
我们定义符号说明如下:
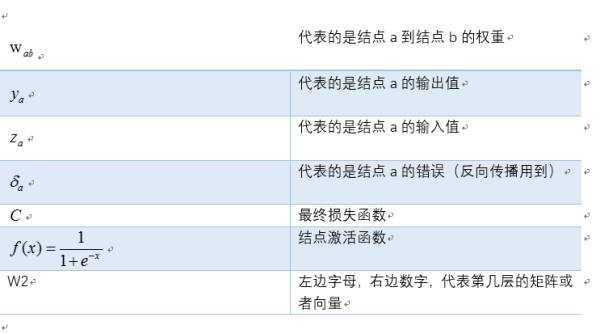
则我们正向传播一次可以得到下面公式:
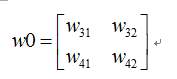
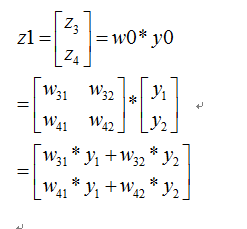
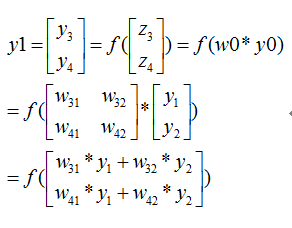
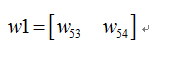
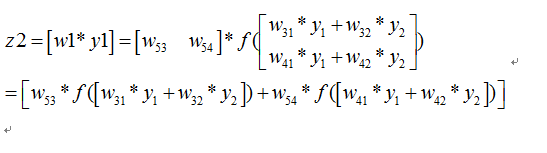
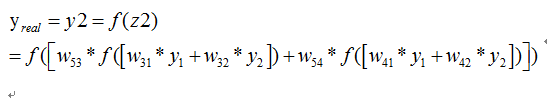
如果损失函数C定义为
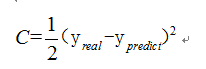
那么我们希望训练出来的网络预测出来的值和真实的值越接近越好
.
我们先暂时不管SGD这种方法(感兴趣的可以参考我的这篇文章详解梯度下降法的三种形式BGD,SGD以及MBGD),
最暴力的我们希望对于一个训练数据,C能达到最小,而在C表达式中,我们可以把C表达式看做是所有w参数的函数,也就是求这个多元函数的最值问题.那么成功的将一个神经网络的问题引入到数学中最优化的路上了.
原文链接:
https://mp.weixin.qq.com/s/r-yI7HV_dN_KaOC6mCGW-Q





