文本来自@范明非的投稿,现在看 CSS3 Transform 已经是一个老话题了,温故而知新,当然如果你还不了解的话,那千万不能错过本文。
前言
CSS3 中使用 transform 可以对元素进行变换。其中包含:位移、旋转、偏移、缩放。 transform 可以使用 translate/rotate/skew/scale 的方式来控制元素变换,也可以使用 matrix 的方式来控制元素变换。
比如:
class="box">
通过transform属性进行变换。
首先演示使用 translate/rotate/skew/scale 的方式:
.box {
width: 100px;
height: 100px;
background: #00C487;
transform: translate(10px, 20px) rotate(30deg) scale(1.5, 2);
}
也可以使用 matrix 的方式:
.box {
width: 100px;
height: 100px;
background: #00C487;
transform
: matrix(0.75, 0.8, -0.8, 1.2, 10, 20);
}
查看demo
Matrix 的中文是矩阵,是一个数学术语,在计算机科学中,会用矩阵来对象量进行变换,在 CSS3 的 transform 属性中,可以使用矩阵对图像进行变换。
矩阵长什么样子?
矩阵可以分为一个形容词+一个名字,矩是形容词,阵是名词。
如果你喜欢看战争片,不管是古代战争还是现代战争,都需要有阵势,打仗没阵型,等于耍流氓;或者是开一局农药,可能也要考虑各个英雄的站位,各种球类运动、各种棋类都需要有阵型。
阵型中的每一个个体对整体的都会产生影响。比如打王者荣耀射手时候,射手应该猥琐在一个位置输出,站错位置,输掉整个游戏。

那,其实矩阵就是一些列的数字按照矩形排列。
在数学中,矩阵用方括号包裹起来。
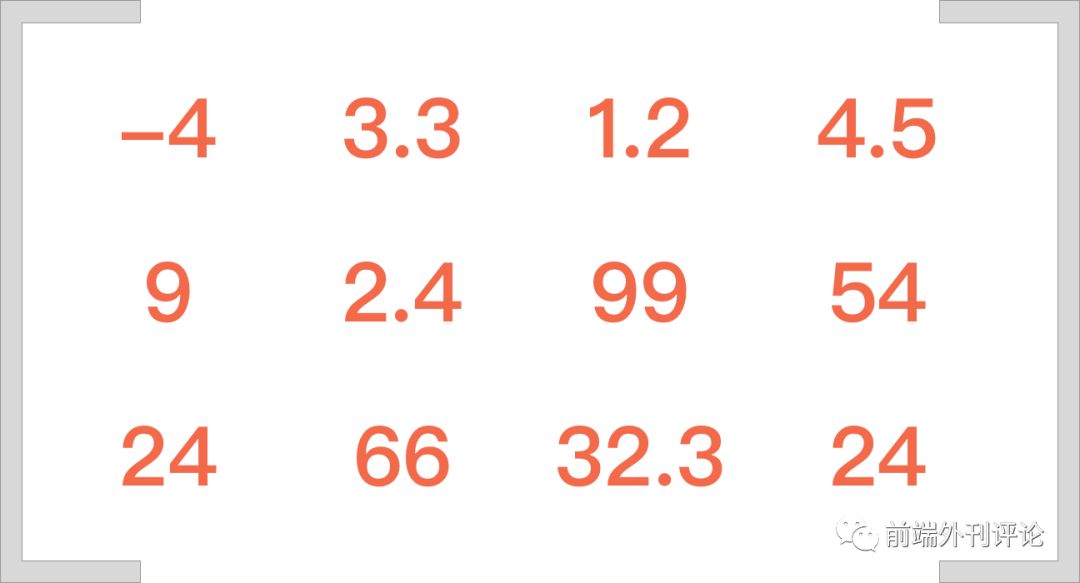
上图就是一个矩阵。
CSS3 里的 matrix 如何和矩阵对应呢?
为什么要用矩阵来表示转换呢?因为在计算机科学中,矩阵可以对向量进行转换。矩阵中的每一个数字,对向量的转换都会产生影响。
CSS3 里面可以用矩阵表示 2D 和 3D 转换,这里只讲 2D。
selector {
transform: matrix(a, b, c, d, e, f);
}
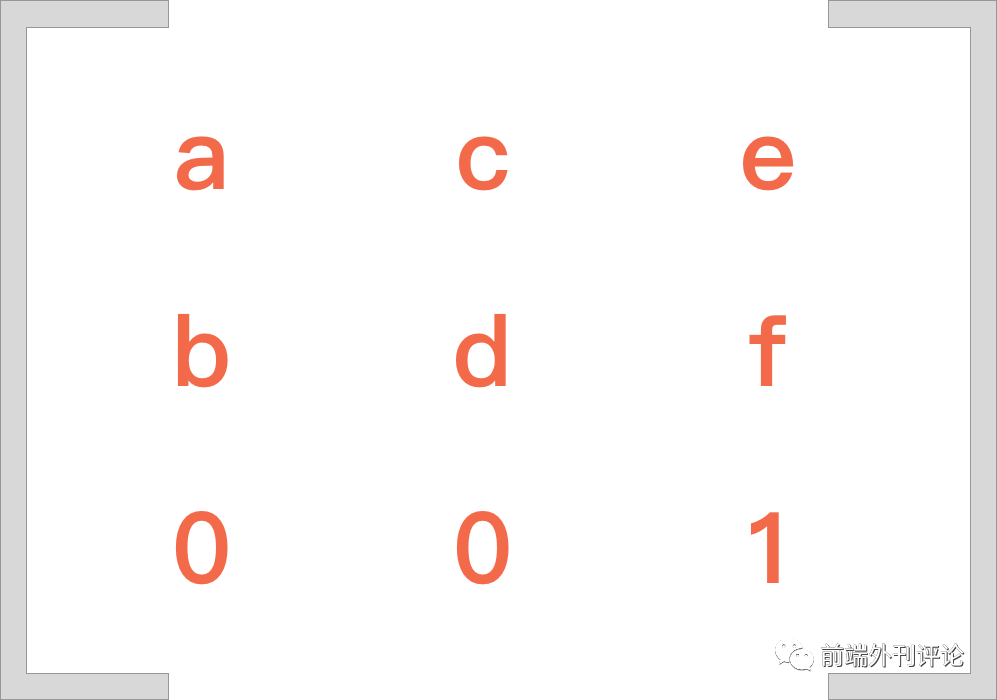
2D 的转换是由一个 3*3 的矩阵表示的,前两行代表转换的值,分别是 a b c d e f,要注意是竖着排的,第一行代表 x 轴发生的变化,第二行代表 y 轴发生的变化,第三行代表 z 轴发生的变化,因为这里是 2D 不涉及 z 轴,所以这里是 0 0 1。
假设一个问题
创建一个宽高为 200px 的div,div 里面有一个红色的点,位置是
{
x
:
181px
y
:
50px
}
。

倘若将这个div 向右平移 10px,x 轴向下平移 20px,旋转37°,x轴缩放 1.5 倍,y 轴缩放 2 倍:
transform: translate(10px, 20px) rotate(37deg) scale(1.5, 2);

那么红色点的变化后的位置在哪里呢?
既然我们知道矩阵可以对向量进行转换那么我们只要把上面的信息转换成矩阵信息,通过矩阵信息可以将我们的原始坐标转换到新的坐标。
缩放 scale(x, y)
缩放对应的是矩阵中的 a 和 d,x 轴的缩放比例对应 a,y 轴的缩放比例对应 d。
transform: scale(x,y);
a=x d=y
所以 scale(1.5, 2) 对应的矩阵是:
transform: matrix(1.5, 0, 0, 2, 0, 0);
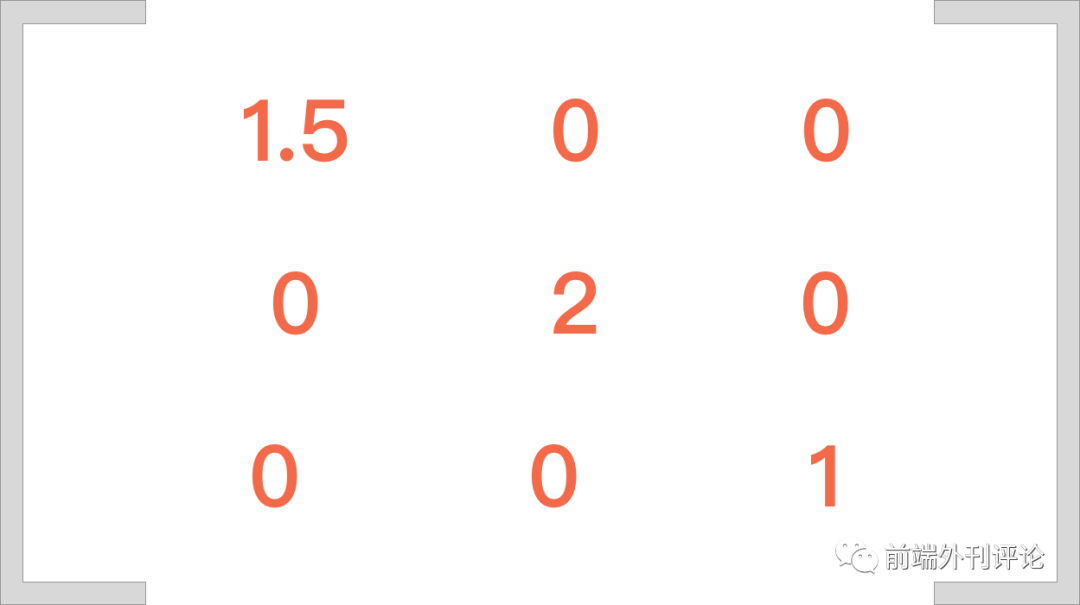
如果一个没有元素没有被缩放,默认a=1 d=1。
平移 translate(10, 20)
平移对应的是矩阵中的 e 和 f,平移的 x 和 y 分别对应 e 和 f。
transform: translate(10, 20)
e=10
f=20
对应: transform: matrix(a, b, c, d10, 20);
结合缩放: transform: matrix(1.5 0, 0, 2, 10, 20);
平移只会影响 e 和 f 值。
旋转 rotate(θdeg)
旋转影响的是a/b/c/d四个值,分别是什么呢?
transform: rotate(θdeg)
a=cosθ
b=sinθ
c=-sinθ
d=cosθ
这个是高中学的哦~
如果要计算 30° 的sin值:
首先我们要将 30° 转换为弧度,传递给三角函数计算。用 JS 计算就是下面的样子了。
// 弧度和角度的转换公式:弧度=π/180×角度
const radian = Math.PI / 180 * 30 // 算出弧度
const sin = Math.sin(radian) // 计算 sinθ
const cos = Math.cos(radian) // 计算 cosθ
console.log(sin, cos) // 输出 ≈ 0.5, 0.866
这样我们算出了 sin 和 cos,分别是 0.5 和 0.866
如果我们不考虑缩放和偏移,只旋转30°,矩阵应该表示为
transform: rotate(30deg)
a=0.866
b=0.5
c=-0.5
d=0.866
transform: matrix(0.866, 0.5, -0.5, 0.866, 0, 0);

偏移 skew(20deg, 30deg)
上面的题目中没有出现出现偏移值,偏移值也是由两个参数组成,x 轴和 y 轴,分别对应矩阵中的 c 和 b。是 x 对应 c,y 对应 b, 这个对应并不是相等,需要对 skew 的 x 值 和 y 值进行 tan 运算。
transform: skew(20deg, 30deg);
b=tan30°
c=tan20°
注意 y 对应的是 c,x 对应的是 b。
transform: matrix(a, tan(30deg), tan(20deg), d, e, f)
使用 JS 来算出 tan20 和 tan30
// 先创建一个方法,直接返回角度的tan值
function tan (deg) {
const radian = Math.PI / 180 * deg
return Math.tan(radian)
}
const b = tan(30)
const c = tan(20)
console.log(b, c) // 输出 ≈ 0.577, 0.364
b=0.577 c=0.364









