在希腊神话中，阿波罗神代表着洞见和真理，他的神殿在圣地德尔斐，阿波罗神会通过德尔斐神谕在他的神殿里向虔诚的人们预言未来。神殿的门楣上刻着一行字：“γνῶθι σεαυτόν（认识你自己）”。这句德尔斐箴言是阿波罗神告诫人类的第一句话--认识你自己--是走进神殿的第一步。
那么，对于平凡而无助的人类，如何可以认识自己呢？我们不是奥林匹斯山上的神袛，只能通过不断地自我观照，自我学习，才能从纷繁迷乱的世相中，从千头万绪的生活里，提炼自我的秉性与禀赋。这走进阿波罗神殿的第一步，已然谈何容易，从古希腊到现在，是大到人类小到己身的永恒命题，能做到者，已是圣贤了。平凡如你我，在人生的历程中反求诸己，用一生去参透，亦不知能否走进神灵的殿堂，一窥更加广大的真理。
古希腊人也许不知道，在以量子多体系统为代表的凝聚态物理体系中，也有认识自己的永恒命题，但是这样的命题，通过自我学习，也许有可能使我们登堂入室，走到阿波罗神的面前，聆听更加广大的神谕。量子多体系统中的纷繁迷乱的世相，来源于其“量子”与“多体”：唯其“量子”，对于关联电子系统的正确描述，需要遵循量子统计（费米-狄拉克或者玻色-爱因斯坦）；唯其“多体”，当我们要从统计的意义上描述体系时，系统的相空间或者说希尔伯特空间的大小，指数地随着自由度的数目增加。比如自旋为1/2的关联电子系统，相空间为4^N，其中N为电子数目，当N=100时，相空间的大小已是天文数字。希望在统计的意义上遍历相空间，严格地得到系统的配分函数，不做近似（只有可控的系统误差），这是蒙特卡洛计算孜孜以求的境界。只有不做近似，才能抓住凝聚态量子多体系统丰富的物理内涵，才能研究以量子相变和量子临界现象，拓扑相和拓扑序，高温超导体，量子自旋液体等等为代表的强关联电子系统中涌现出的奇异现象。
那么问题来了，对于凝聚态量子多体系统，蒙特卡洛模拟发展到了什么程度呢？或者说，对于强关联电子系统，（量子）蒙特卡洛模拟算法，有什么瓶颈性的困难呢？兹事体大，这里的篇幅没法完全展开，在这篇文章中，笔者只希望讲述我们最近发展“自学习蒙特卡洛方法（Self-leaning Monte Carlo method, SLMC）”三部曲[1,2,3]，讲述我们如何通过自我观照、自我学习蒙特卡洛构型，设计出自学习蒙特卡洛方法，解决了凝聚态量子多体系统蒙特卡洛模拟中一些诸如临界慢化和接收概率低等瓶颈性的问题，推动领域的发展。
对于一大类凝聚态量子多体系统，蒙特卡洛计算的效率很低，这样的情况包括在临界点附近的临界慢化，在阻挫磁体中复杂而难以遍历的低能构型，亦包括玻色子、费米子系统中的多种相互作用而导致的计算复杂度大等情况，这些情况即使得普通的蒙特卡洛局域更新策略束手无策，也使得高效的集团更新方法扼腕叹息。以描述磁性相变的伊辛模型为例，
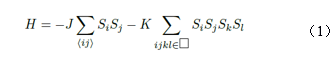
在二维的square lattice上，第一项描述伊辛自旋之间的最近临铁磁相互作用，对于这样的问题蒙特卡洛模拟可以完美求解：如果系统不在相变点上，局域的更新已经可以毫不费力的算出配分函数，从而得到各种热力学观测量。如果系统处在从高温的顺磁态到低温铁磁态的相变点上，局域更新遇到了临界慢化的 阻挠，使得真正统计独立的蒙特卡洛自旋构型不容易得到。临界慢化是指蒙特卡洛构型之间的关联随着系统尺度的增大而指数增大的现象，可以用自关联时间
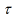来描述，在这里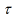正比于L^2.2，L是square lattice的线性尺度。也就是说，系统尺度越大，蒙特卡洛生成的自旋构型之间越关联，得到的结果越偏离统计独立的意义，越不可信。为了解决这样的问题，对于涨落强烈的临界点，人们设计出了非局域的集团更新，通过构建包含多个自旋的集团，同时翻转整个集团中的自旋构型，能够使得翻转之前和之后的构型统计独立，从而可以在一定程度上克服临界慢化（比如在二维伊辛模型的相变点，使用了集团更新后，构型之间的自关联时间变成L^0.2）。集团更新之所以有效，正是因为其通过对于系统自旋构型的自我观照、自我学习，设计出的更新策略体现了对于系统自旋构型的正确认识。在相变点上，自旋构型涨落强烈，自旋关联长度发散，系统中具有很多同样自旋指向的集团，在各种长度尺度上存在。集团更新的办法，就是通过判断最近临自旋之间相对指向，考虑是否将两个自旋囊括到集团中，然后再接着判断和已有集团相接的自旋，尝试将其囊括，逐渐生长出去。集团的涨落，正是系统在相变点上临界涨落的体现，算法的设计抓住临界点上的物理本质。
但是，如果再考虑模型H中的第二项，问题就又变得复杂了。第二项是多体相互作用（这里是square lattice上的四体相互作用），在实际的材料中多体相互作用普遍存在，但是对于上面讨论的集团更新策略，它却是灾难性的，因为集团更新是以两体相互作用为判断依据的，在多体相互作用下没法做集团更新，原来系统中的临界慢化，接收概率低等等问题会已更加严重的形式出现。那么如何是好呢？这里，正是自学习蒙特卡洛出场的地方。先来讲讲三部曲中的第一部[1]。
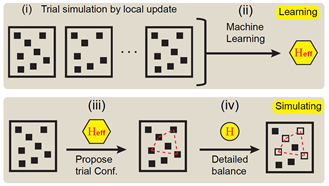
图1：自学习蒙特卡洛路线图。(i)，使用传统的更新办法生成足够多的蒙特卡洛构型。（ii）,观察构型，用自学习的方法，从现有构型中拟合出有效模型，有效模型描述系统低能的物理，比原始模型易于模拟。(iii),对于简单的有效模型，可以做集团更新，克服了原始模型的临界慢化等问题。（iv），将对于有效模型的更新反馈回到原始模型，其接收与否由细致平衡条件控制，这样一来保证了模拟的严格性（文献[1]）。
自学习蒙特卡洛第一部：
经典体系([1])
解决之道还是要通过自我观照、自我学习，学习体系的自旋构型。虽然现在的模型不能进行普通的集团更新，但是我们总是可以用局域更新的办法对其进行模拟（起码在远离相变点的地方），总是可以通过这样的模拟生成足够多的合理的蒙特卡洛构型，然后再来观察这些构型，我们意识到，这些合理的构型，总可以认为是一个有效模型Heff通过蒙特卡洛模拟而生成的，
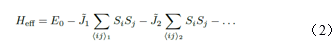
这个有效模型Heff比原始模型H简单，只包括两体相互作用。那么既然我们手头上已经具有足够多的原始模型H的构型，何不就用这些构型对于有效模型Heff做一个拟合，对于每一个构型，要求
因为构型足够多，我们总能以很高的置信度得到拟合参数，也就是有效模型中的自旋相互作用参数
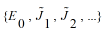的具体值。这里所说的，其实就是图1“自学习蒙特卡洛路线图”中的(i)和(ii)。 有了有效模型Heff中的参数，因为其只有两体相互作用，我们可以放心大胆地在它身上运用集团更新的方法，模拟有效模型，这样一来，临界慢化和接收概率低等等问题就有希望被克服，就是图1中的(iii)。那么到底能否被克服呢？我们来看图1中的(iv)，这里我们运用细致平衡条件，把有效模型的更新反馈给原始模型，在原始模型眼中，将自旋构型A更新到自旋构型B，这个动作会以多大的概率被接收，要看如下公式，
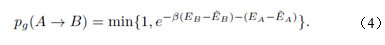
接收概率P(A->B),实际上要通过构型A和B之间的能量差来就决定。如果不做自学习，E(B)-E(A)可能会是一个很大的数，造成exp(-beta(E(B)-E(A)))很小，故而接收概率很低；但是我们自学习蒙特卡洛的妙处，就在于即使E(B)-E(A)很大，但是只要有效模型拟合得足够好，
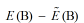可以很小，同理，
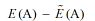也可以很小，故而
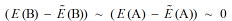,接收概率P(A->B)~exp(0)~1，总是接收。这样一来，自学习蒙特卡洛即通过有效模型的集团更新克服了原始模型在相变点处的临界慢化，又通过有效模型是原始模型的低能近似的事实，保证了近乎完美的接收概率。
效果如何，请看图2，这里我们画出对于Eq.(1)中的模型，取参数K/J=0.2, L=40时,在其顺磁到铁磁的相变点上，系统磁矩的蒙特卡洛自关联函数。横轴是蒙特卡洛的步数Delta t，自关联函数随着Delta t 衰减越慢，说明构型之间的关联越强，自关联时间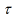就越大。我们看到，在这里，如果运用局域更新原始模型 H(Local)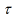，起码是400步蒙特卡洛的量级，这是典型的临界慢化；如果运用集团更新原始模型H(Naive-Wolff)，虽然好一点，但是因为对于H中四体相互作用K 项集团更新无法照顾到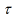，仍然是200步蒙特卡洛的量级；只有用到了自学习蒙特卡洛(Self-learning)，因为既有有效模型的集团更新，又有近于1的接收概率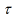，降到了15步蒙特卡洛，比局域更新加速了24倍。这正是自我观照、认识自己，无往而不利。
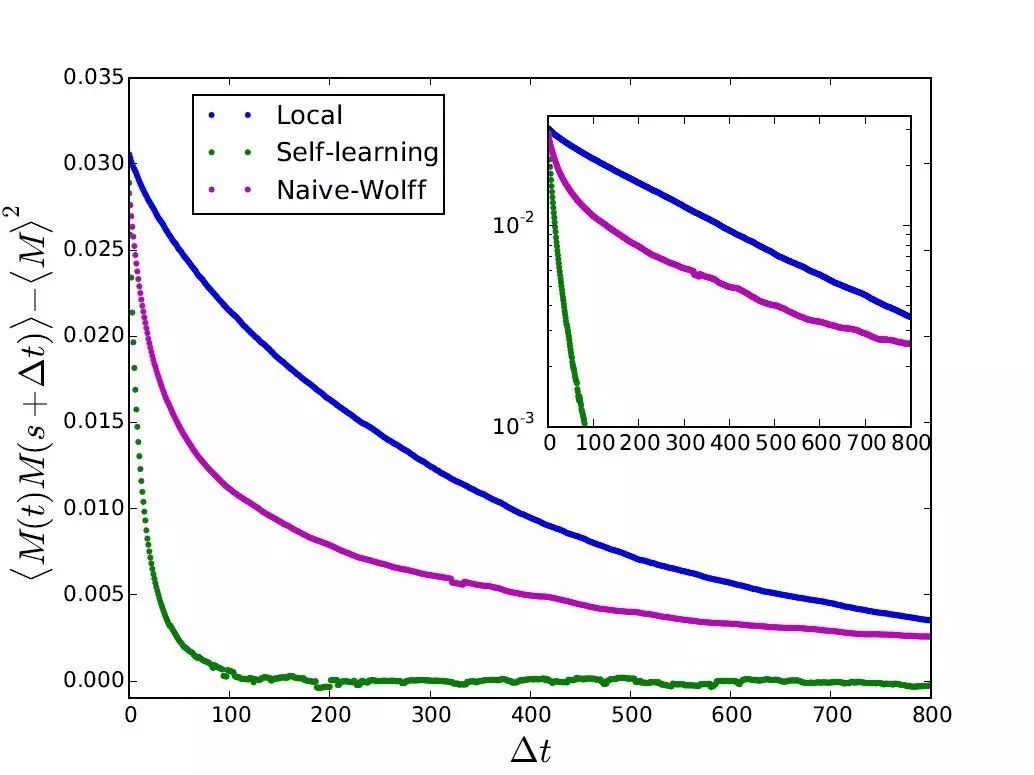图2：自学习蒙特卡洛在经典系统中的结果。对于Eq.(1)中的模型，K/J=0.2, L=40,在其顺磁到铁磁的相变点上，系统磁矩的蒙特卡洛自关联函数。Delta t 是蒙特卡洛的步数。Local 是用局域更新计算原始模型H的结果，明显地看到临界慢化；Naive-Wolff 是用集团更新计算原始模型H的结果，由于四体相互作用K项集团更新无法照顾到，仍然明显地临界慢化；Self-learning是用自学习蒙特卡洛计算的结果，因为既有有效模型的集团更新，又有近于1 的接收概率，自关联时间明显减小，加速24倍（文献[1]）。
文献[1]中的模型稍嫌简单，虽然自学习方法的思想已蕴藏其中。故而，在三部曲的第二、第三部（文献[2],[3]）,我们将自学习蒙特卡洛推广到更加复杂但是更加贴近凝聚态量子多体系统实际的模型里，取得了很好的效果，下面简要描述之。
自学习蒙特卡洛第二部：
费米子体系中的自学习蒙特卡洛([2])
依前所述，“量子”特性导致了蒙特卡洛方法对凝聚态多体系统的统计性质的研究更加困难，而费米子的泡利不相容原理则进一步使得对费米子体系的研究雪上加霜。蒙特卡洛的基本特性是按照体系特定的概率分布进行抽样，也就是基于构型相应的权重（能量）来实现在相空间的行走，从而实现构型的更新。对于经典体系或者玻色子体系，对于给定构型，计算相应的权重可以在一个常数时间内完成，即计算时间不依赖于体系的尺寸，但是对于费米子体系，同样的计算所需要的时间则按照体系尺寸的三次方增长。这样的特性导致对于费米子的蒙特卡洛研究变得极其困难。而我们提出的自学习蒙特卡洛方法则可以很 好的克服这个困难。利用自学习蒙特卡洛方法，我们用一个有效的波色子模型来代替原来的费米子模型，更好地指导构型在相空间的行走。具体的做法是，利用有效模型进行很多步的相空间的局域行走之后，把得到的新构型作为原始模型的试探构型，再使用细致平衡条件，使得试探构型以很高的概率接收，从而及其高效地实现原始模型的构型更新。
如果把费米子体系蒙特卡洛的计算比作商品销售，传统的方法是我们需要开车拉着所有商品（原始模型）挨家挨户推销，而挨家挨户寻找客户（不停的局域更新构型）和实际售出商品（得到统计独立的新构型），都需要把所有商品从工厂配送到客户家中，消耗是一样的，而且是极大的浪费；而新的方法则是通过在销售过程中自我观照，自我学习，训练出一只精干的市场调研小分队，寻找潜在买家（高权重统计独立的构型）的工作只需要派出这只消耗极低和效率极高的小分队（有效模型），达成购买协议之后再由运输部门实际配送货物（是否接受找到的新构型）。显而易见，新的方法通过自学习训练有效模型并据此指导构型更新，而有效模型的构型更新又十分的廉价和迅速，从而可以极大地增加蒙特卡洛的实际运行速度，可以实现对更大体系的模拟研究。我们把有效模型指导下的连续不断的更新称为cumulative update（累积性更新）。
这种结合累积性更新的自学习蒙特卡洛方法可以通用地适用于所有费米子体系，也包括同时具有费米子和波色子相互作用的体系。并且对于尺寸越大的体系，增速的效果越明显。我们基于双交换模型，进行了新方法的测试。如图所示，对于8×8×8大小的立方晶格中，新的方法可以轻松达到上千倍的加速效果。
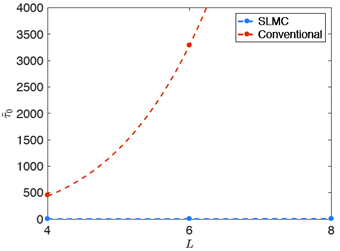
图3：自学习蒙特卡洛在费米子双交换模型中的结果。传统方法（Conventional）和自学习蒙特卡洛（SLMC）对于双交换模型在不同大小的立方晶格中的效率比较。横轴是三维立方晶格的尺寸（L×L×L），纵轴是以费米更新步数为单位的自关联长度，正比于得到两个统计独立的构型所需要的实际计算时间。显而易见，对于传统方法，随着体系尺寸增大，需要的计算时间指数上升；而对于自学习蒙特卡洛，计算时间几乎不依赖尺寸，而且远远小于传统方法。更重要的是，尺寸越大，加速倍数也越大（文献[2]）。
自学习蒙特卡洛第三部：
自学习行列式蒙特卡洛([3])
巡游费米子的量子临界性质是强关联电子领域的一个重要研究课题。巡游费米子量子临界点在很多过渡金属氧化物、重费米子等材料的超导、非费米液体等行为中扮演重要角色。由于问题的复杂性，以微扰论为代表的解析方法，无法给出定量正确甚至是定性正确的结果，近年来量子蒙特卡洛方法的发展使得数值求解这一类问题成为可能。例如，我们考虑一个描述金属中的Ising铁磁量子临界点模型，其中金属中的Ising铁磁量子临界点通过玻色场与费米面的耦合引入，利用行列式蒙特卡洛（Determinantal quantum Monte Carlo, DQMC），我们可以数值求解这个模型。但是，我们发现常规的行列式蒙特卡洛算法在相变点上会遭遇严重的临界慢化问题。此时，利用自学习蒙特卡洛方法就可以彻底解决这个困难。图4显示的是在有限温度的Ising铁磁相变点上，常规行列式蒙特卡洛（DQMC）与自学习行列式蒙特卡洛（Self-learning Determinantal Quantum Monte Carlo, SLDQMC）的构型之间的自关联时间随着系统线性尺度（L）的变化。
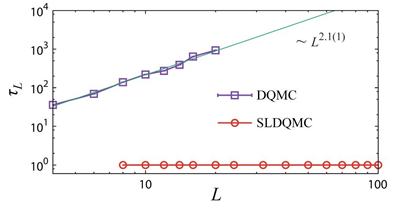
图4：自学习蒙特卡洛在巡游关联电子系统中的结果。如果使用常规行列式蒙特卡洛（DQMC）,由于算法只能使用局域更新，其构型之间的自关联时间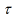~L^2.1, 这是典型的临界慢化；使用自学习行列式蒙特卡洛（SLDQMC），归功于累积性更新和理想的接收概率，临界慢化被完全消除。而且，计算的复杂度被降低，使得原本无法企及的系统尺度100×100变得可能模拟（文献[3]）。
在图4中使用了对数坐标，横轴是系统线性尺度，纵轴是蒙特卡洛自关联时 间，可见，自学习行列式蒙特卡洛（SLDQMC）方法的蒙卡自关联时间不依赖于系统的线性尺度，临界慢化问题得到根本解决。更有意思的是，计算复杂度也被大大降低，在特定温度下，SLDQMC和DQMC相比，可以得到N倍的加速（N=L×L是二维晶格的大小），从而使得我们可以计算二维L=100这种费米子量子蒙特卡洛计算中前人无法企及的系统尺度。
结语
通过自学习蒙特卡洛三部曲，从经典系统[1]，到巡游费米子与经典自旋的耦合（双交换模型）[2]，再到巡游费米子的量子多体系统[3]，我们一步步地看到，自学习蒙特卡洛比传统的蒙特卡洛方法大大前进了一步。通过观察蒙特卡洛构型，用自学习的方法，可以拟合出描述系统低能物理的有效模型，相比于原始模型，有效模型易于模拟，而且可以通过对于有效模型的累积性更新，克服临界慢化的难题；更有意思的是，我们可以善用细致平衡条件，使得通过有效模型对于原始模型的更新，保持近乎完美的接收概率。由于这两个优势，自学习蒙特卡洛可以极大地减少计算复杂度，在困难的凝聚态量子多体问题中，获得上千倍的加速。比如在第二和第三部中，对于相互作用的费米子体系，100×100的晶格已变的可以模拟，这是领域内期盼多年的结果。对于凝聚态量子多体系统中的一些基本问题，现在有望给出更加确定性的回答。
时光再回到古希腊，德尔斐箴言——“认识你自己”，这句在人类文明的孩童期就提出的永恒命题，似乎还会永恒下去。平凡如你我者，只有在不断追问、上下求索的过程中，籍心于能够走进神殿，聆听阿波罗的真理，然而这谈何容易。但是，往往就是在追问的时候，偶尔的灵光一闪，可以让我们在自己的领域里参透一些幽深的真理，片刻地走入神灵的殿堂，自学习蒙特卡洛与其在凝聚态多体系统中的应用，是为一例。
参考文献：
[1]. Self-Learning Monte Carlo Method, Junwei Liu, YangQi, Zi Yang Meng, Liang Fu,arXiv:1610.03137[cond-mat.str-el].
[2]. Self-Learning Monte Carlo Method in Fermion Systems, Junwei Liu,Huitao Shen, Yang Qi, Zi Yang Meng,Liang Fu,arXiv:1611.09364[cond-mat.str-el].
[3]. Self-Learning Determinantal Quantum Monte Carlo Method, Xiao Yan Xu, Yang Qi, Junwei Liu,Liang Fu, Zi Yang Meng,arXiv:1612.03804 [cond-mat.str-el].
致谢：
完成这三部曲的团队，除笔者外，还包括物理所许霄琰，麻省理工学院刘军伟、戚扬、沈汇涛、傅亮。其中刘军伟和许霄琰更对本文“自学习蒙特卡洛第二部”，“自学习蒙特卡洛第三部”的文字，有直接贡献，这里一并感谢。我们这个团队，配合默契，在地球的两端共同认识彼此、认识自己，收获地不仅是有趣有益的物理。
另外，笔者尤其要感谢的，是我在物理所优秀的同事王磊。广而言之，自学习蒙特卡洛是机器学习的观念在凝聚态多体问题中的具体应用，正是王磊满怀激情地“鼓吹”和潜移默化地“渗透”，让笔者开始注意到这个方向，原来一些模糊的想法开始被具体化。在运用机器学习优化蒙特卡洛算法方面，王磊与合作者（黄理、杨义峰）也有不凡的工作，arXiv:1610.02746[physics.comp-ph]，arXiv:1612.01871[cond-mat.str-el]，与自学习蒙特卡洛类似的想法，也在其中闪烁着。
编辑：杨发枝
近期热门文章Top10
↓ 点击标题即可查看 ↓
1. 如果再读一次研究生
2. 13张图，带你认识大学各专业
3. 你以为你很懂水？
4. 拿过奥运会奖牌的数学家，数学博士答辩时却坐满了他的球迷
5. 磁场的本质是什么？|No.32
6. 广义相对论和狭义相对论的根本区别 |No.31
7. 物理天才马约拉纳消失之谜
8. 研究量子场论的 也许是这个星球上最聪明的一群人
9. 他是中科院超牛的物理学者，更是摇滚界无人不知的“李白”
10. “逗妹纸”的16种用法 | 线上科学日
点此查看以往全部热门文章
