* 本文节选自《数学女孩4：随机算法》第1章，[日]结诚浩著，江志强译，2019.05出版。
我这是在哪儿？
这里是大陆还是小岛？
这里有没有人居住？
这里有没有野兽的威胁？
我，还什么都不知道。
—《鲁滨逊漂流记》
1.1 掷骰子
两个骰子
“我们来比赛吧，哥哥！”尤里叫我。
“好啊，今天比什么？”我回应道。
“我来出题，咱们认真地决一胜负吧！”
掷骰子比赛
爱丽丝和鲍勃各掷一次骰子，掷出点数更大的一方胜出。那么爱丽
丝获胜的概率是多少呢？
正值四月，每天都是温暖惬意的日子。此刻我和尤里正在我的房间里。
表妹尤里住在我家附近，上初二——啊不，从今年春天开始就上初三了。也许是从小就经常一起玩耍的原因，她都不叫我“表哥”，而是直接叫我“哥哥”。她扎着马尾辫，头发是栗色的，穿着薄毛衣和牛仔裤。
每逢休息日，尤里都会来我的房间玩。最近我们经常在一起思考数学，解数学题。
“呃 …… 因为对称性
（对称性是说爱丽丝和鲍勃在比赛中的地位相同，谁也不比谁占优势，所以获胜的概率相同。但此处主人公大意遗漏了平局的情况，因此得出了错误的结论。——译者注）
，爱丽丝获胜的概率不就是
嘛。”我回答说。
“错——啦——”尤里露出十分开心的表情。
“啊，不对。两个人——”
“你漏掉了两个人平局的情况。”尤里接过我的话。
“是我大意了。”我说道，“爱丽丝的骰子的点数有 6 种，与之相对应，鲍勃的骰子的点数也有 6 种。也就是说总共有 6 × 6 = 36 种情况。这 36 种情况中每一种情况发生的概率都相同。”
所有情况数 = 爱丽丝的 6 种 × 鲍勃的 6 种= 36 种
我看着点头的尤里，继续解释。
“36 种情况中，爱丽丝和鲍勃的点数相等的情况有 6 种，此时结果为平局。所以能分出胜负的情况就是 36 − 6 = 30 种。这 30 种情况中，一半，也就是 15 种情况下爱丽丝获胜，其余 15 种情况下鲍勃获胜。”
“嗯嗯。”
“所以，爱丽丝获胜的概率就是这样的。”我接着说。
“这次答对啦。爱丽丝获胜的概率是
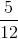。哥哥，你漏掉了两个人平局的情况，没想到哥哥也会犯这种低级错误喵～”尤里用猫语说道。
“我也会有失手的时候呀。”
“遇到复杂的问题应该‘用表格来想’，这可是哥哥你告诉我的。”
“确实是这样啊。”竟然因疏忽大意而犯了低级错误，我有些不甘心。
“用图来表示
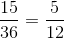的话 …… 看，就像这样。”
“嗯 …… 那该我出题了。”我的语气有点强势。
“真是的～你都高三了我才初三，别这么认真啊。”
抛两枚硬币
爱丽丝抛出百元硬币和十元硬币 A 各一枚后说：“两枚硬币中至少有一枚是正面的。”
此时，两枚硬币都是正面的概率是多少呢？
译者注：这里的百元硬币和十元硬币指的是日本货币。日本货币中的硬币有 1 日元、5 日元、10 日元、50 日元、100 日元、500 日元六种面值。
“是吗？”
“我们已经知道至少有一枚硬币是正面的了，对吧？也就是说，两枚硬币是否都为正面，由另一枚硬币是否为正面决定。那么，概率不就是
嘛。”
“然而错了。概率为
是错的。”
“诶！？”尤里似乎打心眼里吃了一惊，“这不可能！”
“可能。”
“不可能！”
“分析概率问题时，要注意‘观察整体’。”
“绝对是
的嘛。”
“尤里，你在听吗？”
“听着呢，刚刚说要观察整体对吧？”
“对于这个问题，我们要解决的是百元硬币与十元硬币的正反面问题。”
“这个 HH 是？”尤里问我。
“这个啊，H 表示正面，T 表示反面，它们分别对应英文 Head 和Tail。Head 和 Tail 虽然是‘头’和‘尾’的意思，但是也能用来表示硬币的正面和反面。”
“哦哦，我才知道。”
“抛出百元硬币和十元硬币时，发生 HH、HT、TH、TT 这四种情况的概率相同，对吧？”我问她。
“是的。但是 TT 这种情况是不可能的呀，不是已经知道有一枚硬币是正面了嘛。”尤里回答道。
“说得没错。因此，实际上只有 HH、HT、TH 这三种情况中的一种会发生。”
“啊 ……”
“HH、HT、TH 这三种情况中每一种情况发生的概率都是 1/3。其中，两枚硬币都是正面的情况只有 HH 一种。综上所述，所求的概率是 1/3。”
“嗯嗯 ……”沉浸在思考中的尤里，栗色的头发闪耀着金色的光泽。
“正确答案是 1/3。明白了吗？”
“哥哥，爱丽丝说了什么来着？”
“爱丽丝说‘两枚硬币中至少有一枚是正面的’。”
“我明白了！‘至少有一枚’才是关键。爱丽丝口中那枚正面的硬币，可能是百元硬币，也可能是十元硬币，有两种情况。”
“嗯，说得对。至少有一枚硬币为正面的情况有三种。其中两枚硬币都为正面的情况，只有 HH 一种。但是只有一枚硬币为正面的情况却有HT 和 TH 两种。”
“原来如此啊。”
“刚才我也说过了，分析概率问题时一定要注意‘观察整体’。”
“呜喵！”尤里猛地伸了个懒腰，“我玩腻了。我们抛真正的硬币来定胜负吧！借我一个百元硬币。”
尤里刚接过我递出的百元硬币，便用大拇指将其向上弹起。伴着清脆的声音，银色的硬币笔直地飞起又落下。尤里伸出左手背轻巧地接住硬币，随即用右手捂住。
“尤里，厉害呀。”
“要是正面就算我赢，反面的话哥哥就输了。”
“我明白了 …… 嗯？等一下！”
“切 …… 被你发现了吗？”
“肯定会发现的吧。要是按照你的规则，尤里你岂不是百分百获胜！”
“不啊，你看，硬币要是立起来的话就是哥哥胜！”
“喂喂！”我们相视而笑。
“嘿嘿 …… 这回来真的啊。正面、反面，猜一个？”
尤里把捂住硬币的手“唰”地伸到我面前。
“反面吧。”我有点犹豫。
话音刚落，尤里就松开了手。
“真可惜，是正面。”
“诶？这可是反面呀。印有年号的那一面是反面。”
注：日本造币局规定：为方便起见，印有年号的一面为反面。
“诶诶诶？是这样吗？”
“所以说，是哥哥我赢了吧。”
“你耍赖。”尤里不服输地撅起嘴。
“一点儿都没耍赖好吧？”
“我要给耍赖的哥哥出一个难题！”
这时，从厨房传来我妈妈的声音。
“孩子们，来吃点心啦。”
“来了 — 哼，哥哥被拳击场的铃声救了呢。”
“哪有什么铃声 ……”
“这次先放你一马。”
尤里这样说着，轻快地跑出房间。
呼 ……
我四肢无力，拖着脚步跟随尤里走向餐厅。
桌子上摆放着刚做好的装在盘子里的饼干，还有盛在马克杯中的汤。
“这是什么呀 ……”我闻了闻汤的味道说。
“我用新的香料开发出的新作品呀，想听听你们的评价。”妈妈露出得意的神色。
“这味道好奇怪啊。”
“好香啊。”尤里这样说道。
“尤里真是个乖孩子。”
“呜，这个味道实在是 ……”我尝了一小口，嘟囔着。
“真没礼貌！”妈妈抱怨着，“我可是每天都做饭的人。哪像你，前几天让你做个奶油炖菜，面粉都没搅拌开，最后全都结成疙瘩了。就你这个样子，还想对我做出来的东西指指点点吗？”
“说是让我做饭，实际上是把我强行拽到厨房吧。”我反驳道，“还有，刚才明明是您让我们说感想的 ……”
“你连把所有材料搅拌均匀这点小事都做不好。”妈妈无视了我的反驳，“对了，还有元旦的时候也是，让你照看煮豆子的锅，结果煮得太久，锅都被烧糊了。”
“当时我读书读得入迷，不知不觉就忘了要关火这回事 ……”
“哥哥，你快点学会做家务吧。”尤里说道，“不然尤里也放心不下你呀。”
“说什么呢？”啊啊真是的，对话变得越来越复杂。
“这孩子有在好好教你学习吗？”妈妈问尤里。“这孩子”指的是我。
“嗯，哥哥刚刚还给我讲了概率的问题。”尤里答道。
在这种时候，尤里总是显得聪明机灵，懂得对大人露出一张爽朗的笑脸。
“说到概率，车站前在卖‘春天的彩票’呢，我看到那里贴了一张大海报。”妈妈说。
“是写着‘本店诞生了一等奖！’的海报吧？”我说道。
海报整体为手写风格，在“一等奖”三个字上面还加了“◎◎◎”这样的记号。
“那家店的中奖概率会不会比较高啊？”妈妈将信将疑。
“不，那是不可能的，妈。”我说，“可不要被‘诞生了一等奖’这种话迷惑了呀。”
“是这样的吗？可既然是中过奖的店，中奖的概率应该会高一点吧？”
“数学上没有这种说法。”
“但是，这家店也可能是被彩票女神眷顾了呀！”
“哎呀，妈 …… 彩票是没有记忆力的啊。之前哪家店中了奖哪家店没中，彩票是不知道的。别上那种海报的当。”
“但是 ……”妈妈好像还没有想通。
“哥哥。”刚喝完汤的尤里说，“海报上写的是‘本店诞生了一等奖’，对吧？”
“是的。”
“从数学的角度来看，海报上的说法也没什么不对吧。”
“此话怎讲？”不仅妈妈，怎么连尤里也这么说 ……
“就是 ……‘本店诞生了一等奖’这是事实吧，海报上也没写‘在本店买彩票会更容易中奖’啊，对吧？”
“…… 没错。”我无法否定，“这样一来，反而是购买彩票的人的错喽？是他们误会了海报的意思，是他们自作主张？这真是太狡猾了。”
“说的是呢。”
“有许多概率问题都与我们的直觉相悖。如果不仔细计算，很容易被欺骗。”
“先别在意那个了，快把汤喝了吧。”妈妈对我说。
好不容易把汤都咽了下去，我才和尤里回到房间。
“说到概率，就不得不提到
蒙提霍尔问题
了。”我说。
蒙提霍尔问题
主持人在桌子上摆好 3 个信封。
主持人：
“这 3 个信封中，有 1 个信封里装有礼品券，其余 2 个信封
是空的。那么，你选哪一个呢？”
你选择了 1 个信封并拿到手中。
正当你想要打开信封的时候，主持人示意你停下，然后这样说道。
主持人：
“我知道哪些信封是空的。作为提示，我将从桌子上剩下的
2 个信封当中选择 1 个打开。如果装有礼品券的信封还在桌子上，我就
会打开另一个空的信封；如果桌子上的 2 个信封都是空的，我就会随机
选取其中的 1 个打开。”
主持人从桌子上的 2 个信封中选取了 1 个打开。的确，那是个空信封。
主持人：
“现在你可以坚持你的选择，拿走最开始选取的信封，也可
以和桌子上剩下的信封交换。你会怎样选择呢？”
你很想要礼品券。所以，是继续选择最开始拿到的信封好，还是和
桌子上剩下的信封交换好呢？
“这是不可能遇到的场景喵。”尤里否定得毫不犹豫。
“不，这是在电视节目《一锤定音》
( 译者注：《一锤定音》（Let’s Make a Deal），斯蒂芬·豪托什（Stefan Hatos）和蒙提·霍尔（Monty Hall）于 1963 年创办 的美国电视 游 戏 节 目，蒙 提·霍尔在 随后多年（1963 年至 1986 年，1991 年）都主持了该节目。)
中实际出现过的场景。只不过，据说节目中使用的道具不是礼品券和空信封，而是轿车和山羊。”
“山羊！山羊好棒喔。我好想要啊～”
“呃，山羊是猜错的那一种啊。”
“问题叫什么来着，好像是蒙提霍尔问题？”
“蒙提·霍尔是节目主持人的名字。”
“哦哦。对了哥哥，即便主持人打开了空信封，也不会发生最开始选择的信封里礼品券消失，或者突然出现了礼品券这种情况，对吧？”
“是的。”
“这样的话，交换信封什么的不就完全没有意义了吗 …… 我明白了，这是个陷阱问题！虽然问题问的是‘你是继续选择最开始拿到的信封好，还是和桌子上剩下的信封交换好’，但是答案实际上是‘无论选哪一个，结果都是一样的’— 哥哥是想抖这样一个机灵喵！”
“你真是深度解读了呢 …… 那么尤里的答案是？”
“人家的答案是，不论是否交换，中奖的概率都一样！”
“错 — 啦 —”我模仿着尤里的语气。
“诶？怎么会错呢？”
“正确答案是，与剩下的信封交换更好。”
“诶！交换会更好吗？”
“是这样的。”
“一定？”
“一定。只要列举出所有的情况就能明白啦。我们将 3 个信封分别命名为 A、B、C，用表格来想。猜中时用‘ ○ ’表示，猜错时用‘ × ’表示。”
“嗯，确实是这样。”尤里点了点头。
“这 3 种情况发生的概率相等，都是 1/3。”我接着说，“这 3 种情况各自对应的选择方法也有 3 种。我们重新列一个表吧，给我们选择的信封
加上‘[ ]’。”
“原来如此喵～”
“一共有 3 × 3 = 9 种情况，每种情况发生的概率相等，都是 1/9。接下来，如果开始的时候你选到了中奖的信封，主持人会从剩余的 2 个空信封中选择 1 个打开，对应 2 种情况。此时，概率 1/9分为两份，每种情况各1/18 。”
“嗯嗯 ……”
“若是一开始你选到了空信封，主持人只能选择剩下的 1 个空信封打开，这只有 1 种情况，概率保持 1/9不变。因为有点难以理解，我们还是把它整理成表格。将一定会发生的概率 1，按 1→1/3→1/9→ 1/18 这样分解。”
“实在是麻烦喵～”尤里嘴上这么说着，脸却凑到笔记本前，全神贯
注地看着我新列出的表格。“然后呢？”
“然后呀，‘[ ○ ]’表示当你一直持有最初的信封时中奖的情况。”
