
图片来自:Pexels
文章转载自:AI100
>>>>
1986年,李开复博士发表在 Artificial Intelligence 期刊上的论文《评价函数学习的一种模式分类方法》详细介绍了黑白棋 AI 程序 BILL 的关键技术,该程序于1989 年获得了全美黑白棋大赛的冠军,可以说是三十年前的 AlphaGo。以下有完整论文,准备好开启严肃阅读模式:
我们向读者推荐李开复先生这篇发表于1986年前的论文。这篇文章当然对于 AI 博弈竞技这一研究方向来说具有历史价值,其严谨完备的讨论和规范的学术论文写作也堪称典范,不过我们之所以时隔31年翻译和发表此文,主要是有感于其中领先时代的思想,即使对于今天的 AI 学习者来说,也具有跨越时空的启发,绝对值得品读。
导读 | 孟岩
李开复于1983年至1988年在卡耐基梅隆大学(CMU)计算机系攻读博士学位,
读博期间他的主要研究方向是机器学习和模式识别,也就是今日大红大紫的人工智能之主流方向。
李开复的博士毕业论文是以统计学习方法来做语音识别,在当时是全球首屈一指的研究。他以及其同门师弟洪小文的研究,帮助其导师 Raj Reedy 于 1994 年获得图灵奖。
CMU 做机器学习和语音识别研究,是非常有渊源的。在人工智能学界,CMU 的名字与语音识别及自然语言理解密不可分。早在1960年代第一次AI热潮当中,CMU 就获得 DARPA 每年300万美元的拨款,荟集当时全球语音识别领域的顶级学者,投入语言理解研究项目(Speech Understanding Research, SUR)。然而在1974年 AI 寒冬中,DARPA 对 SUR 项目进展感到不满,停止拨款,遂致 SUR 项目半途而废。
但学者们在 SUR 研究期间取得的多项成果,例如隐马尔可夫模型,成为今日机器学习中多个分支的基础,亦奠定了 CMU 在语音及自然语言理解领域执牛耳的地位。而 DARPA 对于 SUR 项目的误伤,也成为 DARPA 历史上为数不多的遗憾之一。
SUR 虽去,但CMU在这个领域已经根深叶茂,此后人才辈出,群星璀璨。而那位今天在中国科技 VC 中以 All in AI 著称的投资大佬,那位在各种讲坛甚至娱乐节目中卖力甚至卖萌解说人工智能的开复老师,当年则是这群星中耀眼的一枚,是世界一流的人工智能专家。
上面这个故事是不少人都知道的。
但是关于李开复的 CMU 生涯,还有一个比较少人知道事情。李开复在读博期间,除了把统计学习方法开创性的用来进行语音识别,还把它用来搞了一个黑白棋(Othello)人工智能博弈程序 BILL,并且顺便拿了一个全美冠军。拿冠军这事发生在1989年,而这篇论文1986年表在AI领域顶级期刊 Artificial Intelligence 上,已经把日后冠军BILL 来了个CT式曝光,所以这篇文章的事后诸葛亮的标题可以是《一个国家冠军的诞生,以及一场事先声张的棋盘谋杀案》。
根据作者自己的评价,此论文以及围绕 BILL 的研究工作,“应该算是第一个用正统机器学习做得对弈软件。贝叶斯学习方法至今仍被很多人使用”。我们今天能够阅读这篇论文,一窥人工智能棋盘博弈的门径。
那么这篇论文有哪些穿越时空的闪光点呢?
首先,贝叶斯学习方法的应用
。
在这篇论文写作的 1986 年,人工智能研究界的兴奋点仍然在基于规则的专家系统上,距离 CMU 另一位机器学习巨擘 Tom Mitchell 经典的机器学习教材出版还有十二年之遥,以统计学为基础的机器学习尚处幼年。
但这篇论文使我们看到,当时在 CMU 等世界顶尖的机器学习研究机构,对于相关理论的研究已经到了何等深度,实践中取得了何等突出的效果。在本文的第四部分,作者详细介绍了运用了贝叶斯方法的 BILL 3.0 如何在对抗评测中横扫人类冠军以及自己的上一代版本 BILL 2.0。
我想当年读到这篇文章的人工智能学者,都应该能够感受到这一新方法、新方向的巨大潜力。
对于搞机器学习的人来说,贝叶斯是一个绕不开的名字。贝叶斯原理以数学的形式归纳了理性人的决策过程:对一件事情事先有一个估计(先验概率),随着新的证据不断出现,不断的修正自己的估计,证据越多,估计越准。这一个简朴的思想衍生出一系列以贝叶斯为名的方法和算法,如“贝叶斯学习”、 “贝叶斯推断”、 “贝叶斯估计”、“朴素贝叶斯”、“高斯朴素贝叶斯”、“贝叶斯网络”等等。但与其说贝叶斯是诸多机器学习方法和算法中的一个,不如说它是理解机器学习的一个角度。
在机器学习领域的相当多的一部分学者,直接从贝叶斯定理出发,建构了整个机器学习领域。比如说广义线性模型,深度学习,你尽可以从几何的角度进行解释和推导,但贝叶斯学者们可以用贝叶斯概率论和统计参数估计来解释和推导整个体系,而且严丝合缝。
因此在《终极算法》一书中,贝叶斯与连接、类推、符号和进化并称机器学习五大学派。贝叶斯学派的代表人物有微软的David Heckerman,图灵奖得主Judea Pearl、伯克利大学的机器学习泰斗Michael Jordan等人。近年来贝叶斯学派势头很猛,出了几本高质量的著作,比如 Kevin Murphy的 Machine Learning: A Probabilistic Perspective,David Barber 的 Bayesian Reasoning and Machine Learning,Sergios Theodoridis 的 Machine Learning: A Bayesian and Optimization Perspective。
而早在 31 年前本文作者就将贝叶斯方法用在黑白棋博弈程序中,至少在这个领域中开了应用贝叶斯方法的先声。
评价函数的质量是棋类博弈 AI 程序的关键。一个好的评价函数,对于不同的棋盘形势和弈棋步骤能够给出靠谱的评分。以这个评分为导引,棋类博弈 AI 就能够展现出极高的水平。作者在这篇论文里详细考察了黑白棋 AI 程序的发展过程,并且点出传统 AI 的关键缺陷是线性的评价函数,进而用贝叶斯方法构建了一个非线性评估函数。
如前所述,这在当时是开创性的。显然在黑白棋的博弈中,一个优秀的评估函数理应是非线性的,因此 BILL 从基因里就优于当时其他的黑白棋 AI,也难怪三年之后能够横扫天下。
其次,开发一个博弈 AI,科学是其中一部分,工程的方面同样重要。
本文透露出来的工程细节也是令人饶有兴致的,作者使用多个 AI 程序相互对抗,并且将优胜者的参数权值拿出来增强对抗方的实力,重复多轮迭代,得到越来越强悍的 AI 程序。
如果你看到论文中的这一部分,会联想到当下火爆的生成式对抗网络 GAN 和迁移学习,内心定会有拈花一笑的喜悦。
论文所展示出来的严谨和渊博也是这篇文章的一大看点。
我在论文的第五部分看到作者为了验证多元正态分布假设时,竟然不惜辛苦的将三千盘游戏当中四项特征的分布图形一一找出。这短短的一段话、几张图背后,是多大的工作量,是怎样认真的态度!反正我读到这一段时,内心是相当钦佩的,我相信读者应该也有同感。
单从本文来说,有一个不足之处,就是对于四项关键特征的交代不完整。这主要是限于篇幅和论文主题,而并非作者自珍其密。四年后在同一期刊上,作者发表了另一篇论文,题为 The Development of a World Class Othello Program,完整解释了四项关键特征及其背后的原理。我们也找到此论文的原文,并征得原作者同意,分享给为关注此话题的读者。
阅读一篇 31 年前站在世界之巅的论文,结合当前 AI 领域的巨大进展,遥想公瑾当年羽扇纶巾,这还是一个很有意趣的体验。我们将此文精心译出,正是为了让更多的机器学习爱好者一起体验这份意趣。
以下是完整论文
▼
评价函数学习的一种模式分类方法
作者 | Kai-Fu Lee Sanjoy Mahajan
卡内基-梅隆大学计算机科学系
匹兹堡,宾夕法尼亚15213,美国
推荐人 | Paul Rosenbloom
摘要
我们提出了一种实现评价函数学习的新方法,即使用经典的模式分类法。不像其他使用ad hoc法生成评价函数的博弈法,我们的方法基于贝叶斯学习(Bayesian learning),遵循一定的规则。任何可以定义目标和应用评价函数的领域都可以应用这种方法。
这种方法有以下优点:
(1)自动并优化组合特征或评价函数的函数项(term);
(2)理解内部特征的相互关系;(3)能够从错误特征中恢复;以及(4)通过评价函数直接估计获胜的概率。我们用黑白棋(奥赛罗)游戏应用了这种算法,其结果与一种已经达到世界冠军水准的线性函数相比,取得了巨大的提升。
大多数成功的博弈程序都使用全广度搜索(full-width search),这种搜索在终端节点[1, 7, 11, 14]应用一个启发评价函数。典型评价函数的形式为:
Eval = C1 x F1 + C2 x F2 +-...+ CnxFn, (1)
其中Eval 是对棋盘局面的静态评价,它是若干特征(F1,F2 . . . . . Fn)经系数(C1, C2 . . . . . Cn)加权后的线性组合。每个特征都是对棋盘局势“优势”的明确估量。在国际象棋中,合理的特征可能为棋子数优势、中心控制以及兵形。在黑白棋游戏中,合理的特征可能为机动性、边位置和棋子中间位置。
上文公式揭示了改进全广度搜索博弈程序的三种方法:
(1) 寻找更好的搜索策略
(2) 选择更好的特征
(3) 更好地组合特征
我们认为前两种方法本身就很好理解。研究人员提出了几种新的全广度搜索策略,例如SCOUT [10]和零窗口搜索[1]。不幸的是,这些方法只有在指数搜索空间中才能恒定的性能提升[7]。选择好的特征至关重要。但是,从专业知识中导出好的特征通常并不是很难[1]。
现在,最厉害的博弈程序依赖于高速的硬件而不是新搜索算法[1,3],依赖于高效的特征分析而不是发现新的特征[1, 7]。因此我们建议,对全广度搜索和特征选择的研究已经达到饱和点,未来博弈程序的成果将在很大程度上依赖于特征组合的好坏。在本文中,我们将介绍一种基于贝叶斯学习的算法,这种算法自动组合特征。
和特征选择不同,特征组合是个非常不直观的过程。一方面,研究人员必须在多种策略之间建立一种不稳定的平衡(例如选择国际象棋中位置优势和棋子优势的权重)。另一方面,必须注意相关特征间的相互作用(例如国际象棋中的兵形和国王安全)。而且,研究人员总是会面临窘境,不是特征太少,就是特征太多(这其中包含相关特征和多余特征)。
可以自动组合特征的算法是由Samuel [12]首先提出的。他引入了一种线性评价函数学习算法,之后又设计了一种基于特征表(signature table)的非线性学习算法[13]。但是,他的算法遇到了一些问题。线性评价函数对特征间关系的理解不够充分。
![]()
![]() 特征表出现由过度量化产生的平滑性问题。
特征表出现由过度量化产生的平滑性问题。
这两种算法最大的问题是:虽然它们去除了调校系数的负担,但是却增加了新的负担,例如选择特征表结果、确定量化的范围和程度以及在学习期间选择函数调整的量和频率。调试程序所需的工作量远远超过了在专家帮助下对系数进行常规的试误法(trial-and-error)调校所需的工作量。最后,由于所需的工作量太过庞大,Samuel的算法高度领域相关。
在本研究中,我们报告一种新的学习算法。和一样,我们的算法学习将特征整合到评价中。但是,不像Samuel的算法那样,我们的算法没有平滑性问题,而且是全自动的,并且不需要进行任何调试。我们的算法基于贝叶斯学习[4]。
(1) 我们积累了大量的游戏作为训练数据。每个游戏由有两位专业玩家进行试玩。
(2) 我们根据某种标准将每个位置标记(手动或自动)为获胜或失败位置。本研究所使用的标准为游戏的实际结果。
(3) 训练程序从标记的训练数据中计算出一个贝叶斯判别函数。该函数试图识别出代表获胜或者失败位置的特征模式。已知某个位置的一组特征值,这个函数给出该位置是获胜位置的概率。
(4) 我们为游戏的不同阶段构建不同的分类器。
我们的算法有五个重要的优势:
(1) 学习过程是完全自动的。不需要调试任何系数或参数,也不需要对特征进行归一化。
(2) 假设多变量正态分布,事实证明,平方组合在训练数据上效果最佳[4]。
(3) 算法不仅考虑特征本身,还考虑他们互相之间如何共变。例如,如果使用的是两个相关特征,将不会同时把它们完全整合到评价中。
(4) 算法在评价中能够从错误信息中恢复。例如,加入一个随机特征并不会降低它的性能。
(5) 它返回获胜概率,并将其作为评价。这个评价是所有评价函数都试图模拟的评价。而且,这种评价可以确证搜索树不同层次上的数值间的比较。
我们在黑白棋游戏中测试了这个算法。我们改进了黑白棋游戏程序BILL 2.0 [7],使其使用相同的特征学习某一评价函数。由于BILL 2.0中的评价经过仔细调试,而且BILL 2.0是最优秀的黑白棋游戏玩家之一,我们预计性能只能获得适度的提升。但是结果表明,几乎从初始位置开始,BILL 3.0(使用贝叶斯学习)战胜BILL 2.0的次数是它战败次数的两倍多。
本试验的平均最后得分为37至27分。我们证明,性能的增加相当于额外使用了两层搜索。在另一个涉及黑白棋游戏问题解决的试验中,BILL 3.0比BILL 2.0多解决了11%的问题,两者都使用的是八层搜索。最后,作为衡量BILL 3.0性能的指标,BILL 3.0以56-8的分数大胜美国得分最高的黑白棋游戏玩家Brian Rose。
在第2部分中,我们将首先讨论构建评价函数的常规方法以及这些方法的缺点,重点介绍Samuel的成果。在第3部分中,我们将详细阐述贝叶斯学习和它在评价函数学习上的应用。在第4部分中,我们将提供黑白棋游戏的结果。第5部分的内容是对评价函数的贝叶斯学习的分析和讨论。最后,第6部分为一些结论性评论。
2.1.评价函数在搜索中的作用
自从纽威尔(Newell)、肖(Shaw)和西蒙(Simon)发现阿尔法--贝塔(alpha-beta)关系后,博弈程序的基本模型就几乎没有发生变化[9]。几乎所有的模型仍然依赖全广度阿尔法--贝塔搜索,而且程序仍然在终端节点使用静态评价。
由于大多数程序使用的是类似的搜索策略,评价函数在博弈程序中起着最为关键的作用。评价函数体现程序的智慧,负责区分好的棋步和坏的棋步。而且,由于大多数程序依赖评价函数进行棋步排序,所以好的评价函数得出的搜索就更加高效。
静态评价包括两个阶段:(1)评价棋盘局势的特定特征,和(2)将这些特征分数整合到评价中。特征选择是一个域依赖的任务,并且无法对其进行系统的研究。在本研究中,我们将着重探讨将特征整合到评价中这一论题。特别地,我们将在后文介绍一种自动完成该任务的算法。
通常,静态评价是一个特征的线性组合
EvaI=C1×F1+C2×F2+...+Cn×Fn (2)
其中Eval是对棋盘配置的静态评价,它是若干特征(F 1,F2 . . . . . Fn)经系数(C1, C2 . . . . . Cn)加权后的线性组合。
这个表达有两个问题。首先,它假设特征是独立的,可以将他们进行线性组合。这明显就是一个错误假设。虽然线性关系可以作为一个合理的一级近似,但是我们会在后面证明,列入非线性关系可以大幅提升性能。
事实上,我们还将证明,每对特征都在某种程度上是互相关联的。而且,通常使用ad hoc法得出系数。在很多情况下,构建函数的人借助他的领域知识猜测这些函数。即使他们的确懂行,但是由于人类从阿尔法--贝塔搜索和静态评价的角度进行思考。当构建函数的人不那么懂行时,他就会毫无思绪。这就是西洋跳棋新手Arthur Samuel编写西洋棋学习程序的最初动机。
2.
2. Samuel的评价函数学习试验
1947 年到1967年期间,Arthur Samuel在西洋跳棋上对机器学习进行了一些最早、最深入的研究[12, 13]。他的目的和本研究的目的十分类似,即已知某一棋盘局势的一组特征,给出衡量棋子位置好坏的分数。虽然他进行了很多试验,但是我们将着重介绍最为重要的两个试验:(1)通过自我模拟进行多项式评价学习,以及(2)通过book moves互相非线性特征表评价学习。在接下来的两部分中,我们将对这两个过程进行描述和评价。
在多项式评价学习中[12],Samuel安排了西洋跳棋程序的两个副本进行对抗,学习线性评价函数中每个特征的权重。其中一个程序副本Beta自始至终使用一个固定的函数。另一个副本Alpha则不断改进它的评价函数。Alpha通过将它所作的评价与更加准确的评价作对比来进行学习,后者是使用极小极大搜索得出的。如果搜索返回的数值比静态评价高得多,那么就假设静态评价出现了错误。通过减小权重来惩罚静态评价中的每个消极特征。
Alpha和Beta原本是完全相同的,Alpha不断提高自己的权重。在每场游戏结束后,如果Alpha打败了Beta,那么就假设Alpha更好,Beta采用Alpha的评价函数。相反,如果Alpha在某三场游戏中都败给了Beta,那么就假设Alpha出现了错误,然后将它首项的系数设置为0,使它恢复正常。而且,如果“Alpha的学习过程明显运行不正常”,则需通过手动干预来使它恢复先前状态。
当Alpha在多场游戏中连续战胜Beta时,这个学习算法得出的评价函数似乎趋于稳定。最终程序试玩西洋跳棋游戏的表现出优于平均水平。这个学习过程是机器学习的早期范例之一。但是,它的正确性是以几个错误假设为依据的。
这些假设中的第一个就是:
好的评价函数可以定义为独立特征的线性组合。
这个假设是不可靠的,而且在其中显得尤其错误,因为他有目的性地收集多余特征。例如,如果Samuel的学习过程考虑了两个完全相同的特征,那么就会给定这两个特征相同的权重,这会导致特征值的高估。而且,线性评价函数无法采集特征间的关系。通过重复Samuel的试验,Griffith [5]证明,通过一个极其简单的启发式棋步排序过程可以提升性能。
第二个假设是
:当搜索和静态评价不一致时,那么静态评价一定出现了错误。
虽然深度搜索一般比浅搜索更加准确,但是这种假设在几种情况下会不成立。如果某个位置出现问题,那么可能只有通过向前搜索若干层才能发现这个问题。在这种情况下,则应容许静态评价维持错误状态,因为通常我们无法将这种向前搜索的知识编码到静态评价中。而且,搜索可能会受到“地平线效应”(Horizon Effect) [2]的影响,导致生成不准确的评价。
第三个假设是:
如果发现评价函数过度乐观,则假设任何积极成分都出现错误。
这明显是错误的,因为在大多数位置上,每位玩家都在某些特征上领先对手,但是却在其他特征上落后于对手。错误的评价可能是由消极成分导致的,但是这些成分并不足够消极。仅仅检查记号是不够的。
最后,这个过程假设:
如果玩家A战胜玩家B,一定是因为玩家A的评价函数优于玩家B。
这个假设可能对于专业玩家而言是合理的,但是当新手程序互相对抗时,获胜的原因可能是:(1)更加优秀的评价函数;(2)运气(当两个玩家都不理解局势时);或者(3)对手失误。由于Samuel的程序的游戏水平相当于新手,那么它获胜的原因通常是因为运气或者对手的失误,从而导致错误的信度分配。由于多项式学习涉及爬山法(hill-climbing),所以信度错误分配的问题尤为严重。
Samuel认识到了这些问题,因此他设计了另一个学习过程,这个过程纠正了大部分问题[13]。为了处理特征间的非线性相互作用,他引入了特征表;为了处理自我模拟中的错误假设,他使用了棋谱走法。
特征表是非线性组合特征的多量纲表。每个量纲代表某种特征。在评价某一棋盘局势时,每个特征的值都用来将索引编入特征表中,对应这个索引的单元格包含评价。这个方法最明显的问题在于表会变得非常大。Samuel通过使用分层结构解决了这个问题,并且将特征分为四个一组的集合。
仅考虑内部集合间的相互作用。然后每个集合从索引单元格中生成一个数值,这个单元格的索引由四个特征值创建而成。下个更高的层级中的表使用这些数值,就好像它们是特征一样。共有四级。但是这样仍然会生成非常大的特征表,因此Samuel对特征值进行了量化。在每个最低层级的特征表中,其中三个特征的数值限制在(-1,0,1)间,剩下的那个特征的数值则限制在(- 2 , - 1 , 0 , 1 , 2)间。
这就得出了图1中的最终结构。这个结构包含883个单元格,这对于存储和训练来说都是合理的。
从棋谱走法开始训练这些单元格。我们将高手下棋所用的棋局输入到程序中。目的是使特征表学习模仿高手下棋。记下与高手所选走法的特征组合相一致的单元格的数量(用A表示),以及与高手所未选的合理走法的特征组合相一致的单元格的数量(用D表示)。实际的单元格数值通过计算(A- D)/(A + D)进行周期性更新,我们用这个数值衡量单元格遵从棋谱走法的程度。
特征表方法成功地添加了非线性学习;棋谱学习法成功地消除了自我模拟的错误假设。所得程序的性能远远优于用棋谱学习训练的线性函数的性能。
但是,特征表方法仍有一些新的问题。首先,这种方法作出两种假设:(1)棋谱走法总是最佳走法;以及(2)无任何同样好的其他走法。由于这些游戏的玩家都为高手,因此不采用失败一方的走法。
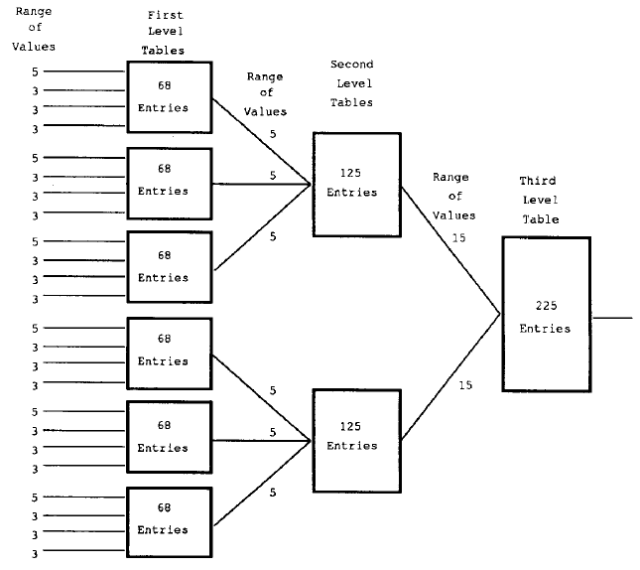
图1:Samuel最终的特征表方案
它们都是合理的假设,但是肯定不是绝对可靠的假设。通过使用足够大的训练数据集,我们可以将这些问题减至最少。
一个主要问题是,特征表在量化过程中会丢失相当多的准确性。过度量化的风险很大。例如,如果某人要将国际象棋中的实质性差异量化为3个或5个数值,那么在失去“象”和失去“后”等同时,他又怎么能预期作出正确的走法?而且,过度量化违反了Berliner的平滑性原则(smoothness principle)[2],因此引入了瑕癖效应 (Blemish Effect)。在Berliner的书中,某个特征的数值即使发生很小的改变也会导致函数的值发生非常大的改变。当程序有能力操控这样一个特征时,它就会就会运用这种能力,从而给自身带来伤害。
将特征表过度量化到少数层级也正好有这个问题。
虽然损失了平滑性,但是特征表学习仍然没有提供线性问题的通解。例如,当两个特征完全一样(或者高度相关)时,如果这些特征(F1和F2)的组合方式如图2(a)所示,那么它们在表1中的冗余度就会被成功消除。但是,如果它们的组合方式如图2(b)所示,那么F1就会编入表1,F2则会编入表2。但是,表3并不能消除它的冗余度,因为它无法知道它的两个输入是否受F1和F2或者其他特征的影响。这就导致了对这个特征的效用的高估。由于同样的原因,我们认为高层级的特征表并没有多少用处,因为它们无法识别出自身输入的贡献特征,因此也就无法处理特征表之间的关联。
因此,谨慎安排特征表的结构是很重要的,这样才能捕捉共变。而且,必须确定各级量化的范围和层次、单元格中的初始值和这些数值更新的频率以及许多其他要素。
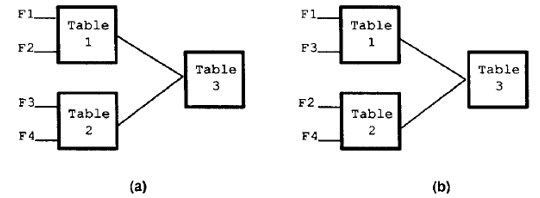
图2.如果F1和F2为相同特征,(a)中的特征表结构将会消除它们的冗余度,但是(b)中的特征表不会这样做。
这就是我们所认为的这两个过程的最大缺点,即需要进行过多的人为设定初值和干预。每个参数都增加了出现影响学习过程的人为误差的可能性,还增加了得出并测试这些数值所需的时间。结果,学习效果要么由于人为误差而很差,要么就是由于过度的人为干预而差强人意。
所有这些启发式调试使Samuel 的学习过程受领域限制。如果某人想在另一领域应用这个学习过程,那么他必须在学习算法中使用相当多的该领域的知识,并且必须在对参数进行试误法修正上花费相当大的精力。这明显很不理想。
最终,Samuel 的算法学习的概念并不理想他的自我模拟算法根据搜索学习区分好特征和坏特征。他的棋谱算法学习区分专家所选的走法和专家未选的走法。但是,在博弈游戏领域,最优的概念是学习区分获胜位置和失败位置。
总之,Samuel的研究是早期机器学习研究中的一个里程碑,我们认为,大量的监督使他的研究变得不实际并且受限于领域。这些主要缺点加上Samuel问题重重的假设、平滑性问题以及不理想的学习共同严重限制了他的学习过程的可行性和应用性。
2.3.针对自动组合特征的其他研究
Griffith最先想到特征表这个方法,他报告了大量的国际象棋评价函数学习结果[5]。他比较了线性评价函数学习、特征表学习的两种变形以及一种启发式棋步排序算法。他证明了,虽然启发式棋步排序算法只有极其基础的国际象棋知识,但这种算法的性能优于线性评价函数,却差于非线性特征表算法。
Mitchell [8]进行了另一项研究,他使用回归分析法在黑白棋游戏中创造了一个线性评价函数。得出的程序并未达到预期的游戏水平。我们猜想,这是由于(1)他的程序未使用搜索;(2)他的程序缺乏非线性特性。
这些结果都证明线性评价函数有缺陷。但是,由于平滑性问题和需要进行过多调试,特征表方法也存在缺陷。
在本部分中,我们将介绍一种自动组合特征的算法。首先,我们先向不熟悉贝叶斯学习的读者介绍这个概念,接下来再简短介绍一下黑白棋游戏和黑白棋程序BILL。最后,我们将介绍基于贝叶斯学习的评价学习算法,这种算法适用于黑白棋游戏。
3.1.贝叶斯学习
判别函数的贝叶斯学习是一种用在模式识别中的标准方法。通常,它被用于识别和分类具体对象,例如字符、图像、语音和震波。假设采用多元正态分布,判别函数定义类别间的判定边界。在双类别问题中,这条边界上的所有点属于每一类别的可能性都相同。这条边界是由训练数据的特征向量自动计算出的, 它考虑特征的方差和协方差。该边界由两个阶段构成,即训练阶段和识别阶段。
该训练阶段是一个简单的参数估计阶段。需要一个已标记训练数据的数据集。每个训练样本包含一个特征向量和一个表明特征向量所属类别的标记。训练阶段的任务是估计训练数据的每个标记(或类别)的均值特征向量和协方差矩阵。
类别c的均值向量(
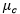 )就是每个标记为本类别的训练样本的每个特征向量的算数平均值,其计算公式如下所示:
)就是每个标记为本类别的训练样本的每个特征向量的算数平均值,其计算公式如下所示:
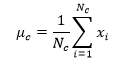 (3)
(3)
其中,
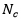 是观察类别c的次数,
是观察类别c的次数,
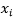 类别c的第i个特征向量。
类别c的第i个特征向量。
类别c的协方差矩阵(
![]()
![]()
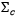 )衡量两个特征互相协变的程度,其计算公式如下所示:
)衡量两个特征互相协变的程度,其计算公式如下所示:
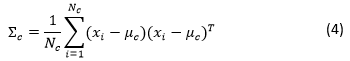
其中T是矩阵转置操作。
推导均值向量和协方差矩阵的逆矩阵公式,可得出某一分布的一般多元正态密度函数p的计算公式,如图(5)所示:
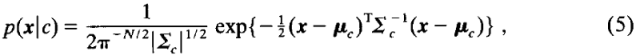
其中x是N-元特征向量,
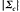 是协变矩阵的行列式,
是协变矩阵的行列式,
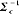 是协变矩阵的逆矩阵,
是协变矩阵的逆矩阵,
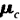 是类别c的均值向量。
是类别c的均值向量。
贝叶斯法则表明,使用判别函数
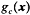 可以实现最小误差率分类:
可以实现最小误差率分类:





