对比学习是大模型的入门算法。它的想法很简单:对于输入
, 找一些它的正样本和负样本,希望在学习之后的网络特征空间中,
离正样本近一点,负样本远一点。
实际上,对比学习并非个例,预训练算法大多非常简单:要么是遮盖一部分数据内容让模型猜出来,要么是让模型不断预测一句话的下一个词是什么等等。因为这些算法过于简单,人们很难理解它们究竟如何创造出了强大的模型,所以往往会把大模型的成功归功于海量数据或巨大算力,把算法设计归为炼丹与悟性。
有没有更本质的方式,可以帮助我们理解对比学习?下面我给大家介绍一下我们最近的工作[1],可以
在不使用任何假设的情况下
,刻画出对比学习与谱聚类算法的
等价关系
。
呃……但这关我什么事?
从理论的角度来看,对比学习与谱聚类算法的等价关系是一个很优美的结果,至少我是这么觉得的——但这对大部分朋友来说并不重要。实际上,可能有一半以上的AI科研人员对谱聚类不太熟悉,对这样的理论刻画自然没有太多兴趣。不仅如此,
-
对比学习与谱聚类算法的关系
不是我们第一个提出的
。人们早就在实践中发现,对比学习得到的模型在分类任务上有突出的效果,但是在其他下游任务中表现一般。马腾宇老师组在2021年的论文[2]中极具创新性地证明了,如果把对比学习中常用的InfoNCE loss改成某种变体(他们称之为spectral contrastive loss),那么得到的模型几乎就是在做谱聚类:是谱聚类的结果乘以一个线性变换矩阵。换句话说,他们已经证明了,对比学习的变体是谱聚类的变体。我们的结果可以看作是对他们结果的进一步完善:
对比学习就是谱聚类
。因此,虽然我们的结果可以看做是这个问题的一个完美句号,但并不出人意料。
-
我们的理论框架精致,但
并非原创
。事实上,我们使用了Van Assel等人2022年发表的用于分析Dimension reduction的概率图框架[3],将其调整之后用于对比学习分析之中。虽然这一调整并不显然,相信原作者也没有想到他们的框架可以用来分析预训练模型;但是我们的理论工具确实来源于他们的工作。
所以我想,我们的工作最重要的地方是提供了
理解大模型的新视角
。对我来说,当对比学习的底层逻辑以一种简洁、优雅的方式展现出来时,它的意义远远超出了谱聚类的理论刻画本身,给我带来了巨大震撼。这种新的视角可以帮助AI从业者更好地理解预训练算法和模型,对未来的算法设计与模型应用都会有帮助。当然,这意味着要先理解一点点数学——不过我保证,这是值得的。
从SimCLR谈起
我们先从Hinton团队2020年提出的SimCLR算法[4]谈起,它也是对比学习的代表算法。SimCLR专门用于理解图像,它基于一个重要的先验知识:把一只狗的图片进行翻转、旋转、切分或者其他相关操作,得到的图片还是在描绘同一只狗。具体来说,论文中考虑了9种不同类型的操作,如下图所示:

对于人类来说,上面的这些图一看就是同一只狗。针对任何一张图片
,我们可以通过这样的方法随机生成两个它的变体,称之为
和
。既然这两个变体图片描述的是同一个东西,它们应该包含了极为相似的语义信息。可是,一只狗的像素矩阵,和将它旋转之后得到的像素矩阵,在像素空间中天差地别。那么,我们能不能找到一个语义空间,使得这两者相似呢?这就是SimCLR算法,见下图(我们基于原文的示意图进行了微小的调整)。
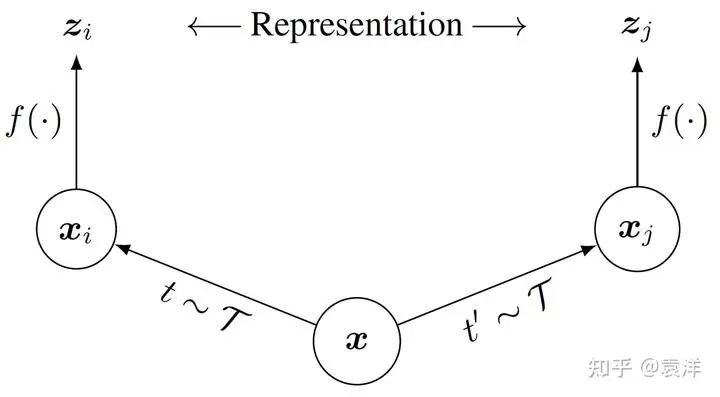
可以看到, 假如我们通过预先定义的图片操作, 生成了
和
。然后我们把它们分别塞进神经网络
中, 得到了两个向量
。我们希望这两个向量比较接近, 毕竟他们代表的图片有相似的语义。
可是, 如果使用这个标准来训练模型的话, 模型非常容易偷懒。试想, 倘若
把所有的输入都映射到同一个输出, 那自然满足我们的要求, 但是这个模型什么都没有学到。因此, SimCLR引入了负样本, 即从数据集中随机选一些图片生成
, 使得
比较近, 但是和
又比较远。这样,
就没法偷懒, 不得不认认真真学点东西了。
使用这个想法设计的损失函数叫做InfoNCE loss, 它有一个令人望而生畏的数学定义。假如给定一个图片
和它的正样本
, 还有一系列负样本, 我们叫它们
, 那么损失函数定义为 (我们进行了等价变换, 详见论文
:
这个式子很复杂,但是如果我们愿意
抓大放小
的话,它也很简单。所谓的抓大放小,就是先不管那些我们不明白的部分,只看它的主要意思。按照这个指导思想,我带着大家过一遍:
开头为什么有个负号? 说明后面的式子越大越好。为什么要加个log? 不懂, 我们先不管, 之后再说。下面这个分式是什么? 可以看到, 分子在分母中也出现了, 我们就把分子当做
的相近程度即可。分式的意思就是说,
与
这对正样本的相近程度, 相比
和
那些负样本的相近程度,应该越大越好。
为什么
能够表示两个图片的相近程度呢?
的含义很清楚, 就是把
塞进神经网络得到的表征。exp和
代表了高斯核函数, 是一种刻画两个表征的相似度的方法。。
上述就是SimCLR算法分析的传统思路。我们跳过或者模糊不清的部分,就是深度学习中非常重要的玄学——不懂没关系,效果好就行。
我们今天的目标,就是把这些部分解释清楚,同时给出一个与传统分析思路截然不同的新思路。整个故事环环相扣,我们把SimCLR算法搁置一下,先从理想空间谈起。
什么是理想空间?
我们刚才谈到,在像素空间中,模型很难理解一张图片的语义。为了能够让模型更好地理解图片的语义,我们需要找到一个更好的空间,我称之为理想空间(即刚才说的语义空间)。在理想空间里,任何两个图片的语义关系可以非常方便地计算出来。比如说,在对比学习考虑的问题里,我们可以使用一个简单的函数
直接算出
与
的相似关系。所以说,在理想空间中,图片的语义对于模型来说是“显然”的,因为任何两个图片的关系可以用
计算得到。如下图所示:
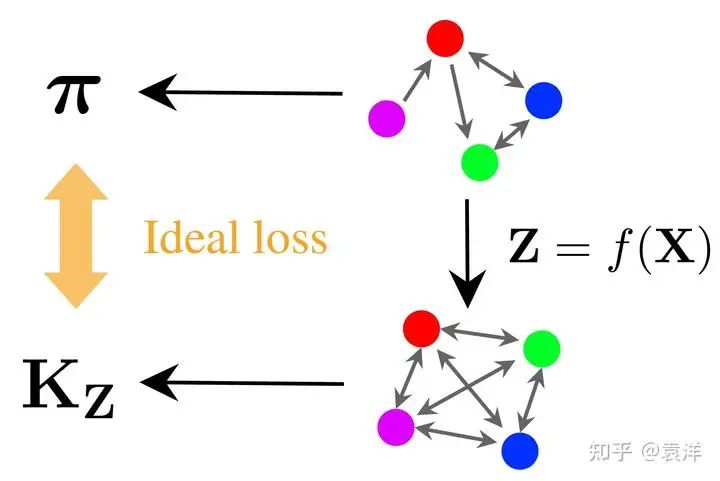
图中第一行的四个圆点表示四个数据点(在我们这里就是四个图片),圆点间的箭头表示它们之间的关系(我特意画了有向箭头,所以关系可以是单向的)。一般来说,关系可以非常复杂,但是今天我们假设两个点之间的关系可以用一个实数表示。这样,这些点与关系就形成了一个图,可以用邻接矩阵
表示。在SimCLR算法中,两个点之间的关系等价于它们被选为一对正样本的概率,表示它们的相似程度。
我们的目标是通过神经网络
计算出一个理想空间
(第二行), 使得在这个空间中, 任何两个点
之间的关系可以用一个简单的数学函数
计算得到。今天我们考虑的是一种极为简单的
函数,我们要求
可以简化写成
,即
具有平移不变性。
从图中可以看到, 我特意在任何两个点之间都画了双向箭头, 这是因为任何两个点都可以用
算出关系。这和第一行的关系图不同,因为第一行很可能存在两个点没有关系,或者只有单向关系。我把第二行的关系用邻接矩阵
来表示。
在理想的情况下,我们希望
和
是一样的。可是,如果
是对称的,而
存在有向边,那这两个矩阵完全一样是不可能的。所以, 我们需要定义一个损失函数来刻画它们的距离, 然后使用优化算法进行优化。这样,我们就得到了一个可以将对象映射到理想空间的神经网络
的算法。
然而,这个算法有个问题,就是损失函数不好算。考虑到我们的数据集非常大,可以包含几百万张甚至更多图片,所以上下两行对应的图都非常庞大,无法直接计算两个邻接矩阵的距离。那该怎么办呢?
很简单,我们可以对原图进行降采样,取两个子图进行比较。如下图所示:
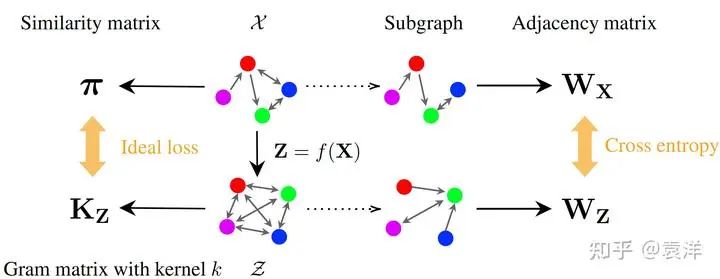
可以看到,左边计算Ideal loss可能很困难,所以我们走右边的虚线,通过子图采样的方法,得到两个子图
。通过使用交叉熵让两个子图尽可能接近,我们也可以驱使模型学习到好的理想空间。但是要注意,这个思路本质是一种启发式算法,必要但并不充分:原图一致意味着子图一致,但是子图一致不意味着原图一致。
子图采样评分
如何对原图采样呢?我们可以使用Van Assel等人提出的框架[3],使用Markov随机场。对这个工具不太熟悉的朋友不必惊慌,它背后的原理很简单。如果我们想要对原图采样(假设它有
个点),那么我们首先需要定义子图的分布。这个分布说白了,就是给每个子图一个得分,使得每个子图被采到的概率与它的得分成正比。换句话说,我们需要设计一个评分函数,用于给每个子图评分,这样就可以定义出一个采样的分布。分高的经常被采,分低的就不怎么会被采到。
所以,评分函数的定义,就决定了采样分布——我们需要设计一个合理的评分函数。我们考虑一个极为简单的办法,就是只考虑出度为1的子图。具体来说,这样的子图保持了原图的点不变,但是只给每个点留了1个出去的有向边。如果我们把这样的一个子图叫做
,那么当我们给定原图的时候(用邻接矩阵
表示),我们可以定义
的评分为:
。
注意到, 由于
每个点的出度为 1 , 所以它的邻接矩阵里面的数要么是 0 , 要么是 1 。从这个角度来看, 我们把
放到了
的指数上, 所以只有当
时
才会被计算到连乘中, 否则不会。换句话说, 当
选中的边两端的点相似度(由
定义)较高时, 评分更高, 更容易被采到。
非常神奇的是, 基于这样的采样方式,
的每一行彼此之间都是独立的, 并且每一行(因为出度为 1 , 所以有且仅有一个 1
是从多项式分布
中采样得到的。换句话说, 对于第
行的 W来说, 它的第
列为 1 的概率恰好为















