转自老顾谈几何
公众号ID：conformalgeometry
作者：顾险峰
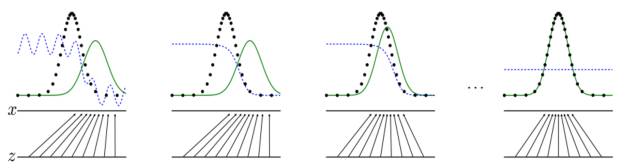
图a. Principle of GAN.
前两天纽约暴雪，天地一片苍茫。今天元宵节，长岛依然清冷寂寥，正月十五闹花灯的喧嚣热闹已成为悠远的回忆。这学期，老顾在讲授一门研究生水平的数字几何课程，目前讲到了2016年和丘成桐先生、罗锋教授共同完成的一个几何定理【3】，这个工作给出了经典亚历山大定理（Alexandrov Theorem）的构造性证明，也给出了最优传输理论（Optimal Mass Transportation）的一个几何解释。这几天，机器学习领域的Wasserstein GAN突然变得火热，其中关键的概念可以完全用我们的理论来给出几何解释，这允许我们在一定程度上亲眼“看穿”传统机器学习中的“黑箱”。下面是老顾下周一授课的讲稿。
训练模型
生成对抗网络GAN （
Generative Adversarial Networks
）是一个“自相矛盾”的系统，就是以己之矛克以己之盾，在矛盾中发展，使得矛更加锋利，盾更加强韧。这里的矛被称为是判别器（Descriminator），这里的盾被称为是生成器（Generator）。
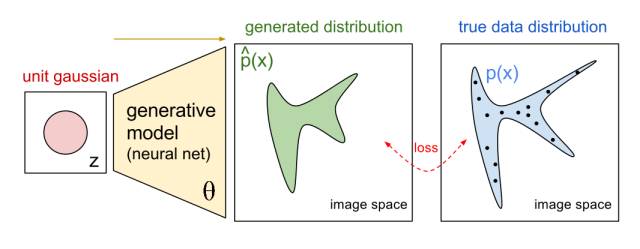
图b. Generative Model.
生成器G一般是将一个随机变量（例如高斯分布，或者均匀分布），通过参数化的概率生成模型（通常是用一个深度神经网来进行参数化），进行概率分布的逆变换采样，从而得到一个生成的概率分布。判别器D也通常采用深度卷积神经网。
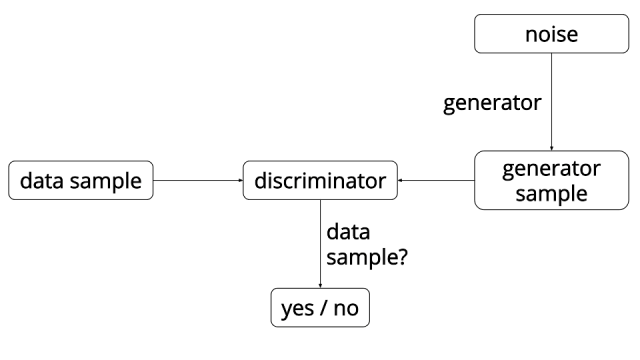
图1. GAN的算法流程图。
矛盾的交锋过程如下：给定真实的数据，其内部的统计规律表示为概率分布
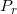，我们的目的就是能够找出
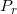。为此，我们制作了一个随机变量生成器G，G能够产生随机变量，其概率分布是
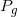，我们希望
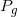尽量接近
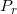。为了区分真实概率分布
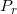和生成概率分布
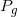，我们又制作了一个判别器D，给定一个样本，D来复制判别这个样本是来自真实数据还是来自伪造数据。Goodfellow给GAN中的判别器设计了如下的损失函数（lost function）， 尽可能将真实样本判为正例，生成样本判为负例：
。
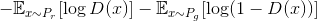第一项不依赖于生成器G, 此式也可以定义GAN中的生成器的损失函数。
在训练中，判别器D和生成器G交替学习，最终达到纳什均衡（零和游戏），判别器无法区分真实样本和生成样本。
优点
GAN具有非常重要的优越性。当真实数据的概率分布不可计算的时候，传统依赖于数据内在解释的生成模型无法直接应用。但是GAN依然可以使用，这是因为GAN引入了内部对抗的训练机制，能够逼近一下难以计算的概率分布。更为重要的，Yann LeCun一直积极倡导GAN，因为GAN为无监督学习提供了一个强有力的算法框架，而无监督学习被广泛认为是通往人工智能重要的一环。
缺点
原始GAN形式具有致命缺陷：判别器越好，生成器的梯度消失越严重。我们固定生成器G来优化判别器D。考察任意一个样本
，
其对判别器损失函数的贡献是
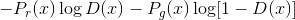
两边对
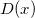求导，得到最优判别器函数
代入生成器损失函数，我们得到所谓的Jensen-Shannon散度（JS）
。
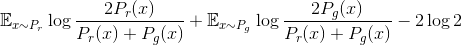在这种情况下（判别器最优），如果
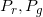的支撑集合（support）交集为零测度，则生成器的损失函数恒为0，梯度消失。
改进
本质上，JS散度给出了概率分布
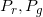之间的差异程度，亦即概率分布间的度量。我们可以用其他的度量来替换JS散度。Wasserstein距离就是一个好的选择，因为即便
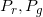的支撑集合（support）交集为零测度，它们之间的Wasserstein距离依然非零。这样，我们就得到了Wasserstein GAN的模式【1】【2】。Wasserstein距离的好处在于即便
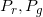两个分布之间没有重叠，Wasserstein距离依然能够度量它们的远近。
为此，我们引入最优传输的几何理论（Optimal Mass Transportation），这个理论可视化了W-GAN的关键概念，例如概率分布，概率生成模型（生成器），Wasserstein距离。更为重要的，这套理论中，所有的概念，原理都是透明的。例如，对于概率生成模型，理论上我们可以用最优传输的框架取代深度神经网络来构造生成器，从而使得黑箱透明。
给定欧氏空间中的一个区域
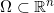，上面定义有两个概率测度
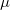和
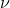，满足
,
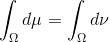我们寻找一个区域到自身的同胚映射（diffeomorphism），
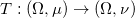, 满足两个条件：保持测度和极小化传输代价。
保持测度
对于一切波莱尔集
,
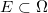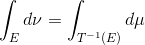
换句话说映射T将概率分布
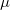映射成了概率分布
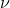，记成
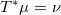。直观上，自映射
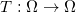，带来体积元的变化，因此改变了概率分布。我们用
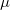和
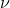来表示概率密度函数，用
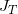来表示映射的雅克比矩阵（Jacobian matrix），那么保持测度的微分方程应该是：
,
，
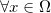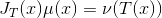这被称为是雅克比方程（Jacobian Equation）。
最优传输映射
自映射
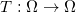的传输代价（Transportation Cost）定义为
。
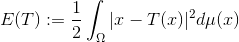在所有保持测度的自映射中，传输代价最小者被称为是最优传输映射（Optimal Mass Transportation Map），亦即：
,
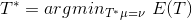最优传输映射的传输代价被称为是概率测度
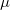和概率测度
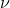之间的Wasserstein距离，记为
。
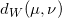在这种情形下，Brenier证明存在一个凸函数
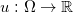，其梯度映射
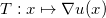
就是唯一的最优传输映射。这个凸函数被称为是Brenier势能函数（Brenier potential）。
由Jacobian方程，我们得到Brenier势满足蒙日-安培方程，梯度映射的雅克比矩阵是Brenier势能函数的海森矩阵（Hessian Matrix），
。
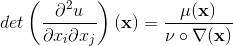蒙日-安培方程解的存在性、唯一性等价于经典的凸几何中的亚历山大定理（Alexandrov Theorem）。
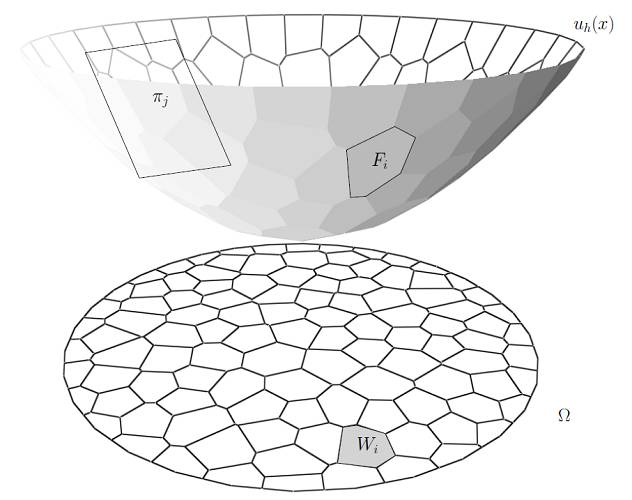
图2. 亚历山大定理。
亚历山大定理
如图2所示，给定平面凸区域
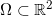，考察一个开放的凸多面体
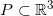，选定一个面
，
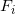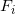的法向量记为
，
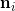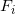的投影和
相交的面积记为
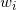，则总投影面积满足
，
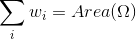凸多面体可以被
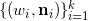确定。亚历山大定理对任意维凸多面体都成立。
后面，我们可以看到，这个凸多面体就是Brenier势能函数，其梯度映射将一个概率分布
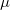映到另外一个概率分布
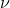，并且这两个概率分布之间的Wasserstein 距离对偶于此凸多面体决定的体积。理论上，这个凸多面体可以作为W-GAN模型中的生成器G。
Wasserstein-GAN模型中，关键的概念包括概率分布（概率测度），概率测度间的最优传输映射（生成器），概率测度间的Wasserstein距离。下面，我们详细解释每个概念所对应的构造方法，和相应的几何意义。
概率分布
GAN模型中有两个至关重要的概率分布（probability measure），一个是真实数据的概率分布
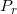，一个是生成数据的概率分布
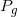。另外，生成器的输入随机变量，满足标准概率分布（高斯、均匀分布）。
图3. 由保角变换（conformal mapping）诱导的圆盘上概率测度。
概率测度可以看成是一种推广的面积（或者体积）。我们可以用几何变换随意构造一个概率测度。如图3所示，我们用三维扫描仪获取一张人脸曲面，那么人脸曲面上的面积就是一个概率测度。我们缩放变换人脸曲面，使得总曲面等于
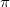。然后，我们用保角变换将人脸曲面映射到平面圆盘。如图3所示，保角变换将人脸曲面上的无穷小圆映到平面上的无穷小圆，但是，小圆的面积发生了变化。每对小圆的面积比率定义了平面圆盘上的概率密度函数。
我们可以将以上的描述严格化。人脸曲面记为
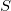，其上具有黎曼度量
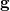。平面圆盘记为
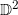，平面坐标为
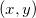，平面的欧氏度量为
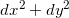。保角映射记为
，
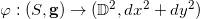则
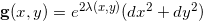，这里面积变换率函数
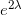给出了概率密度函数。
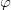诱导了圆盘
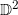上的一个概率测度
。
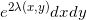图4. 两个概率测度之间的最优传输映射。
最优传输映射
圆盘上本来有均匀分布
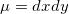，又有保角变换诱导的概率分布
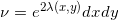，则存在唯一的最优传输映射
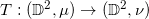。图4显示了这个映射
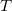，中间帧到右帧的映射就是最优传输映射。我们看到，鼻尖周围的区域被压缩，概率密度提高。
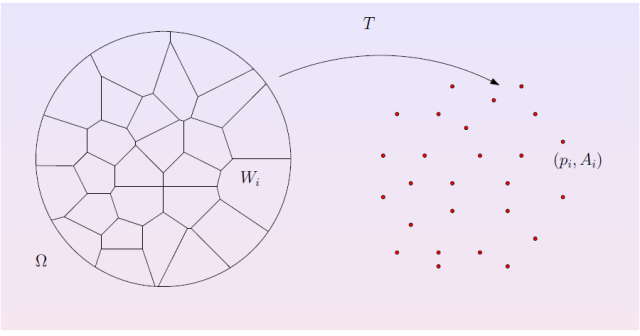
图5. 离散最优传输。
离散最优传输映射
最优传输映射的数值计算非常几何化，因此可以直接被可视化。我们将目标概率测度离散化，表示成一族离散点，
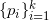；每点被赋予一个狄拉克测度，
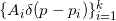，满足
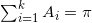。然后，我们求得单位圆盘的一个胞腔分解，
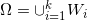，每个胞腔
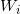映到相应的目标点
，
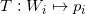。映射保持概率测度，胞腔的面积等于目标测度，
,
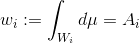同时极小化传输代价，
。
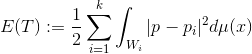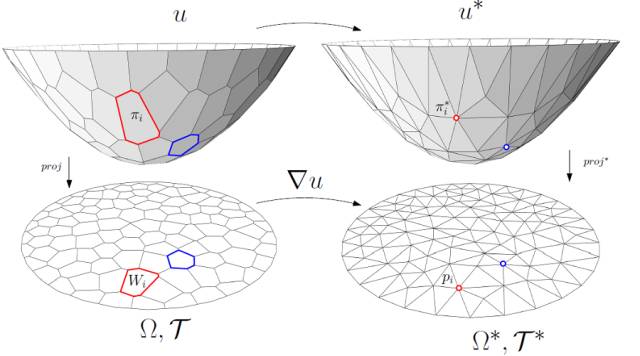
图6. 离散Brenier势能函数，离散最优传输映射。
离散Brenier势能
离散最优传输映射是离散Brenier势能函数的梯度映射。对于每一个目标离散
点
，我们构造一个平面
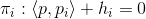，这里平面的截距
是未知变量。这些平面的上包络（upper envelope）构成一个开放的凸多面体，恰为离散Brenier势能函数
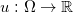的图（Graph）
,
。
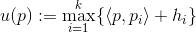图6左侧显示了离散Briener势能函数。凸多面体在平面上的投影构成了平面的胞腔分解，凸多面体的每个面
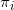被映成了一个胞腔
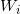；每个面
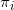的梯度都是
，因此Brenier势能函数的梯度映射就是
。
根据保测度性质，每个胞腔
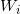的面积应该等于指定面积
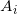。由此，我们调节平面的截距
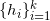以满足这个限制。根据亚历山大定理，这种截距存在，并且本质上唯一。
离散Wasserstein距离
我们和丘成桐先生建立了变分法来求取平面的截距
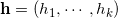。给定截距向量
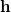，平面族为
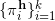，其上包络构成的Briener势能函数为
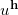, 上包络的投影生成了平面的胞腔分解
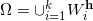, 胞腔的面积记为
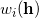。我们定义的能量为，
,
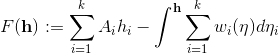这个能量在子空间
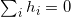上是严格凹的，其唯一的全局最大点就给出了满足保测度条件的截距。这个能量的非线性项，实际上是上包络截出的柱体体积，
，
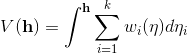图7给出了柱体体积的可视化，柱体体积
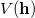是凸函数。
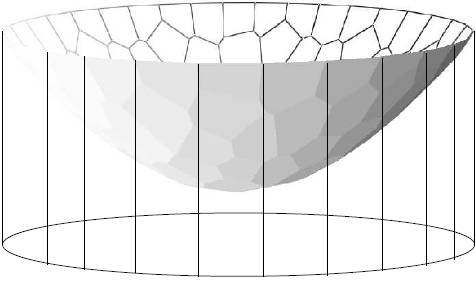
图7. 离散Brenier势能函数的图截出的柱体体积
。
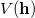体积函数
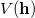和Wasserstein距离之间相差一个勒让德变换（Legendre Transformation）。勒让德变换非常几何化，我们可以将其可视化。给定一个定义在实数轴上的二阶光滑凸函数
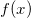，其图
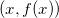是一条凸曲线，这条凸曲线由其所有的切线包络而成。如果，在任意一点
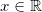，函数的切线的斜率为y，则此切线的截距满足
，
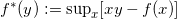