文章
来源：数学中国
在400多年前，人类还没有发明计算机，还只能做加、减、乘、除等简单运算。但是随着科学技术的发展，特别是随着天文学和力学的迅速发展，科学家要面对许多复杂的计算，这就促使他们去寻找简化复杂计算的方法。对数运算与对数表就是在这样的背景下产生的。
人们应该把造出第一张对数表归功于乔伯斯特-别尔基 (JobstBurgi，1552-1632) 和约翰-纳皮尔（John Napier，1550-1617）。他们在制作对数表的过程中所花费的巨大的劳动使人惊讶。法国数学家和天文学家拉普拉斯（Laplace，1749-1827）说：
“
一个人的寿命如果不拿他在世上的时间长短来计算，而是拿他一生中的工作多少来衡量，那么可以说，对数的发明等于延长了人类的寿命。
”
恩格斯曾经将解析几何、对数及微积分并列为十七世纪三个“最重要的数学方法”，而对数的计算又离不开对数表，由此可知对数表的制作成功对科学发展的重要意义。
乔伯斯特-别尔基出生于瑞士，是一个能干的钟表匠和天文仪器技师，他没有受过高等教育，他取得的成就完全是靠他突出的才能与勤奋的工作。他和发现行星运行三大定律的德国著名科学家开普勒（Kepler，1571-1630）一起工作，因为需要进行大量的计算，这就促使他去寻找快速计算的方法。
约翰-纳皮尔是苏格兰人，他也不是职业数学家，但是他受过良好的教育，是一个天文学和数学的爱好者。他完全独立地和别尔基同时开展着类似的研究。他用了20年的时间来制作第一张对数表，在这过程中，他始终怀着一个崇高的目标：减轻未来计算人员的劳动。
下面我们来看看他们是怎样制作对数表的。
由于对数运算有换底公式
所以只要选择一个适当的底，关于这个底制作出对数表，则关于其他底的对数表就很容易制作出来了。那么以什么数作为底最合适呢？
首先，对数表需要满足一个基本条件：表中对数的间隔要充分小，而真数的间隔也要充分小（例如为0.0001）。这样当我们从真数求对数时，很容易在表中找到这个真数的精确值或近似值，从而很快在同一行读出它的对数值；而当我们从对数求真数时，也很容易在表中找到这个对数的精确值或近似值，从而很快在同一行读出它的真数值。
1.
因为我们使用的是10进制，所以先试一下以10作为底是否合适。
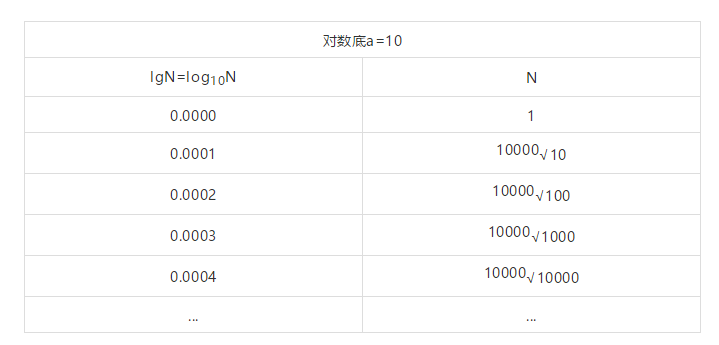
注：上表中
10000
√10表示10的10000次方根。
这个表的左边对数部分的间隔很小，是0.0001，但右边真数部分的计算非常困难，需要对10，100，1000，10000等数求10000次根，这简直是无法计算的。
注：上表中10000√10表示10的10000次方根。
2.
为了避免求上述的开10000次根的运算，我们应该取某个数的10000次幂为底，那么我们先取10
10000
作为底来试一下。
现在这个表右边真数部分的计算不困难了，但这个表不符合我们的要求，虽然对数的间隔比较小（0.0001），但是真数的间隔太大，而且增加太快。
3.
我们把底缩小一点试一下，取2
10000
作为底。
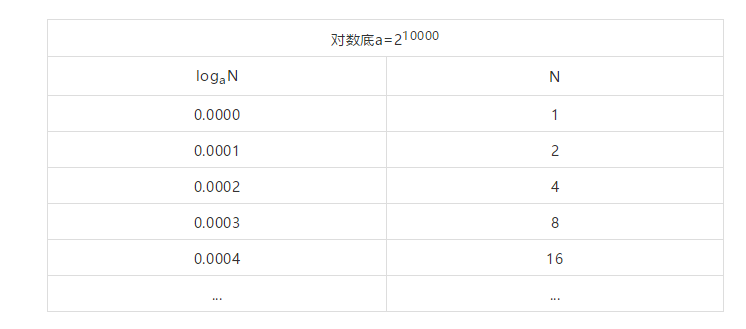
底缩小后，真数这一列间隔也缩小了，但是仍然太大，而且增加也很快。
4.
我们把底再缩小一点试一下，取(1+1/2)10000作为底。
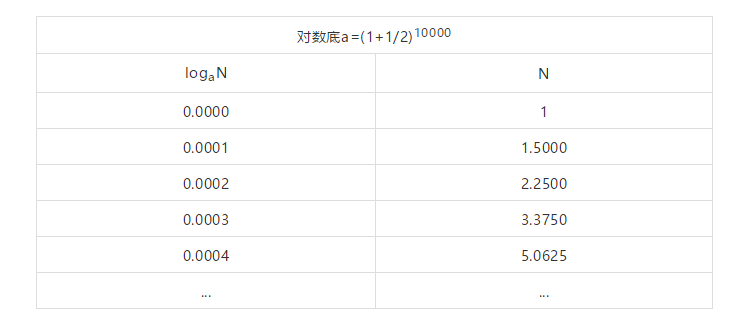
从以上几张表我们可以发现，我们取的底应该是一个指数形式，指数是一个比较大的数，如10000，而底越接近1，真数这一列的间隔就越小。
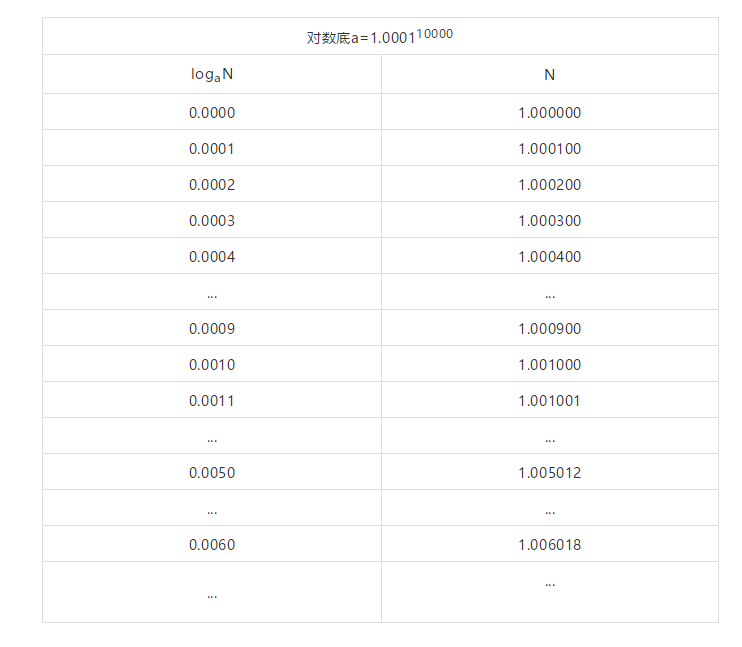
5.
于是自然地想到以1.000110000作为底试一下。
