新朋友请 点上方蓝字“互联网聚焦”免费关注

　不是吹牛，我周围没有人敢和我拼抢红包手速。然而作为一个人品差到极点的人，我经常能在人均几十块的大红包里稳稳地第一个拿下几分钱。

　　这大概就是稳稳的幸福吧……

　　相信许多人都和我一样有一些直觉：

　　比如抢红包貌似后抢比先抢能拿到更多的钱？

　　比如抢红包的金额是和人有关的？

　　目前国内外关于抢红包的理论研究十分匮乏，尽管许多人都认识到了抢红包策略的重要性，但绝大部分人都只停留在了感性的、经验的层面上！

　　我想我有必要对抢红包这件小事开展系统的研究，把它提升到理论的高度！并给出抢红包的最优策略！

　　下面，请大家跟随我的思路，一点点破解抢红包的奥秘。

一、微信红包，先抢后抢究竟公不公平？

直接先亮出答案

不！公！平！

　　看到这里许多读者可能会大吃一惊！那我应该咋办啊！

　　但微信红包先抢后抢的确是有区别的！（我们所说的公平，是指随机、均匀，先抢后抢没有区别。比如抓阄就是一个典型的公平规则，不管先抓后抓，每个人抓到的概率和分布都是一样的。）

　　用一个很简单的抢红包实验就可以证明：

　　比方说有n个人抢一个(n+1)分钱的红包，那结果肯定是某一个人抢到2分钱，剩下的人抢到1分钱。

　　但如果你真的发一个这样的红包你就会发现一个神奇的现象！我称之为“末位红包抽屉原理”(Last red bag drawer principle)

　　末位红包抽屉原理：n个人抢一个(n+1)分钱的红包，必然是前面的人都抢到1分钱，最后一个人抢到那个2分钱！

　　下面由我和我的4个小号为大家具体展示一下实验结果。

　　（1）2个人抢3分钱，是亚清抢到了2分钱。

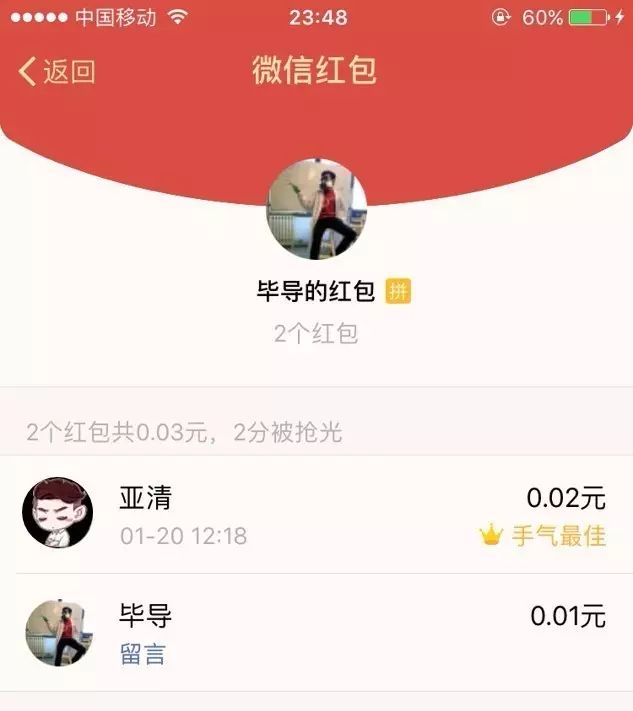
　　（2）3个人抢4分钱，最后一个人抢到2分钱。

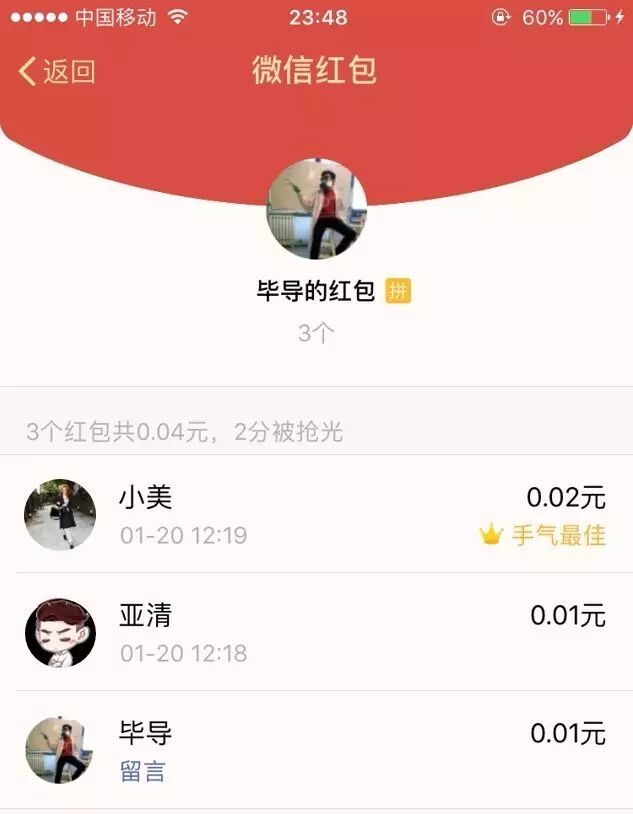
　　（3）4个人、5个人的情况，结论都是一样的！

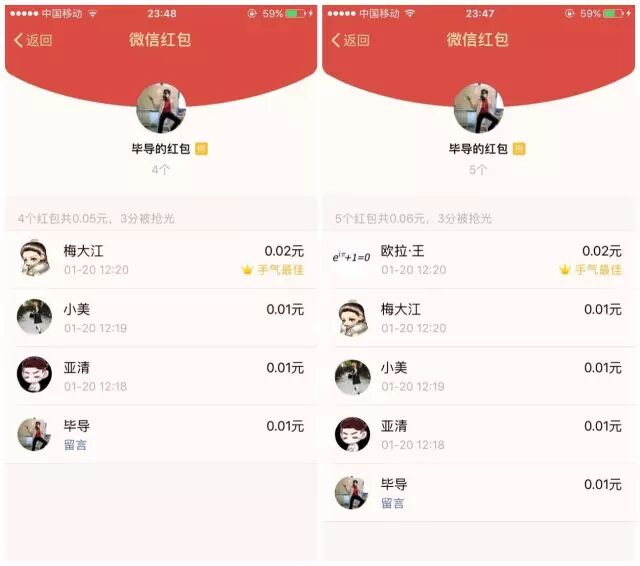
　　过去我们可能本能地认为，微信抢红包无非就是把一个钱随机分成几份，然后随机分给几个抢红包的人。但我的“末位红包抽屉原理”已经充分证明了微信红包先抢和后抢是有很大区别的！否则就不可能永远只有最后一个人能拿2分钱！

二、先抢抢不到大的，后抢才能抢到大金额？

直接先亮出答案：

是！这！样！的！

　　看到这里许多读者可能会大吃两惊！

　　但如果你仔细查查自己抢过的红包就会发现，第一个抢的人永远抢不到很大的数。我称之为“先抢抢不到大红包原理”(First rob rob no big red bag principle)

　　下面我和我的4个小号为大家带来一组抢红包实验！

　　【实验内容】我发50块的红包，给5个人抢。红包发了210个，记录每次第1个人抢到的金额。（抢的顺序是经过打乱随机的，以排除人品等干扰因素。）

　　结果表明，第一个抢的人抢到的红包金额分布范围是这样的：

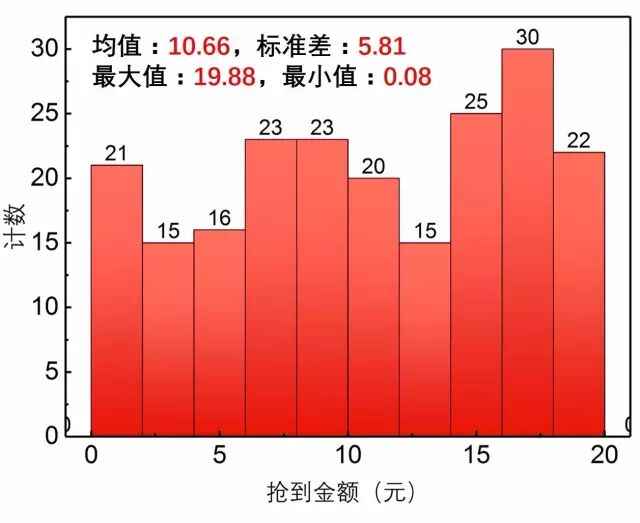
　　图2. 第一个人抢到的微信红包金额频数分布直方图

　　发现这其中的诡异之处了吗？

　　5个人抢50块红包抢了210次，第一个人竟然永远抢不到20块以上的红包！最高只抢到过19.88元！

　　也就是说，真正的大红包都只会在后面出现，像这样：

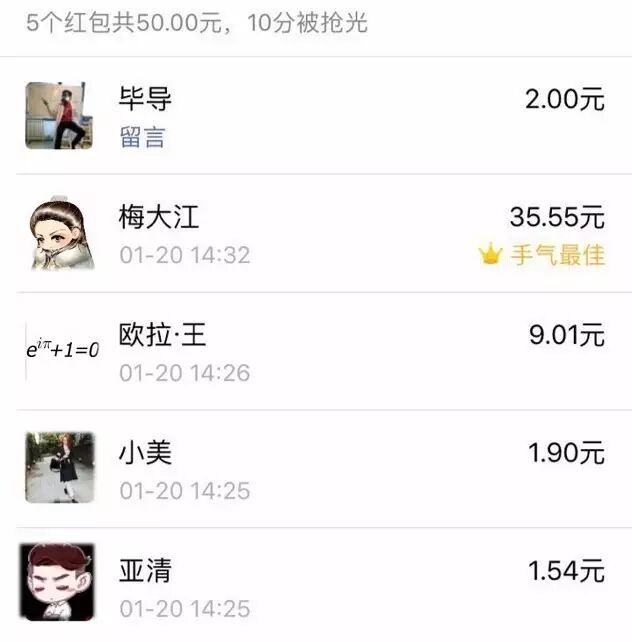
　　为了进一步研究这其中的规律，我准备了大量资金，发个痛快！

　　【实验内容】定义5个人的标准顺序：毕导-亚清-小美-欧拉·王-梅大江。轮换他们的顺序，在每一种顺序下发50块红包，抢30次，共150次。记录每次5个人抢的红包金额，得到750个原始数据。（如下图所示）

　　最终得到的五个人抢到红包的金额范围分布是这样的：

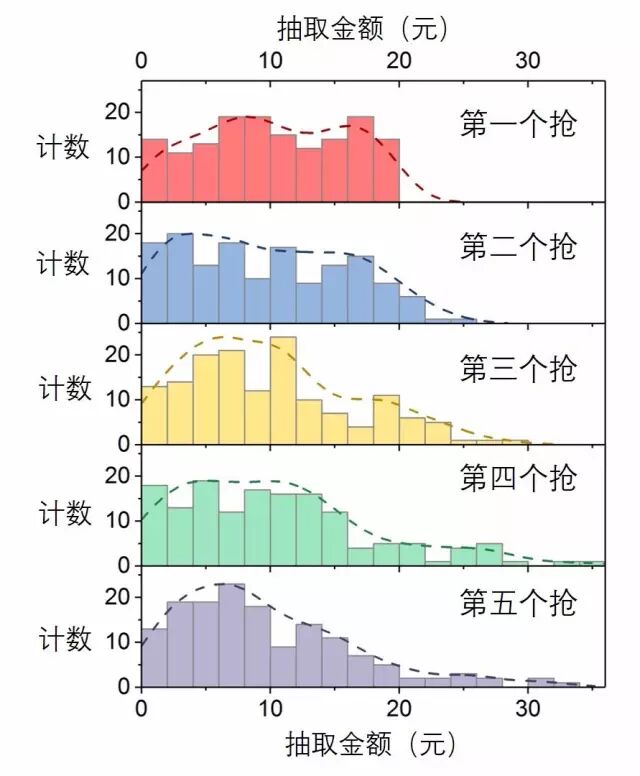
　　图3. 不同抢红包顺序抢到的金额频数分布直方图

　　这张图已经可以告诉我们许多规律了：

　　可怕！早在2014年我就已经开始暗自用打地鼠游戏练习抢红包，最终习得一身技艺，指如疾风，势如闪电，可以扫平所有群的所有红包，江湖人称“红包霹雳手”！

　　然而现在看来，“先抢抢不到大红包原理”已经注定了，正是我超凡的手速让我输在了起跑线上……

　　我必须要继续探究出一套最佳的抢红包策略！

三、抢红包和人品有关吗？

　　在进一步实验之前，我觉得首先得排除一个因素的干扰……

　　世间万物都有它运行的法则！

　　理论上讲，你出敬业福的概率和我是一样的，但就是有人抽得到有人抽不到。

　　生活中的种种不公平让我们不得不思考：除了概率之外，还有一种更重要的东西在左右着我们的客观世界——人品！

　　5个人抢的150个50元红包的结果是这样的：

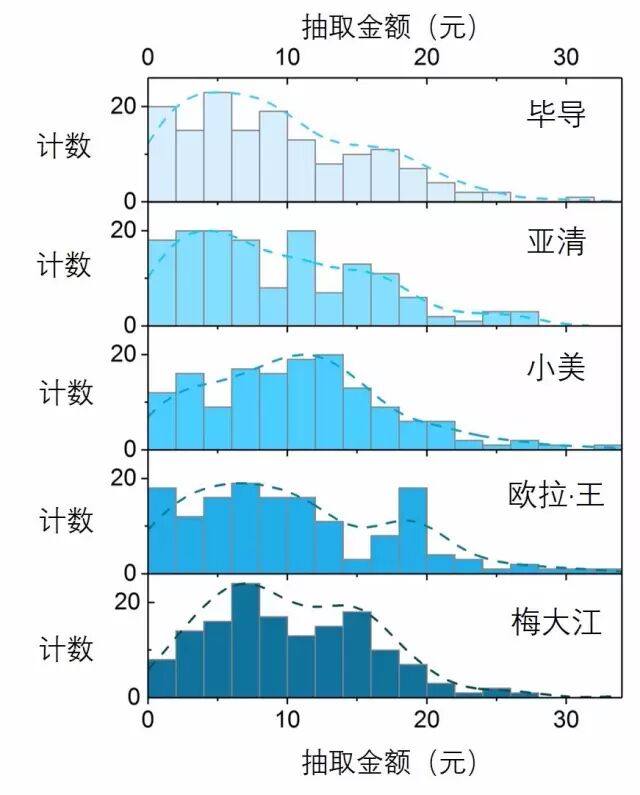
　　图4. 五个人抢到的金额频数分布直方图

　　呃……至少五个人都能抽到大红包……脸还不算太黑……那么究竟谁最厉害呢？请看下面的散点图以及表格数据。

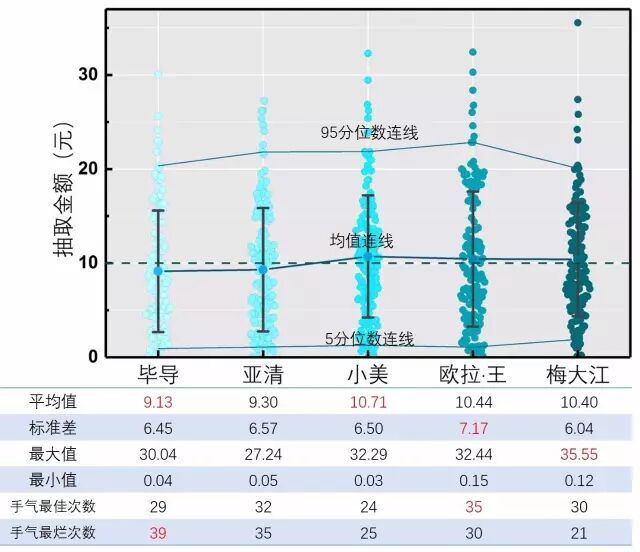
　　图5. 五个人抢到的金额

　　5个人抢50块，平均每人10块钱。

　　从图上可以看出，5个人的平均值都是在10块钱附近，标准差也都在6~7之间。

　　但是细细看看统计数据还是有明显差异的……

　　我的平均值只有9块1！小美有10块7！这差距也太大了吧！

　　我的手气佳次数也很低！而手气最烂次数排名第一！

　　综合看来，小美的人品最好，欧拉·王其次但是发挥不稳定，下来是梅大江、亚清，人品最差的就是我……

　　--“所以微信抢红包这事和人究竟有没有关系啊？”

　　--“人品这种事情，如果能用理论算的话还叫人品吗？”

四、抢红包最优策略是什么！

　　人品这种虚无飘渺的因素还是撇开不谈了，抢红包的时候我们唯一能控制的就是先抢还是后抢！另外我记得之前微信群里经常有抢红包的游戏，规则很简单，就是抢到“手气最佳”的人要继续发红包。

　　所以接下来我们的研究任务是！

　　依然采取前面的那组实验数据，在五种抢红包顺序下的原始数据是这样的

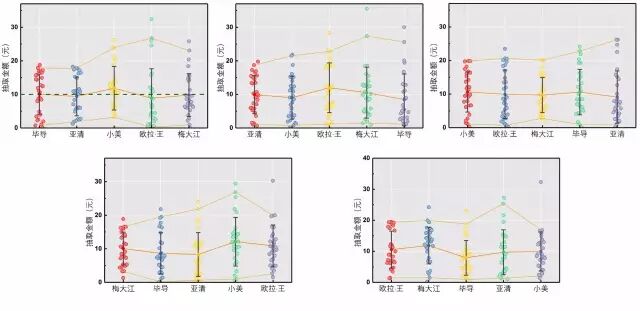
　　图6. 五种顺序下抢到的金额

　　直观上看大家平均都在10块上下波动

　　下面我们忽略人的因素，把五张图的数据汇总到一张图上！

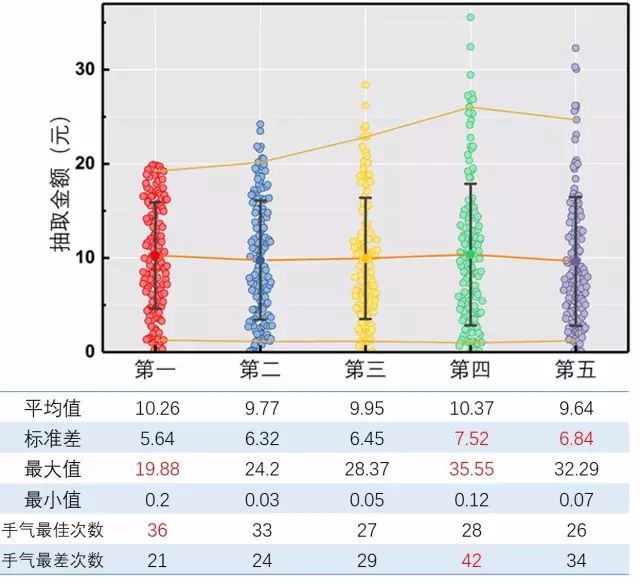
　　图7. 五种顺序下抢到的金额汇总

所以抢红包的最优策略如下：

　　看到这里可能有人会质疑，你这不就只做了150个红包实验，样本量太小，得出来的结果可能根本不具备普遍规律啊！

　　我的探究当然不会就此停止！

五、微信究竟怎么设计的抢红包？

　　按照正常的套路，抢红包最简单的办法不就是把红包的总钱数随机分给几个人么……但是微信偏不这样，就是一定要让第一个人抽到的钱只能在0.01元到20元之间。

　　对于5个人抢50块红包而言，20元是个什么数？

　　在一篇《微信红包的架构设计简介》的文章中提到这可能是“平均值的2倍”(也就是说，每个能抢到的钱最多是当前剩余金额的平均值的2倍)

　　虽然不明白微信为什么要搞这套规则，但是我们不妨拿数据检验一下这个规则对不对！

　　（1）检验第一个人抢到的金额是否服从均匀分布

　　简化：抢红包问题本身是(￥0.01,￥0.02,…)的离散分布，在此为检验均匀分布，将其作为连续分布近似处理。

　　首先对每个人作为首抢时的数据分析，进行Kolmogorov-Smirnov检验，利用累积分布函数检验第一个人抽到的金额是否服从均匀分布。假设检验均通过，得到类似“毕导第一个抢时，毕导抢到的金额确定是均匀分布”的结论。

　　（2）检验是否有人品因素的干扰

　　看五人分别作为首抢时是否有个人因素导致抢到金额有分布上的差异，进行Anderson-Darling k-样本检验，发现其实没有。所以抢红包次数足够多的前提下，不存在脸帝光环。

　　（3）抢到的金额是多少到多少的均匀分布？

　　最小值肯定是0了，因为实际中已经知道有人不管红包金额多大都只能抢到1分钱。

　　根据统计推断的点估计理论中的极大似然估计知道，参数的极大似然估计是最大值。我们的210组抢红包数据中，第一个人最大就抢到过19.88元。

　　但是极大似然估计往往低估了，采用贝叶斯估计的方法。先验分布选共轭的帕累托分布，后验均值是mN/(N-1)=210/(210-1)*19.88=19.975。

　　基本可以在统计学意义上断定，均匀分布的右端点是20。

　　（4）后面抢的人也服从0.01~剩余均值2倍的均匀分布吗？

　　根据第一个人的均匀分布可以递推出第二个人的分布密度函数，进一步用类似方法检验第二个人抢的金额是否符合这个密度函数。检验同样通过，第二个人的金额服从0.01~剩余均值2倍的均匀分布。当然从算法的简洁性上来说，微信也不太可能给第一个抢和后抢设置不同的算法规则。因此我们有一定的理由相信微信红包是按这个规则设计的。

　　至此基本可以给出微信设计的抢红包规则了：

　　每个人能抢到的金额服从0.01到2倍剩余均值之间的均匀分布。 

　　我们5个人抢50块：

　　第一个人最多能抢到2*50/5=20元，比如他抢了5元，此时剩下45元。

　　第二个人最多能抢到2*45/4=22.5元，比如他抢了12元，此时剩下33元。

　　第三个人最多能抢到2*33/3=22元，比如他抢了17元，此时剩下16元。

　　第四个人最多能抢到2*16/2=16元，他和第五个人分这16元。

　　下面要考虑的问题是：这种规则产生的红包，是否会导致先抢后抢均值相等，而后抢的方差更大？

　　将问题抽象为n个人抢一个S元的红包

　　证毕，在微信红包的“0.01~2倍剩余均值均匀分布”算法下，先抢后抢的均值相同，越往后抢方差越大。最后两个人同分布。

六、没事闲的

　　现在既然我们已经知道了微信红包的算法原理……那就可以编程给自己发红包看规律了……

　　出于礼貌，我用matlab给自己发了五万个红包。五个人抢红包金额分布图是这样的（纵坐标太大隐去了……）

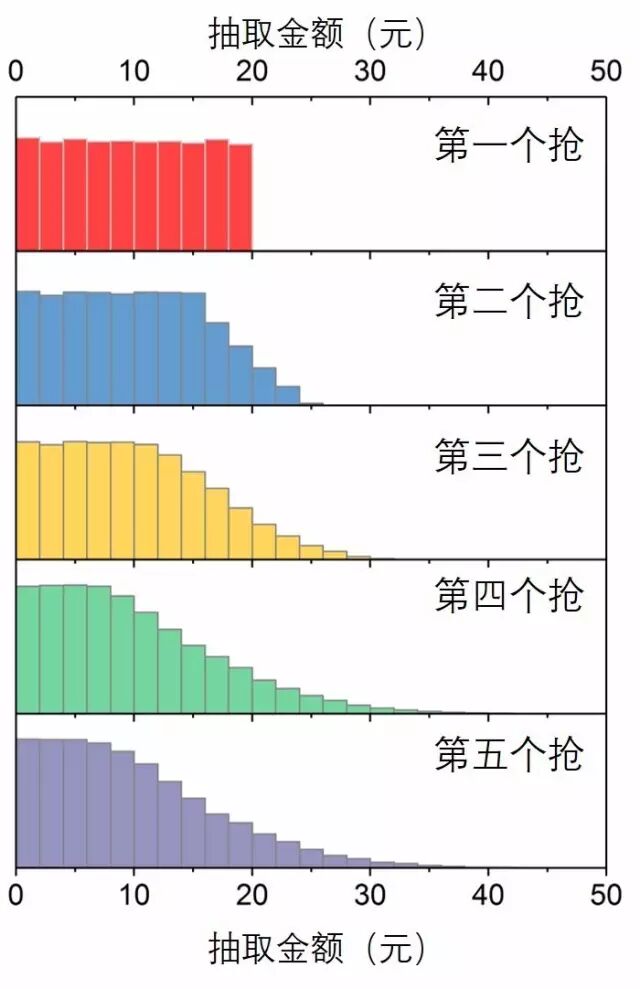
　　图8. 不同先后顺序抢到的金额分布图（五万次模拟）

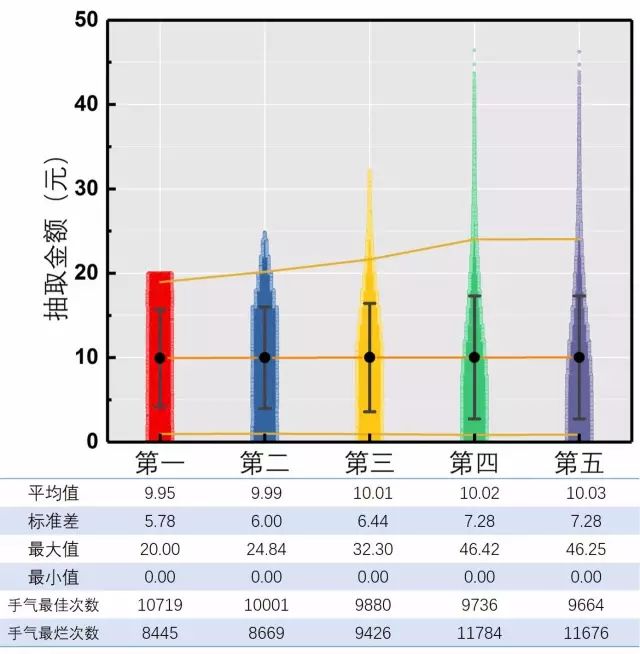
　　图9. 不同先后顺序抢到的金额汇总（五万次模拟）

　　结果一切尽在掌握之中！均值相同，标准差变大，第一个人有最多的“手气最佳”！

　　由于最近真的有人拉我玩“手气最佳发红包”的游戏，吓得我赶紧给自己发了一千万个红包研究理论规律。

　　毕竟这个游戏里只抢不发是最好滴，一抽到手气最佳之前抢的钱都白费了。

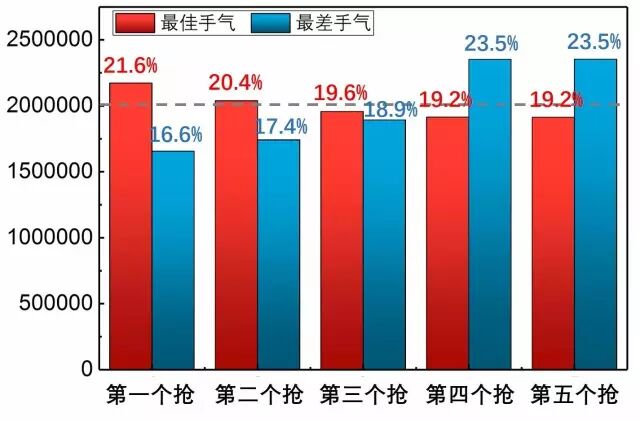
图10. 不同先后顺序下抢到的手气最佳、最差（一千万次模拟）

　　看来先后顺序对抽到“手气最佳”是有决定性影响的！

　　5个人抢红包的时候，越先抽，抽到“手气最佳”的概率越大！第1个人抢到手气最佳的概率是21.6%，而最后俩人的概率只有19.2%！相反，第1个人抢到手气最差的概率是16.6%，最后俩人的概率高达23.5%！

　　不过只有5个人抢的时候有这个规律。

　　当参与抢红包的人数变化时，“手气最佳”的概率随着先抢后抢顺序变化的规律也是不一样的。

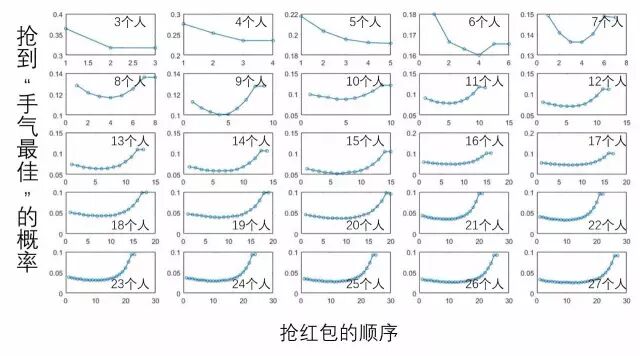
　　所以一帮人玩“手气最佳发红包”的游戏时

七、结论

微信抢红包的规律

　　规则：每个人能抢到的金额服从“0.01到2倍剩余均值”之间的随机分布。 

　　均值：不论先抢后抢，均值都一样

　　标准差：后抢的标准差更大，可能抢到超级大红包，也可能抢到超级小红包

　　最大最小值：第一个抢抢不到大红包，后抢才可能抢到超级大红包

　　手气最佳：和红包的个数是有关的，见第六部分

抢红包的最优策略是

　　风险偏好：如果你想要稳稳当当地抢，就先抢；如果你喜欢抢到超级大红包，就后抢。

　　“手气最佳发红包”游戏：发的红包数少就后抢，红包多就中间抢，很多就先抢！

　　经过这么漫长的系统研究我终于得出了最优策略！

　　我很兴奋地去和他们玩“手气最佳发红包”游戏了！

　　结果！！！

【写作不易，记得转发】

了解更多重大新闻，您可以关注我们的微信号

头条新闻，重大事件，每天为你报道

互联网聚焦

十年前引领中国经济的是楼市与金融

未来十年引领中国经济的绝对是互联网

拇指长按下方图片

点“识别图中二维码”关注我们