在前两篇文章中,我们介绍了三角化恢复深度信息,并对三角化过程中的误差进行了分析和讨论。
今天,我们就进入我们这个系列的正题:深度滤波器的原理及实现。
一提到深度滤波器,大家肯定首先会觉得深不可测,听名字就觉得高大上。其实,有了前面的预备知识,不难理解今天要讲解的深度滤波器的原理。
我们今天给大家介绍的是比较简单的高斯分布假设下的深度滤波器。
高斯分布是自然界中最常见的一种分布形式,并且也符合绝大部分的自然情况。简单起见,我们先假设三角化后恢复的深度值符合高斯分布。对于像素点的深度值d,满足:
P(d) = N(μ,σ2)
每当新的数据过来,我们就要利用新的观测数据更新原有的深度d的分布。
这里的数据融合的方式与经典的Kalman滤波方式大同小异。
这里,我们利用观测方程进行信息融合。
假设新计算出来的深度数据的分布为:
P(dobs) = N(μobs,σobs2)
我们将新计算出来的深度数据乘在原来的分布上,进行信息融合的更新:
我们知道,利用两个高斯分布的乘积的分布公式,可以得到融合后的高斯分布:
P(dfuse) = N(μfuse, σfuse2)
其中,
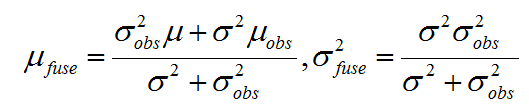
那么问题来了,这里的μobs,σobs2该如何才能得到呢?
这里的μobs实际上就是每次我们新三角化出来的深度值,而对于σobs2,如果你还对上一篇文章有印象的话,就会记得我们推导了一系列公式所得到的那个 δp(不确定度σobs),如果你忘记了,可以回去上一篇文章再复习一下。
那么原始的分布μ,σ2该如何得到呢?
这个很简单,第一次三角化出来的μ,σ2就可以作为初始值,然后每次新三角化出一个三维点,就去更新深度值的分布。
至此,我们似乎得到了一个不错的结果:既简单又优美的公式。
实际上还会存在什么问题呢?
(1)实际的深度值分布是否真的符合高斯分布?
(2)如果我们中间过程有一次三角化的过程求错了,并且还进行了信息融合,会有什么后果?
(3)我们如何避免第二个问题中所提出的情况?
这些问题留给读者去思考,也欢迎在下方给我留言,一起探讨这些问题的解决方案。
下篇文章我将会带着大家一起分析一下高博的单目稠密重建的代码,有了前三篇文章的理论铺垫,相信你读起来下一篇文章中的代码会如鱼得水。
我们下一期再见!
参考文献:
《视觉SLAM十四讲:从理论到实践》,电子工业出版社,2017,高翔等著。
【版权声明】泡泡机器人SLAM的所有文章全部由泡泡机器人的成员花费大量心血制作而成的原创内容,希望大家珍惜我们的劳动成果,转载请务必注明出自【泡泡机器人SLAM】微信公众号,否则侵权必究!同时,我们也欢迎各位转载到自己的朋友圈,让更多的人能进入到SLAM这个领域中,让我们共同为推进中国的SLAM事业而努力!
【注】商业转载请联系刘富强([email protected])进行授权。普通个人转载,请保留版权声明,并且在文章下方放上“泡泡机器人SLAM”微信公众账号的二维码即可。





