
日本理化学研究所先进智能研究中心主任杉山将
记者 | JayZhang
7 月 22 - 23 日,在中国科学技术协会、中国科学院的指导下,由中国人工智能学会、阿里巴巴集团 & 蚂蚁金服主办,CSDN、中国科学院自动化研究所承办的 2017 中国人工智能大会(CCAI 2017)在杭州国际会议中心盛大召开。
在本次大会上,日本人工智能和机器学习领域新一代的代表性人物——日本理化学研究所先进智能研究中心主任Masashi Sugiyama(中文名:杉山将)为参会者带来了《弱监督机器学习的研究进展》的演讲。杉山将在机器学习领域发表过很多重要的理论,是这个领域最知名的学者之一,出版了机器学习相关书籍《图说机器学习》(中文版)。
以下内容根据杉山将本次主题演讲整理,略有删减:
大家早上好,我叫杉山将,非常高兴能够参加今天的大会,也很高兴和这么多中国的研究人员见面,我也特别喜欢杭州的文化和当地的美食。
在过去的4-5年中,AI在日本发展地非常快,这也让我能有机会出相关的教科书,其中有一本翻译成了中文——《图说机器学习》。其实我看得懂中文,所以我觉得今天演讲的中文标题的翻译是很准确的。
下面我所要讲的东西和今天大会的主题非常契合。

昨天漆远谈到了金融领域的机器学习,从大数据的角度来看,它是机器学习很重要的研究领域,并且目前还是非常的成功,我也一直对基于大数据来做机器学习这件事情非常感兴趣。然而,现在对于很多的应用领域而言是无法获取大规模的标注数据的,比如医药、制造业、防灾等领域。当数据量不够时,我们需要相应的机器学习方法来应对。
今天我会讲一些关于小数据的研究进展,我的演讲和其他的演讲者相比会更没有那么的技术性,希望大家可以了解一下小数据分类的研究状况,其中还是有一些让人欣喜的研究进展的。
监督学习、非监督学习和半监督学习概述
回到我们所讨论的话题,首先还是要去关注一个最简单的问题,就是二元分类的问题。
我们会有一些训练数据(如下图),其中蓝色圈点代表正例,而红色叉点代表负例。这样的二分类问题,其实已经被研究很多年了,由于我们已经有了大量的标注数据,所以能够得到非常好的分类结果,我们都知道现在最优的分类结果是这样的。

然而,想要获取大量的标注数据是非常耗时耗力的,我们希望也能够对无标注数据进行分类,这就是无监督分类的由来。
其实无监督分类和聚类是一样的,比如下面这张图中的数据点聚成了两簇,每一个簇代表一个类别,这样才是非常好的分类结果。然而很遗憾现在我们这个假设(即聚类的结果表示一个类别)并未得到相应的验证,所以从这个层面上来看,还没有非常合理的办法来做无监督分类。

我非常喜欢11年前提出另一种方法的论文:由于我们有大量的无标注数据和少量的标注数据,那么基于少量的标注数据就能在一定程度上找到边界,然后结合所找到的边界和大量无标注数据的聚类结果,从而找出更多的边界。这就是半监督分类。
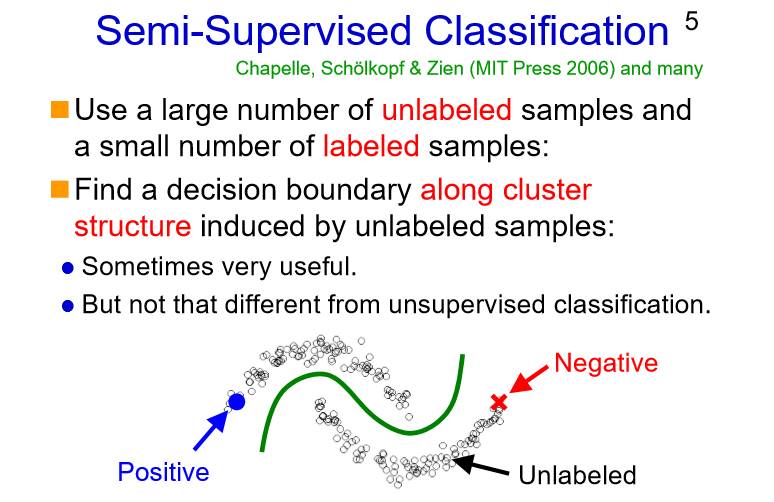
然而,半监督分类和无监督分类面临同样的问题,也就是簇要能够跟类别对应起来。如果一个簇总能对应着一个类别,这样就完美了。但事实并非如此,这就是我们今天所要讨论的内容。
接下来我先总结一下前面说过的内容。
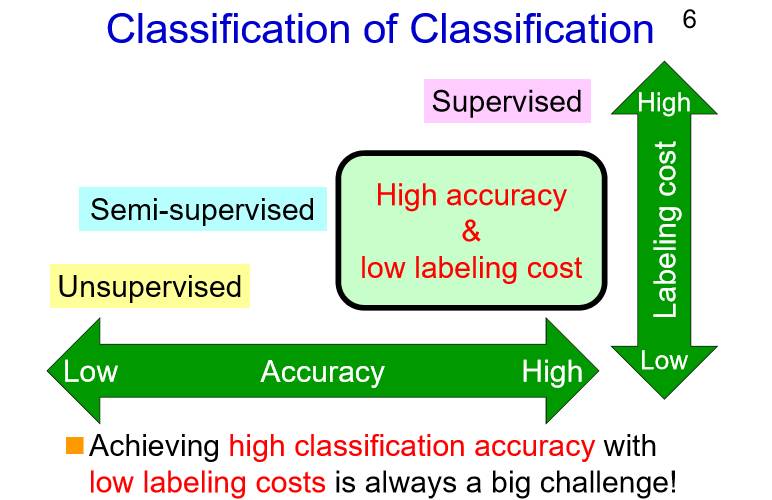
对于不同类型的分类方法,标注的成本有高有低,所取得的分类准确率也有高有低。对于监督分类,能够取得很高的分类准确率但同时标注的成本非常高;而对于半监督和非监督分类,标注的成本都比较低(甚至没有),但取得的分类准确率并不高。
如何让左下角的这两种方法(即半监督和非监督分类)能够取得较高的分类准确率,同时保持比较低的标注成本?
这是我们所面临和需要解决的难题。
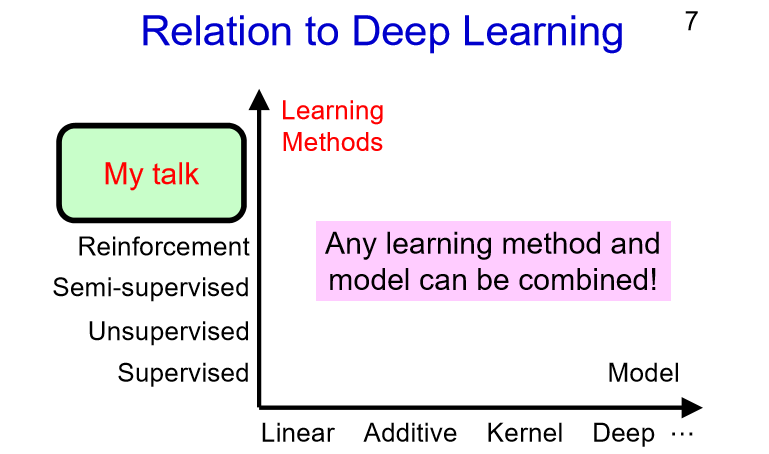
现在深度学习技术非常热门,但我今天讲的东西不是深度学习,这并不是说要忽视深度学习,其实这个话题跟深度学习也是有关系的。
模型方面,从简单到复杂,我们有线性模型、增量模型、基于核函数的模型和深度学习模型等;机器学习方法方面,有监督学习、无监督学习、半监督学习和增强学习等。
任意的学习方法和模型都是可以相结合的,不过我今天要讲的东西是关于学习方法的,它可以使用任何的模型,包括深度学习模型。当然我更倾向于使用线性模型,因为这更简单,如果你想使用更加复杂的模型也是完全可以的。
弱监督学习的研究进展
下面是今天演讲的议程,接下来会给大家介绍四种不同的分类方法,后面如果有机会我会介绍一下理化学研究所AIP研究中心。

UU数据分类
首先看一下UU (Unlabeled, Unlabeled) 分类,U代表的无标注的数据(Unlabeled data)。
那么我们是怎样对无标注的数据进行分类的呢?假设我们有两个未标注的数据集,它们唯一的不同在于类先验(class-priors,即所属的类别)的不同。它们的函数分布如图中的左右下角,数量上各占50%左右,其实我们并不需要知道具体的比例。基于这种假设,我们需要训练一个分类器,而基于无标注数据的训练是极具挑战的。

那么怎么训练分类器呢?
首先来看一下类先验的区别是什么,在正类和负类之间,我们只看p(x)和p’(x)之间的差异,这就是我们划分正负类的标准。
假设通过某些技术方法,我们能够获取这些数据的正负类分布的先验信息,正负类的分布比例是对等的,也就是说一半数据是正类,一半是负类。x代表非标注的数据,C是一个常数,由于没有相应的标注数据,所以我们对C的值难以有个合理的估计。尽管如果C没有具体的值,我们不知道哪一侧是正类,哪一侧是负类,但这并不要紧,因为类别之间的差异性往往很明显,最终表现在符号为正或负,所以我们有时可以将常数C忽略掉。我们只看最终符号的正负,这样可以让我们得到最优的分类结果。

接下来的做法都是很直观的。因为我们要处理的是一些未标注数据,第一种方法是做核密度的估计,我们对两类数据点对应的p(x)和p’(x)进行估计,从而计算它们之间的差值,这样能够很自然地解决分类问题。然而,遗憾的是这种方法虽然简单,但有可能对p(x)-p’(x)的差值产生了低估,这是因为对p(x)和p’(x)的估计函数过于平滑所导致的。
第二种方法是直接对密度的差值进行估计,利用Kim等人所提出的模型,尽可能把密度差异的估计偏差达到最小,这种方法用一个线性的模型就能够得到相应的解决方案。
第三种方法是对密度差的第一项进行直接的估计,这是最为直接的方法。对于我们这个问题来说,第三种方法遵循了Vapnik原则。我们要解决的问题不能太过泛化,在这个场景中,我们想要估计密度的差值,这将涉及到非凸优化方面的问题(例如可使用CCCP方法来解)。

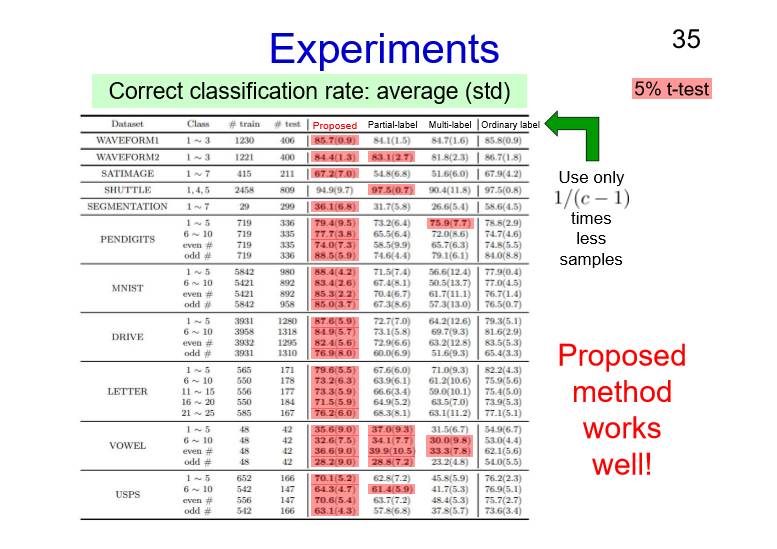
下面是我们做的一些实验结果,比较的指标是误分类率的类均值。
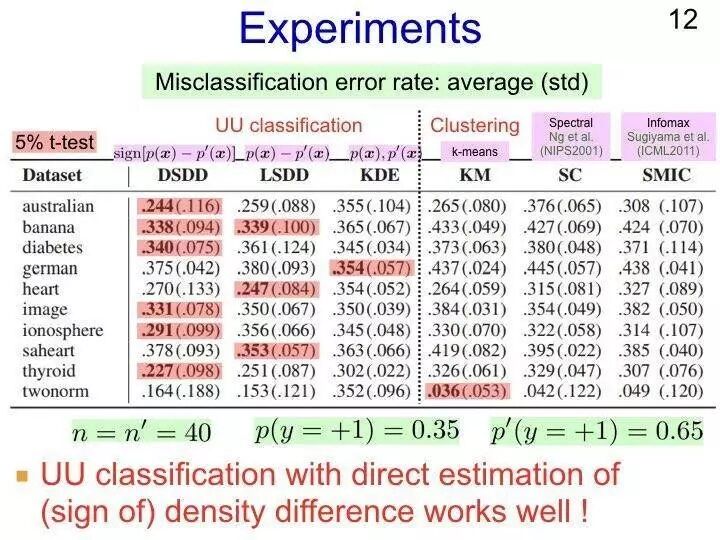
表格的左侧一栏是表示不同的数据集,对比的方法中有聚类的方法,可以看出聚类的方法并不是很有用。表格中间的是一些普通方法,其中第二种是估计p(x)-p’(x)的差值,可以看出越靠近左侧的方法取得的效果越好,这是因为对应解决问题的方式更加直接,因此直接的估计密度差值或者是密度差值的符号函数的值会更加有效。
在实际的应用中,我们通常选择左侧的两种方法。
PU数据分类
下一个话题要谈的是如何处理PU (Positive, Unlabeled)的数据,也就是只有正例数据和未标注的数据。
我们有两类数据样本,一种是属于正类的,另外一类是未标注的。当然未标注的数据里包含了正类和负类两种数据,但是我们并不知道其中哪些是正类,哪些是负类。对应这种数据类型的一个例子是,比如有一些你点击和未点击的网站,对于那些未点击的网站中,你既有未来可能会点击的,也会有你不会点击的(或者有想点击的,但可能由于忙而没有真正点击的),对这些网站点击数据,我们可以应用PU的分类方法。
另外,我相信在社交媒体上面也会有这样的分类场景,判断一个用户是不是你的好友。对于已经认识的朋友,朋友之间有着很好的联系,所以我们能够得到相应的数据样本;然而,对于非朋友关系的用户们,我们并不知道他们相互讨厌对方所以没有成为朋友,还是如果有机会是能够成为朋友的,所以他们之间没有链接并不代表它就是负类的(不能成为朋友)。

在这个PU分类中,我们还需要获取一个PN的分类器,因为尽管我们有了正例数据和未标注数据(对应图中的蓝色和黑色的符号数据),我们还是要知道未标注数据(黑色的符号数据)中哪些是负的哪些是正的,这里也将涉及到很多的公式,我们接下来看一下分类器的风险函数。

我们用到了损失函数,用了l表示; y是用f(x)表示;我们用R(f)表示风险函数,代表数据分类的风险,可以看到风险函数包括正类数据的分类风险以及负类数据的分类风险。在今天的演讲当中我们为了把它讲的简单,这里实际是要通过这些数据来进行估计的。
我们现在有正类数据和负类数据的分类风险,已经分成两类。因为我们在PU分类任务中缺少对负类数据的标注,因而我们不能对负类数据的分类风险进行直接的估计,这也是我们技术上所面临的挑战。然而,这个问题可以很简单的来解决,由于未标注数据是由正类数据和负类数据组成的,所以我们可以从PU数据中来对负类数据的分类风险进行一个预估。
具体的公式转换如下图所示,它背后的理论是正负数据分类风险满足一定的边界条件,具体的细节在这里就不细说了。这是最优的方法,我们可以通过PU的学习,从PU的数据中得出PN的信息。

在左边PU的边界可以比PN的边界要小,我们一开始是用PU的结果而没有PN的,这是我们的起点。但如果满足了这个条件,PU数据的学习要比PN数据的学习更好,但前提是我们要有大量PU数据;因为如果说有大量的PU的数据的话,我们左侧边界值就会变的小一些。所以说,PU的学习有时候可以比PN更好一些,这让我们研究出下一种方法,我后面会给大家看另外一种方法。

我们会发现,尽管PU方法已经能够取得很好的结果,但是还是存在一些问题。
我们再来看一下之前的PN的风险函数公式,就是基于P数据和N数据的风险对U数据的分类风险进行估计。根据这个定义,N数据的风险是非负类的,但是它是PU的样本,在现实当中我们要对样本进行估计。所以说PU可能是会为负的,因为这个是会有一个负号,通常是应该是负号的,但有可能这个差会是负的,特别是对于可扩展性较高的模型来说,比如说像深度网络是会出现这个情况。

我们看到,对于非负类的PU分类,先从虚线的蓝线开始看起,是PN的测试数据上的误差结果(蓝色的实线),这表示模型是收敛的。
再看一下红色的虚线,是PN的训练数据上的误差结果,在到某个点的时候会变成负,这表示模型的训练已经出现了过拟合。因为当在训练数据的误差值变成负了之后,PU测试数据上的误差值开始增长了。一个简单的解决过拟合的方法是,限制这些误差值为非负。
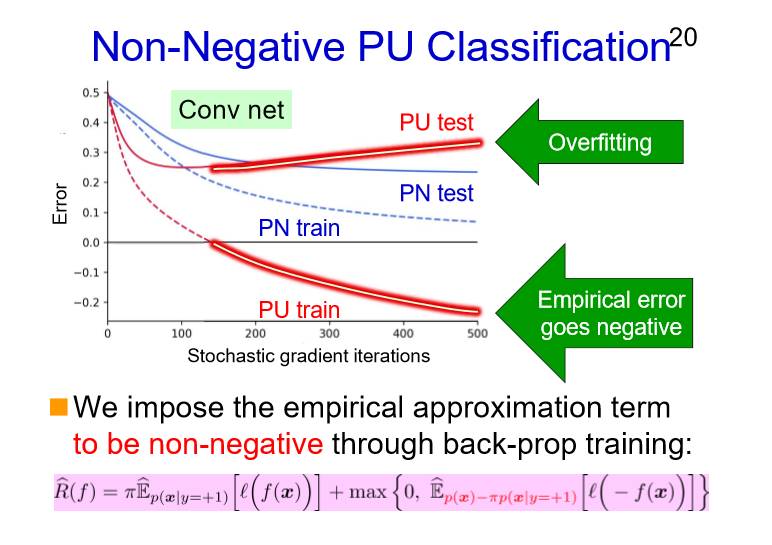
这样做的话,就可以让我们的数值维持非负性。
但这里的一个问题是在于,这样的模型对于现在的风险预估而言效果还是可以的,但是并没有解决全部的问题。
首先我们先看一下风险的偏差值还是有一致性的,如果你输入的样本太多,它会产生真正的风险,而且它的偏差的下降是指数级的。从应用的角度,我们可以去忽略R(f)的偏执项,这样均方误差其实并不比原来的那个均方误差要大,而R(f)的值也会变得更加的可靠。

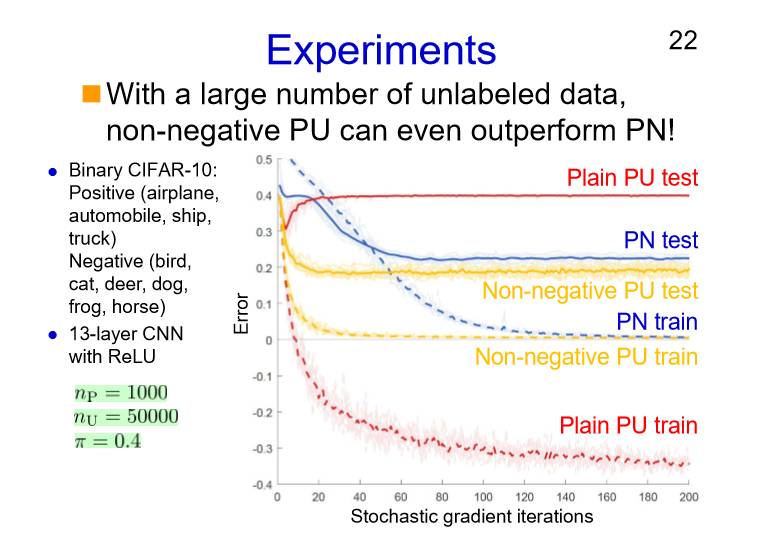
最后我们看一下实验结果:在线性模型当中,可以在测试数据上收敛,当然现在这样的方法只能用于线性模型。虽然没有办法获得一个更通用的经验,但是我们可以能够对于这样的偏差预估性的方法来进行改良,兴许将来有更好的应用。所以,我们在CIFAR10当中创建了很多的正类的数据,蓝色线代表PN测试。在这里可以看到,如果np等于1000错误率下降非常快;如果说是对于非负的测试数据,比如说就是这条黄色线和蓝色虚线的话,它的错误率下降就并不是那么的明显;如果说我们使用一些ReLU方法,PU做的比PN要好的多。
接下来做一个简单的总结:PU数据分类是怎么做的?我们做的非常简单,就是把P和U数据,就是黑色跟蓝色符号数据进行分开(黑色符号数据中其实还含有蓝方符号的数据),最简单的方式就是做偏置。如果使用线性模式能够实现这样的一个二次方差的方法,那么能够保证在P跟U当中的损耗是一样的,所以在实验当中我们也证明了这样的方法是很有作用的。

PNU数据
接下来我们介绍一下PNU (Positive, Negative, Unlabeled)分类,就是正类、负类和无标签数据的分类。PNU分类其实就是一个半监督的学习方法。
现在我们对于PU分类学习有了解决方案,对NU分类学习也有自己的解决方案,所以PU跟NU基本上一样的。PN是一个标准的方法,我们也有相应的解决方法,对于PU、PN和NU分类学习中能不能使用半监督的方法,我们是希望能把其中的两者结合起来,就是蓝点或黑框或者红叉和黑框结合起来。
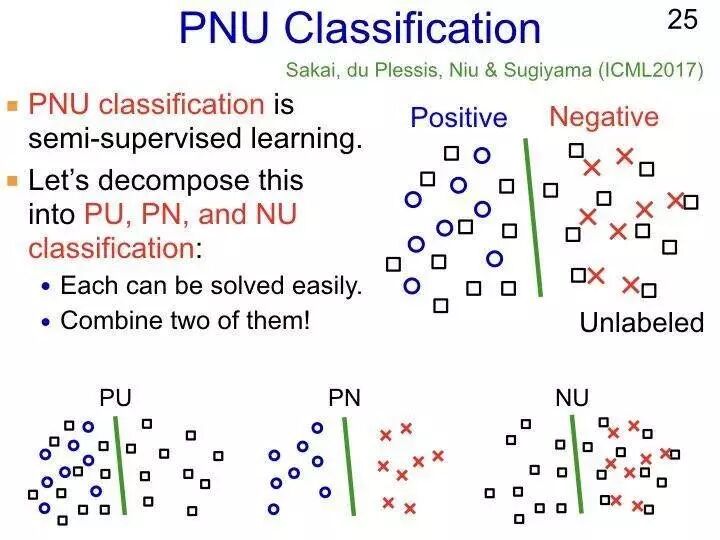
根据理论上的风险均值来看,如果在损失风险上PU比NU做的好的话,如果PN放在中间的话,会不会做的更好?或者另外一个方向,如果NU比PU做的好,那PN就放在第二位;或者说是PU放在第一位,或者PN放在第一位。
最简单就是PU和NU要把它结合起来,我们要把这两者整合起来。所以原理就是,第一步把PN和PU结合起来,第二步把PN和NU结合起来,这样的话我们总是能获得最优的方法,这是我们现在做的一个研究工作。
所以,我们的方法就是把它们结合起来,进行一个组合,根据我们自己假设性的数据进行切换,如果 是零,那就是变成一个PN分类学习,如果是
是零,那就是变成一个PN分类学习,如果是 是负,那就加上PU学习,如果
是负,那就加上PU学习,如果 变成正数我们就加上NU学习。后续继续选择,基本上在三者之间自由组合,添加一个不同PN、PU和NU的组合来实现自由分类。
变成正数我们就加上NU学习。后续继续选择,基本上在三者之间自由组合,添加一个不同PN、PU和NU的组合来实现自由分类。

我们再来看一下泛化误差边界:所有的数据和类型其实已经看到了,最后NU一个错误率这边还是存在的。换句话说,如果我们能够使用未标注的数据,哪怕没有簇假设(一个聚类簇对应一个标注类别)也能够控制泛化误差在一定合理的范围之内。一开始我们无标注的数据只是对它进行一个传播,但是这样的一些无标注数据,更多只是用于这样的损失和评估,而并不适用于正则化。

我们现在应该可以做一些类似平滑的正则化,这边其实并不好解释,也就是说可能在无标注数据当中获得标注数据。如果我们和其他的一些标准方法做一个比较的话,这样的一个PU加NU,PN加PU的方法所取得结果是非常好的。

互补型标准类别
最后我们来看一下相互补充型标注类别 (Complementary Labels) 的分类方法。
先来看一下类别更多的问题,也就是说现在可能是有1000多或更多类的分类问题。因为如果在1000个不同的标签当中来选择一个正确的标注类别描述这个类的话,其实这是很耗时的,这时候需要互补的标注类别。
我们选择其中的一类,就是错误的一类。这个做起来就简单了,1000类个候选当中,我们只需要把它随机抽选,如果说这个是错的话,那么我们就选,如果是正确我们就不选,我们选下一个,换句话说我们只选择错误的,帮助我们更快的选择最后正确的那一类,这个算法对于我们来也非常具有借鉴意义。
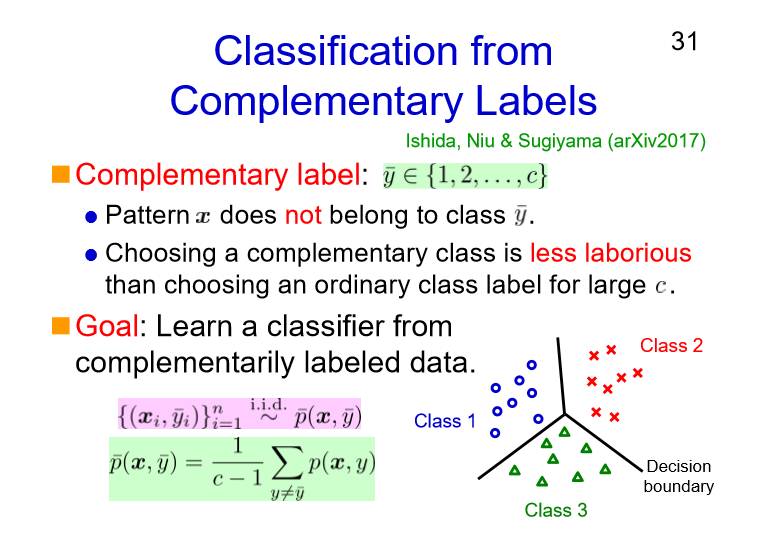
换句话说,其实就是使用类别的互补性,更容易选择大样本正确的类。我们现在假设是这样的,正常的标签,都是来自于p(x, y),但是是互补标签。所以,从这样的假设来看的话,我们没有办法确定它这样的一个一般性的标签和我们互补标签到底应该是以什么样的方法选择,但是如果说我们定好了这样的一个公式的话,我们就可以从互补标签的分类当中进行学习。
第一种方法,我们使用部分的标签来做分类,我们会有这样的一个多候选类,对于每一个互补标签的话,都会设置一个极端的情况,也就是c,所有的c我们都会给一个互补标签,一直把它从c一直到c-1;第二个办法可能并不是特别正确的办法,我们可以考虑多标签的分类的方法去做。在这个设置当中,每一个样本都会属于多个不同的类,也就是说对于互补类和正类的话我们都会使用的一个负标签,这个办法可能目前来说并不是特别好,但是有可能做的更好,总的来说,我们希望能够用更简单的办法来解决这样一个问题。

接下来可能就有点复杂了,假设我们做c类的分类,我们把R(f)和gy拿出来,gy就是单个class的分类风险,我们会对这个分类风险进行一个分析,今天我只举其中的一个风险的分析的公式。我们把两个分类进行对比,然后去算它的损失,我们会有这样的一个程度对称性的损失,就得出它的风险。
但是这个定义来看,在我们的设置当中没有这个样本量,所以要实现一个点对式对称损失函数 (Pairwise Symmetric Loss),我们就需要一定的特定条件。
我们可以用这样的一个公式表达它的风险函数,重点在于说不要取代P要取代P-,我们要把P-替代掉。所以,只需要把P-进行替代之后就可以对比它的一个损失风险。
但是有这样一个问题,这样的一种对称性损失,它只是用于一些非凸函数,换句话说,从数学层面来说你无法处理凸函数的情况,尽管我们绝大部分研究的场景都是非凸的场景。通过这样的办法,我们可以预测错误率(从公式当中可以看到),也可以看到,标注类别的互补性其实可以帮助我们实现最优的参数收敛率,这就是一个很好的例子。

随后我们做了相应的实验,我们所提出的方法在这里,部分标签数据互补数据都在这边用,我们只会使用1除以(c-1),如果我们有10类,如果你说不是1类,可能正常样本是第10类,换句话说最起码有9个互补标签,不是两个三个四个,需要C减1,10减1,需要9个互补标签。我们的方法应该算是最好的,就算是和右手边最常见、最主流的方法来比,我们做的更加的好,以上就是我们的实验结果。
最后我们做一个总结,我们最关注的是底下的这栏,也就是高精确性,但同时也希望需要的标注成本能够尽量的低。我们在UU、PU、PNU和互补性标签分类上,都希望能够实现高精度低标注成本的目标。
最后,介绍一下我所在的研究中心
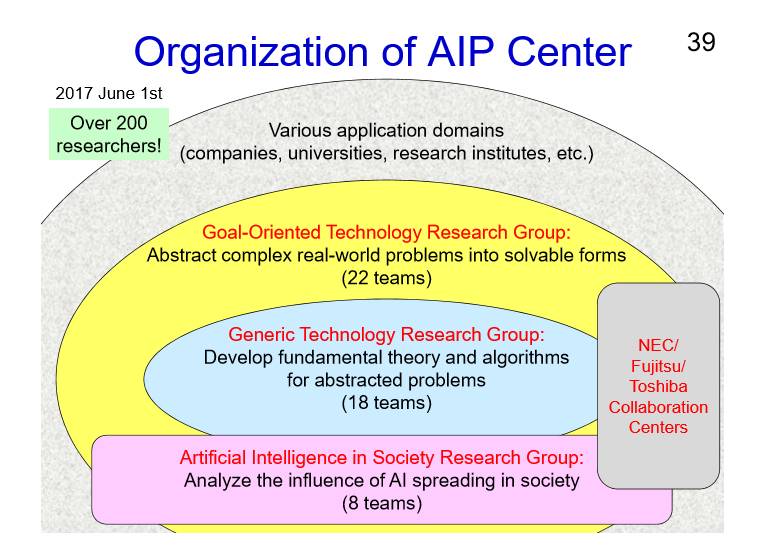
最后介绍一下我所在的研究所,日本理化研究所先进智能研究中心,也就是AIP。我们所关注的更多是先进的、智能的研究项目。在2016年的时候我们就成立了这个研究中心,我们有5个任务,分别是开发下一代的AI技术、加速科学研究、把AI用于决策日本的社会重大的问题,以及研究AI道德、法律和社会问题的问题,还有希望解决人力资源发展。

研究中心有三大集团,我们只关注基础的研究,所有的应用都是和合作伙伴付诸实施。目前我们目标的导向型技术研究集团,让更多的技术人员和产业量化人员在这边工作。对于我们来说,更多只是关注最基层的基础的AI的研究,还有一个组是我们AI社会研究组。我们有很多的合作伙伴,像大学、公司等,在中国也有很多很好的大学进行合作和联系,我们希望能有机会邀请诸位去我们日本的智能研究中心去看一看。
计算资源对于我们来说也非常的重要,我们决定购买了24台NVIDIA DGX-1,我们在Green 500列表上排名第4,我们现在能实现10.602个千兆次的计算能力。我们的办公室在东京,和火车站非常近,东京站走过去就可以看到我们的大楼。我们在大楼的15楼,入口是这样的,在内部我们有一个非常开放的讨论空间,也可以邀请来自学术界、研究机构的客人过来进行讨论。

下一次大家如果有机会来东京,可以到东京站,走10分钟的时间就能够看到我们的研究中心,希望我们可以有机会探讨交流,谢谢大家。
在人工智能头条(AI_Thinker)微信公众号会话回复“CCAI”,打包下载本次大会嘉宾演讲PPT。
CCAI 2017更多精彩内容,请关注微信公众号“AI科技大本营”,一次掌握“现场微信群”、“图文报道”、“PPT下载”以及“大会期刊”所有入口!















