“
今天大小吴来和大家聊一聊
最大公因数
的前世今生。
1 什么是最大公因数
最大公因数（Greatest Common Divisor），也称最大公约数、最大公因子，指两个或多个整数共有因数中最大的一个。
,
的最大公因数可记为
或
，多个整数的最大公因数也有同样的记号。求最大公因数有多种方法，比如我们小学就学过的质因数分解法、短除法。
短除法求最大公因数
那么你是否有这样的疑问：追本溯源，最大公因数最早出现在哪里呢？
2 欧几里得与辗转相除法
欧几里得（约公元前330年—公元前275年）
实际上，最早系统研究最大公因数问题的是古希腊数学家欧几里得。只不过那时还没有系统的代数学，相对应地，几何学明显地从数学中分离出来，并在希腊科学中占统治地位，其威力之大，以致于纯算术的或代数的问题都被转译为几何语言。
而欧几里得在《几何原本》第Ⅶ卷中正是运用了线段及其长度解释了最大公因数问题，并凝练出了世界上最早的算法——辗转相除法（也称欧几里得算法），具体可见定义Ⅶ.12、命题Ⅶ.1和命题Ⅶ.2.
“
定义Ⅶ.12：只能被作为公约的一个单位量所测尽（整除）的几个数称为互质数。
“
命题Ⅶ.1：设有不等两数，从大数中连续减去小数直到余数小于小数，再从小数中连续减去余数直到小于余数，这样一直下去，如果余数测不尽其前一个数，直到最后的余数为一个单位，那么该二数互质。
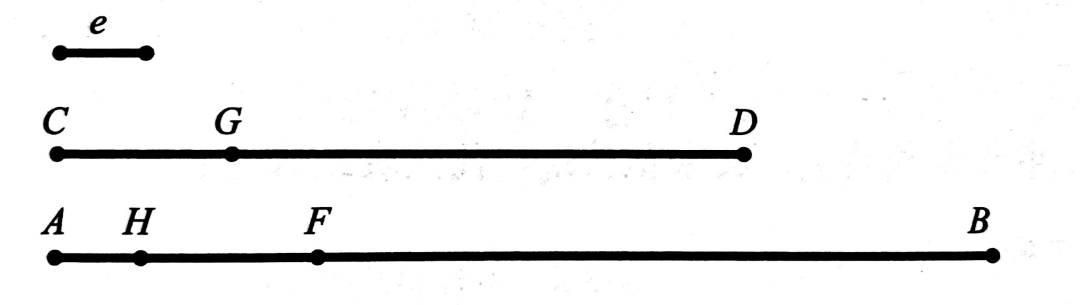
如上图，有两不等数
和
，连续从大数中减去小数直到小于小数，再从小数中连续减去余数直到小于余数，这样一直下去，余数总是不能测尽前一个数，直到最后的余数为一个单位。
求证：
和
互质，即只有一个单位能测尽
和
.
证明：如果
和
不互质，那么总有某个数测尽它们，令其为
（这里
）.
令：
测量
得
，余下
小于
. 令：
测量
得
，余下
小于
. 令：
测量
得
，余下单位量
.
因为
测尽
，
测尽
，所以：
测尽
.
又因为
测尽
，所以：它测尽余值
.
同理可得
也可以测尽余值
.
最终可得
可以测尽单位量
，这是不可能的，因为
而
。
因此：
和
只能被作为公约的一个单位量所测尽，即：
和
互质（定义Ⅶ.12）。
-
现代数学语言已经不再沿用欧几里得在《几何原本》中的术语了，“测得”、“测尽”两个词已用“除”、“整除”代替。这一命题的证明已经运用了辗转相除法：开始于两个数，从较大的数中重复减去较小的数，只不过这里为了说明两数互质，它假定1是辗转相除法的最终结果。
“
命题Ⅶ.2：给定两个不互质的数，可以（用辗转相除法）找到它们的最大公因数。
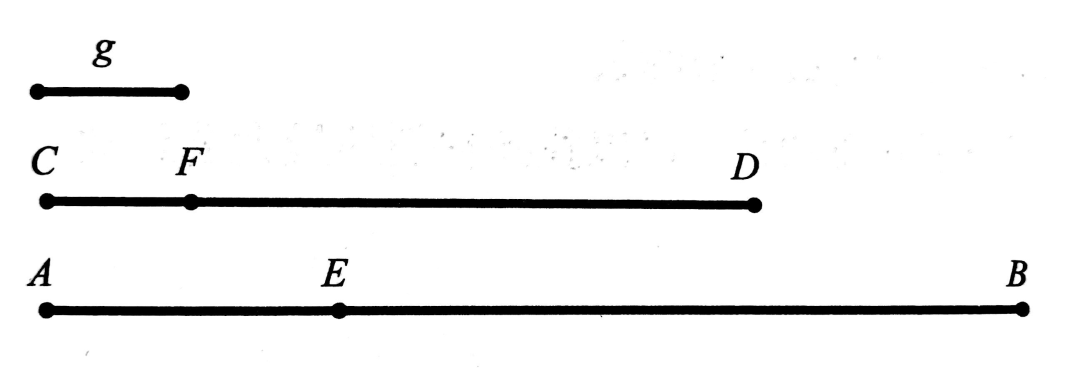
如上图，设
和
为给定的两个不互质的数。现在要求的是：找到
和
的最大公因数。
这里需分类讨论：
①如果
能测尽
，则
必然是
和
的最大公因数。
②如果
测不尽
，那么：就用余数去量
，如果量不尽，又用后边的余数去量前边的余数，直到后边的余数测尽前边的余数。
这最后的余数不是一个单位，否则
和
互质，这与假设矛盾。所以：某数可以测尽它前面数的余数。
这里和命题Ⅶ.1的操作类似，
测
得
，
测
得
，设最后
测尽
.同样地，可推得
同时测尽
和
，即
是
和
的一个公因数。
以下进一步说明它一定是最大的。
如果
不是
和
的最大公因数，那么必有一个大于
的某数
同时测尽
和
.
那么，因为
测尽
，
测尽
，所以
也测尽
，又它测尽整个
，所以它测尽余值
.同理，
测尽余值
，但这是不可能的，因为较大数不可能测尽较小数，矛盾。
所以没有大于
测尽
和
的数，即
是
和
的最大公因数。
-
在这一命题中，再次使用了辗转相除法求两个不互质的数的最大公因数，大数反复减小数，直到余数小于小数。比如要求
，首先，从104中反复减去40，直到余数（24）小于40，即
再从40中反复减去24得余数16，即
再从24中反复减去16得余数8，即
最后停止，因为8可以整除16.于是我们找到了
这里其实也可以用图形来解释这一过程：如图是边长为40和104的矩形，求
