 本
期由静电纺丝学术前沿供稿,纳米人编辑部补充和丰富。
本
期由静电纺丝学术前沿供稿,纳米人编辑部补充和丰富。
欢迎投稿:[email protected]
原道专栏 第2期
Science是国际顶级学术期刊,但是偶尔也会发表一些“似乎水平不怎么样”的研究成果,俗称“灌水”。每当遇到这种情况,就会有人出来抱怨大牛们的不公平。或者,回忆起这想法我也有过,可惜做了一段时间就停下来了,因为觉得做不下去了。那么,为什么一些“似乎水平不怎么样”的研究成果能够发表在Science呢,难道Science是傻的吗? 难道Science聘用的100多位评审编辑是做摆设的吗?
今天,我们以最近的一篇Science文章为例来解析一下:为什么同样的工作,别人能发到Science,而我却不能!

原文链接:http://science.sciencemag.org/content/360/6386/296
2018年4月20日,Science在线发表了一篇关于电纺纳米纤维的文章。第一眼看上去,文章报道的其实只是一个非常普通的现象,通过毛细力诱导折叠实现浸湿态纳米纤维膜的大尺度形变。我不禁一声叹息,怎么又是别人家的成果!同样的东西,别人怎么就能玩得这么高大上呢!!!
做科研,首先要有好奇心。为了弄清楚这篇Science到底有什么厉害之处,我于是认真研读了本文,下面请让我对文章进行深度解析,看别人是怎么把一个普通的现象玩上Science的!
静电纺丝技术,我猜大家应该都知道吧。简单来说,静电纺丝技术是一种材料加工技术,能够制备出直径从几纳米至几微米的连续纳米纤维。
PS:其实,熟不熟悉静电纺丝也没关系,这篇文章只是研究基于电纺纳米纤维膜的一种现象。
相信做电纺的小伙伴们一定有把纤维膜泡进水里的经历吧,很多时候都是形成一坨类似鼻涕一样的东西吧,黏糊糊,恶心至极。也许还有小伙伴们做过电纺纤维膜的浸泡处理,或者是dip-coating处理。处理完后,如果处理不当,烘干后膜会收缩、变皱得厉害。
这篇文章研究的正是这个电纺纤维膜收缩的现象。
首先,我们来看看具体的现象吧,先从图片看起,这膜确实是够平整:

图1
:
纳米纤维膜的收缩现象
:
A
,电纺PVDF-HFP纳米纤维膜(纤维直径300 nm, 膜厚度大概几微米);
B
,将纤维膜用硅油润湿,用8个夹子支撑拉平;
C-E
,将夹子平台向中间收缩靠拢,可以看到虽然膜的面积在减小,但始终没有松弛和下垂,而是保持平坦的状态。其原因正是文章作者要研究的wrinkle和stack现象,(编注:wrinkle译为褶皱,可以理解为小幅度的收缩;stack译为折叠,可以理解为大幅度的收缩重叠);
F
,局部放大图可以看到产生的褶皱。另外文章作者把这种收缩的褶皱称之为“membrane reservoirs”
但是,如果仅仅停留于发现了这个现象,显然是不够的。一个idea要凸显其重要性和与众不同,就必须要有重大的研究背景和应用价值。那么,这篇文章的作者,是怎样体现其重要性的呢?
仿生,是近年来常用的高大上背景和灵感来源,屡试不爽。本文作者煞费苦心,走的也是这个套路,文章一开头introduction便铺陈了一大段排比,列举了多个仿生现象:
1)某种蜘蛛丝(ecribellate spiders)能够拉伸高达10000%,而且在任何状态下都保持直线状态;
2)细胞能够伸缩,比如巨噬细胞能够吞噬自己体积5倍大的细菌或细胞残片;
3)T lymphocytes细胞能够拉伸40%挤进微血管中;
4)10微米宽的神经元细胞能够伸出数百个微米尺寸的neuronal projections;
5)纤维母细胞的渗透膨胀能够导致70%的体积增大。
然后,作者反问:为什么这些细胞能够承受这么大的形变呢?那是因为细胞膜是褶皱的并且有大量的微绒毛。然后,作者在introduction里进一步描述了可拉伸材料的各种潜在用途,比如柔性电池,智能织物,生物医学器件,组织工程,软体机器人等等。
不得不承认,作者的知识面之广,眼界之宽。一口气上来这么多例子和应用,换作是我,绞尽脑汁也想不出这些啊。
更厉害的是,作者接下来展开了高深的mechanics建模分析。各种公式、模型,对于学化学的我来说,看的是云里雾里,不知所云,反正觉得很高大上就是了。
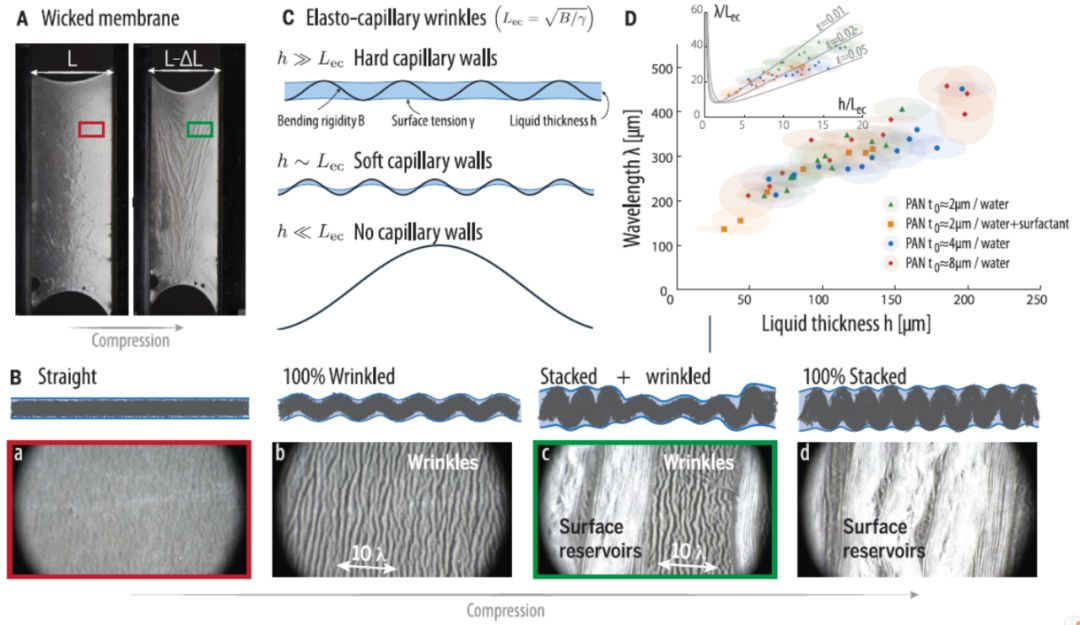
图2
:
毛细力诱导的褶皱和折叠的mechanics分析
:
A
,水浸湿的电纺聚丙烯腈(PAN)纳米纤维膜,宽度L=4 cm,两边固定在移动的平台上。可以发现两边靠拢时纤维膜有明显的褶皱图案。(注,文中用的wicked membrane来形容这个纤维膜,具体也不好准确翻译,意思应该是纤维膜吸水后通过毛细力发生了收缩褶皱,暂且直接称之为浸湿的纤维膜或者液态膜);
B
,一系列显微照片显示纤维膜收缩的状态和过程(a 平坦没有褶皱状态;b 100%褶皱(wrinkled)状态;c 同时存在褶皱(wrinkled)和折叠(stacked)的状态;d 100%折叠(stacked)状态);
C
,褶皱过程的物理解释:当液态膜厚度(h)和弹性毛细力长程(elasto-capillary length, L
ec
)不同大小关系的三种情况;
D
,液态膜厚度h与褶皱波长
λ之间
关系的实验数据。
首先,作者通过显微镜观察了纤维褶皱的形貌,如图2B所示。对于观察到的褶皱,作者又用了几个形象的比喻:褶皱的皮肤,干瘪的水果,大脑沟壑,悬挂的窗帘等。
然后,作者通过一个简单的模型分析了这个褶皱的现象。(注:这个模型忽略重力的影响,因为他们发现重力仅仅会对发生褶皱的方向产生影响。)用到的几个物理量包括:
褶皱的波长:wavelength,λ
界面张力(表面张力):interfacial tension,γ
纤维膜的厚度:fibrous membrane thickness,t
0
液态膜的厚度:liquid film thickness,h
膜的抗弯刚度,bending stiffness,B
弹性毛细力长程,elastocapillary length,Lec=(B/γ)
1/2
这个模型系统考察的重要参数是:h/L
ec
当 h/L
ec
<< 1 时,就是我们日常能够观察到的现象,比如浸湿的纸张和布,这时候表面张力基本可以忽略,因而纸或布不会发生褶皱;
当 h/L
ec
>> 1 时,就会发生文章所描述的褶皱的想象。这时候表面张力不可忽视,强的毛细力会驱使纤维膜发生收缩褶皱。
具体的模型分析支撑材料里有大量的公式推断分析,感兴趣的读者可以去看看。反正我是一看到各种数学公式就犯晕。
接下来,作者进一步拓宽思维,考察了不同形状的情况,比如二维平面,圆筒状,以及球状的收缩折叠情况,如图3中所示。他们观察到了同样的现象,即,虽然他们的面积或体积在收缩,纤维膜的表面依然保持“平整”。
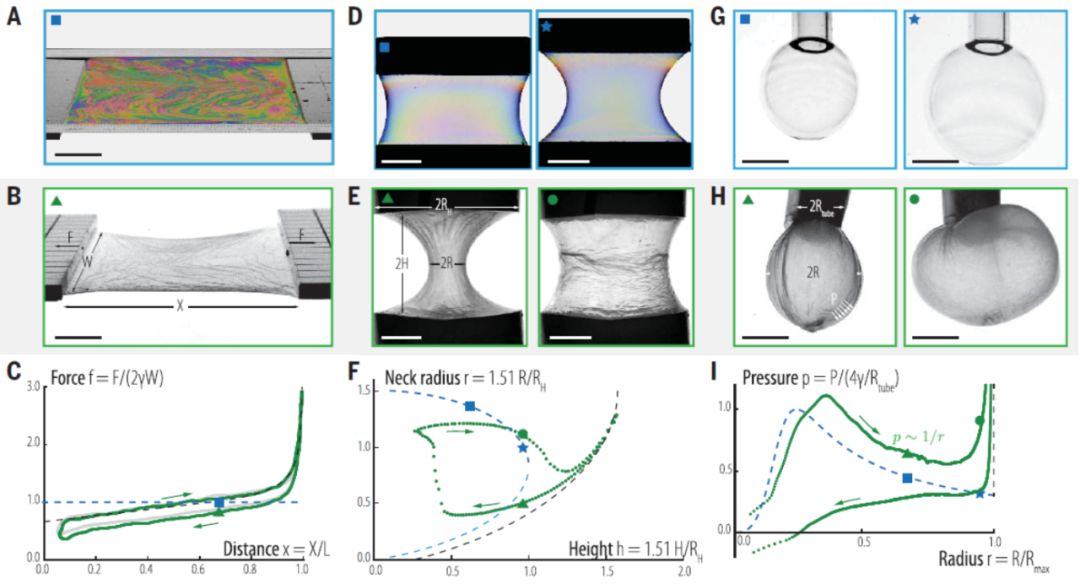
图
3
:
不同形状纤维膜的情况:
A
,
D
,
G
为用肥皂水形成的平面,圆柱,和球状的收缩情况;
B,E, H
为用浸润纤维膜(PVDF-HFP)形成的平面,圆柱,和球状的收缩情况;
C,F, I
为B, E, H对应情况参数的考察分析。
为了让大家看得更直观,上几个视频吧:
视频1
. 二维平面纤维膜收缩情况
视频2
. 圆筒状纤维膜收缩情况
视频3
. 球状纤维膜收缩情况
最后,作者们展示了两个潜在的应用:1)表面功能化;2)可拉伸电路。如下图4所示:
1)用电纺纳米纤维膜将一个锆珠包住,可以看到没有包裹纤维膜是锆珠表面不能被红色的水浸染(a);当用亲水性的PAN纤维膜包裹,在水中浸泡拿出后,被均匀地浸染(b);当用疏水性的PADF-HFP纤维膜包裹,则不能被水浸染(c)。
2)在电纺PVDF-HFP纳米纤维膜表面粘附上100 nm厚的金(Au)作为导线并连上LED灯泡,从而实现可拉伸电路的设计。
其实在笔者看来,这两个应用实在是有点牵强附会:
第一个应用貌似跟那个褶皱的现象毫无关联,完全取决于纤维膜的亲疏水性。而且这种表面纤维包裹功能化的处理完全不会比使用简单的表面修饰方法稳定牢固。
对于第二个应用,也存在一定的问题,首先,这个纤维膜必须是浸润状态才具有拉伸性,浸润液体肯定会对电路有所影响,因而没什么实用价值;其次要在厚度几微米的纤维膜表面牢固地沉积导电金属材料必定操作困难。






