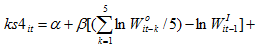
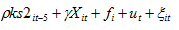(1)
外部工资
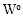采用过去五年学校周围30公里内非体力劳动者的对数平均工资，教学成效一时半会很难看出来，所以用滞后五年的平均工资来体现，同理内部工资
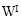也采用了一阶滞后。选取30公里是因为太近如学校周围10公里，很可能是人们择校的自选择结果，好学校经常能吸引高收入的家庭来周边居住和工作，因此有内生性。在文章图二里面作者绘制了TTWA（工作通勤区域）对学生成绩的影响图，发现在20-60公里内结果都是显著为负的。由于超过60公里可以认为超出绝大多数教师的通勤距离，不会对其工作选择产生多大影响，因此通勤距离这个变量是高度稳健的。由于英国的secondary通常是五年，老师经常会同时承担五个年级的教学工作，t期发生的冲击可能会同时影响所有年级的学生，导致不同年级学生成绩之间存在高度的序列相关，因此作者进一步控制了五年前不在同一所学校的ks2成绩以避免遗漏变量造成的序列相关及内生性。由于2008年以后英国各地对公立学校工资管制开始放开，因此本文选择的最终有效样本只有2002和2007两年，在附录A1中给出了本文所有变量的来源和起止时间。控制变量X包括性别比例male、免费午餐学生比例fsm、特长生比例sen和生均支出epp等，f
i
和u
t
是学校和时间固定效应。
如果上述模型把右边的ks2移到左边，因变量是Δks=ks4-ks2，对估计结果会有什么变化,此时估计结果应该如何解释？最直观的就是变形后的差分方程相当于对原来的（1）式施加了ρ=1的约束。但是要透过现象看本质，必须利用rubin的潜在因果模型分析框架。这个问题在现在被称为lord's paradox，对这个问题感兴趣的朋友可以看厦门大学赵西亮老师新出的《基本有用的计量经济学》以及人大江艇老师的讲义。后面的这段论述，很大程度上参考了江艇老师的讲义，在此表示感谢。
要识别出真实的ATT（E（y1-y0|D=1））,如果是变形后的差分模型，则估计的β=[E(y|D=1)-E(x|D=1)]-[E(y|D=0)-E(x|D=0)],相当于假设
[E(y0|D=1)-E(x|D=1)]-[E(y0|D=0)-E(x|D=0)]，也就是处理组（受到严格工资管制的学校）如果没有接受处理，其学生成绩的变化与控制组（没有受到严格工资管制的学校）相同。如果是本文的原模型（1），则估计的β=[E(y|D=1)-E(y|D=0)]-ρ[E(x|D=1)-E(x|D=0)],则相当于假设[E(y0|D=1)-ρE(x|D=1)]=[E(y0|D=0)-ρE(x|D=0)],即如果未接受处理，受到严格工资管制的学校与ks2成绩相同，但没有受到严格工资管制学校的ks4成绩相同；且[E(y0|D=1，X=x)=[E(y0|D=0，X=x)=a+bx,即受到严格工资管制的学校在没有接受处理时ks4和ks2之间的线性关系与没有受到工资管制的学校相同。如果比较这2个假设，我们发现差分模型其实就是DID的平行趋势假设，相比原模型需要同时满足2个假设理论上更弱些。此外通常说来，受到严格工资管制的学校都是教学成绩质量较差的学校，因为好学校有钱给老师发额外津贴以留住好老师，他们在放松工资管制时学生成绩的提高也会比通常不容易受到严格管制的好学校学生成绩提高慢，因此差分模型通常会低估ATT。而容易受到严格工资管制的差学校正是因为教学质量差，生源不好，如果在遇到与不容易受到严格工资管制的好学校具有相同ks2成绩的好苗子时，会对其重点培养，因此原模型通常会高估ATT。本着应用计量“系数不怕低估，标准误不怕高估”的原则，本人认为采用差分模型设定应该会更好，当然这是本人的一些不成熟看法，欢迎各位朋友批评指正。
2.基本估计结果
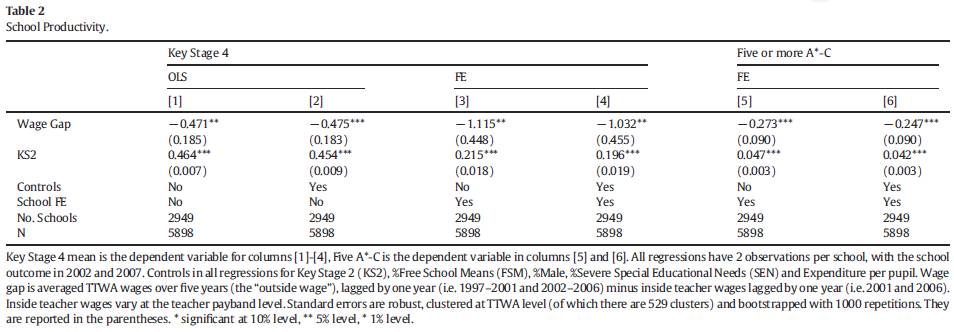
如表二所示，无论是否控制学校固定效应，是否加控制变量，无论因变量是ks4成绩还是5a以上成绩比例，工资管制越严格的学校，与外部的工资差距越大，会对学生的学习成绩产生十分显著的负向影响。这说明什么，要想孩子学习成绩好，赶快给老师加工资啊，这是多么明显的经验证据啊，真希望我们领导人能看到。为了让大家相信这个结论，作者接下来做了大量细致稳健性分析工作，非常值得我们学习。
3.稳健性分析
A.差分是否能消除学校固定效应？
由于本文样本不连续，02年和07年入学的学生各方面差异比较大，所以可能有些同时随学校和时间变化的不可观测因素会对教师工资和学生成绩产生影响，这就不只是单独控制学校固定效应所能捕捉的。为了检验这一点，在附录A4中将学校工资增长率对着性别比例male、免费午餐学生比例fsm、特长生比例sen等可观测因素回归，发现无论是单个变量还是整体都不显著，因而类似RCT和RD的平衡性测试原理，间接论证了工资变动和不可观测因素也不相关。个人认为这里进一步控制不同学校的线性趋势（学校固定效应交互时间趋势项）可能会更好，因为上述用来做测试的变量其实就是模型1中的控制变量，如果关注的核心变量跟控制变量不相关，从估计系数角度看不会影响无偏和一致性，只是可能会使标准误更小点，估计变得更精确。表二的第1列和第2列、第3列和第4列、第5列和第6列之间系数十分接近也说明了这一点。
B.平行趋势检验
如前模型设定中所述，（1）式类似在做工资管制政策改革的DID估计，因此需要进行平行趋势检验。如果工资变化与学校初始特征相关，就会使得之后的工资变化与某些不可观测因素相关，从而平行趋势不满足。因此作者在附录A5中在地区而不是之前的学校层面，用工资增长率分别对02年初始特征（02年的性别比例male、免费午餐学生比例fsm、特长生比例sen）、ks4成绩、5A以上成绩比例回归，结果都不显著，从而支持了平行趋势假设。
C.安慰剂检验
如果确实是因为学校工资比外部市场低，从而影响了老师的教学积极性，导致学生成绩下降的话，那么如果换成是与教师脑力行业不大相关的体力行业的工资作为外部工资，这个时候影响应该更小和更不显著，表三第二行的回归结果证明了这点。
D.学校间博弈影响
由于ks4成绩是教育局对各学校的一个重要考核指标，因此各学校也有动力通过减少考生人数和次数来提高平均成绩，因此表三的第八和第九行用排除考试的人数和参加考试的次数作因变量回归，发现确实工资差距大的学校有通过减少考试次数来提高平均成绩的动机。
4.异质性分析
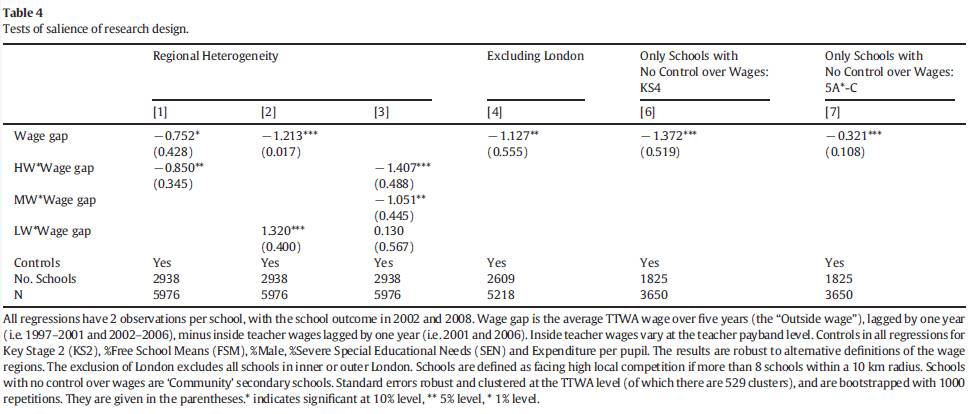
作者又将高、中、低收入地区虚拟变量与工资差距交互，如表四的第1、2、3列，发现在外部收入越高的地区的学校的学生平均成绩越差。然后用对工资完全没有自主控制权，也就是工资管制最严厉的社区学校样本进行回归，如表四的第6、7两列，发现无论系数还是显著性都更高。
5.机制分析
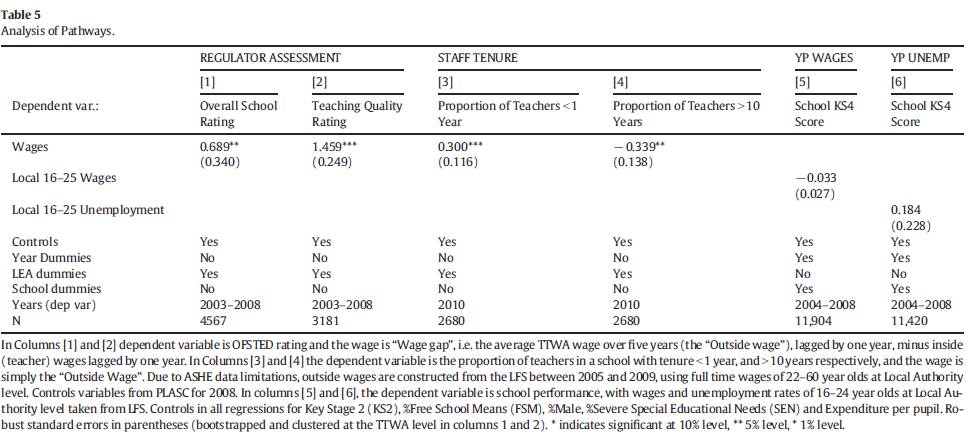
除了通常认为的工资差距会通过教师的努力程度和优秀老师的供给影响学生成绩，本文表五的第1、2、3、4列分别通过对学校的总体排名、教学排名以及老师在校工作时间回归，证实了上述机制。此外作者还认为学生和家长对工资变动的反应也是影响学习成绩的重要原因。第5、6两列通过k4成绩对当地16-25岁的平均工资和失业率进行回归，发现好的工作条件（高工资和低失业率）不会使学生在学习时分心而影响学习成绩。
