
弃九法猜数游戏之一
我们知道,习以为常的十进制数有着一个有趣的特性,
一个十进数除以9所得到的余数,等于这个十进数的各个数位上的数的和除以9所得到的余数。
根据这个特性,既可以进行验算(俗称
弃九法验算
),也可以进行猜数游戏。现在,从一则颇为动人的故事谈起。
古代的波斯国,有个国王是数字迷,一天,有一位少年求见国王,说是要献上一道有趣的数学游戏。国王召见后,这位少年说道:“国王,请您背着我任意写出一个不少于两位的正整数,再用它减去这个正整数各个数位上的数的和,然后再所得的差中随便圈起其中一个不为零的数字,把剩下的数字逐个告诉我。我便能立即知道您所圈起来的是一个什么数字。”
国王不解的说:“你怎么知道我随便圈起来的那个数字呢?”
“国王如果不信,可以立即验证。”这位少年满有把握的说。
于是,国王背着少年写下了一个七位数7540876,让别人用它减去各个数位上的数的和。(7+5+4+0+8+7+6=37),得7540876-37=7540839。接着国王在所得的差中把3圈起来,说道:“我已经按照你的说法做了,剩下的数字是7,5,4,0,8,9,你知道我圈起来的是一个什么数字吗?”
“知道!国王您圈起来的是3。”少年立刻回答道。
国王感到很惊讶,他怎么知道呢?当这位少年把其中的奥妙告诉过王后,国王对这一奇妙的数学游戏很感兴趣,于是重赏了这位少年。这位少年是怎样推算出来的呢?
这是一个有趣的数学游戏。
只要把圈后剩下的各个数字加起来(或者不必加上0与9),看看还要再加上一个什么一位数。正好是9的整数倍,那么这个数就是被圈起来的那个数。
这里,7+5+4+0+8+9=33,或7+5+4+8=24,都是再加上3,正好是9的整数倍,所以被圈起来的数是3。
弃九法猜数游戏之二
在整个游戏的过程中,老师面向学生,始终不看黑板,老师先请一位学生在黑板上随意写出一个多位数,例如7516726。然后,再请一位学生把刚才所写的数随意打乱排成另一个数,例如,2176567,接着,计算这两个多位数的差(大数减小数),7516726-2176567=5340159。最后,请一位学生在差中随意划掉一个非零的数字,并把余下的数字按任意次序高声读出,例如,划掉一个数字5,读为534019,这时,老师便能正确迅速地说出学生划掉的数字是几(5)。
这个游戏的奥秘在哪里呢?我们知道,一个多位数除以9所得的余数等于这个多位数各个数位上的数的和除以9所得的余数。因此,
随意写出的多位数与后来据此打乱排成的另一个多位数,它们除以9就具有相同的余数,它们的差(大数减小数)是9的倍数。
这就是说,差的各个数位上的数字的和是9的倍数。所以,在差中随意划掉一个非零数字后,便能猜出被划掉的数字。
例如,在上例中,老师把学生高声读出的数字,用心算加起来,得
5+3+4+0+1+9=22
,再把这里各个数位上的数相加,直到得到一个数字为止,
2+2=4
。甚至,可以这样地心算:不必加上
0
与
9
,得
5+3+4+1=13
,再把这里各个数位上的数字相加,直到得到一个数字为止,
1+3=4
。这里所得的数字是
4
,说明被划掉的数字是
5
。添上这个数字
5
后,差就是
9
的倍数。
弃九法猜数游戏之三
(扑克牌游戏)
老师把一副扑克牌的大王、小王拿起来,同时说明每张牌代表一个数:2,3,4,5,6,7,8,9,10就代表本身所标明的数;J,Q,K和A分别代表11,12,13和1。接着,老师按黑桃、红心、梅花、方块4种不同的花色分别发给甲、乙、丙、丁4个学生。每位学生一种花色,都是13张牌。让他们各自将这13张牌任意分为若干组,每组的张数是随意的,然后计算每组各张牌所代表的数的和。在这些所求的和中任意删掉一个数字,将剩下的数字告诉老师。老师就能很快地说出被删掉的数字。
例如,学生甲的分组演算如下:
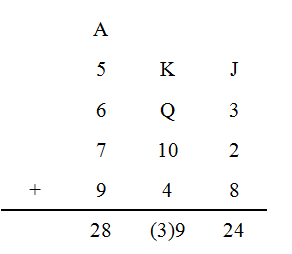
甲将其中的一个数字3删掉,告诉老师2,8,9,2,4五个数字,老师很快地说出了被删掉的数字是3。
学生乙的分组演算如下:

乙将最后一个数字6删掉,告诉老师2,5,3,4,2,6六个数字,老师也很快就说出了被删掉的数字是6。
学生丙的分组演算如下:
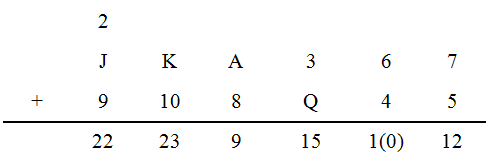
丙将其中的一个数字0删掉,告诉老师2,2,2,3,9,1,5,1,1,2十个数字。老师问道:删掉的这个数字比5大吗?丙回答:比5小,老师随之说出了被删掉的数字是0。
这里的奥秘是什么?
原来老师首先将学生告知的各个数相加(或者不必加上0与9),如果加得的和是两位数。再将组成这个两位数的各个数位上的数相加,使之成为一位数。然后用10减去这个一位数。
所得的数就是被删掉的数字。这里有一种情况必须注意:
当所求余下各个数的最后和为1时,被删掉的数有两种可能:9或0,遇到这种情况,可先问删掉的数比5大吗?若大于5,则为9;若小于5,则为0。
于是,甲余下各数的和是2+8+9+2+4=25。进而2+5=7,甲删掉的数字是10-7=3。乙余下各数的和是2+5+3+4+2+6=22。进而2+2=4,乙删掉的数字是10-4=6。丙余下的各数是2+2+2+3+9+1+5+1+1+2=28,进而2+8=10,1+0=1,丙删掉的数字比5小,所以这个被删掉的数字是0。
现在来说说这一扑克牌游戏的理论跟据。
我们知道,能被9整除的自然数的各个数位上的数的和必定能被9整除;反之,不能被9整除的自然数的各个数位上的数的和也必定不能被9整除。
这里的13张牌的和是:A+2+3+4+5+6+7+8+9+10+J+Q+K=91,9+1=10,1+0=1。由上述整除性质可以知道。这13张牌的和不能被9整除,且其余数必定是1。因此把13张任意分为若干组相加。所得各组和的各个数位上的数的和也不能被9整除,且其余数也必定是1。又因为两个非负整数的和为1的,有且仅有一种情况:1+0=1,从而可知各组和的各个数位上的数的和的最小两位数必定是10。
* 来源:《进位制与数学游戏》,李友耕著,科学出版社,有删改。
以数学学习为主题,以传播数学文化为己任,以激发学习者学习数学的兴趣为目标,分享有用的数学知识、有趣的数学故事、传奇的数学人物等,为你展现一个有趣、好玩、丰富多彩的数学世界。




