
文章
来源:数学中国
我是一个“西瓜控”,不管夏天还是冬天,都喜欢吃。要是一人独享西瓜的话,我都是一刀两半,然后拿勺子大口大口地吃,痛快。可是如果和家人朋友一起分享的话,那只好把西瓜切成一块一块的,大家一人一块的这么吃。可是面对西瓜,我总会邪恶地挑大块的吃,以免“吃亏”。如果两个人分瓜,一人一块轮流吃下去,谁会吃得多呢?又怎么才会吃得多呢?
你或许不知,这也是一个有趣的数学难题呢,虽然不像哥德巴赫猜想这么有名,但它也整整经历了15年才终于在去年被成功解决。
问题最早在1967年《数学杂志》上被提出,好事之人叫厄普顿(Upton),但他关注的不是分西瓜,老外嘛,爱分Pizza。因此问题如下:
如果有一个Pizza,经若干刀分成顶角相等的若干份之后,两个人按照顺时针(或逆时针)的顺序一人一块来吃的话,谁能吃得多呢?
这个问题看似很白痴,有人会说,每个人都取来自己分得的Pizza,然后称一下不就知道了吗?但这个问题在数学家眼中,却是另一个世界。

问题的开端:切2刀和切偶数刀
数学家磨刀霍霍,开始考虑各种情况。第一,如果每一刀都经过Pizza的圆心的话,那当然不管切几刀,两个人都会分到一样多。实际上人们分Pizza不可能精确地都切过圆心的,所以问题来了:如果每一刀交错点不在圆心上,那两个人谁能分的多呢?
显而易见,切两刀的话,那Pizza会分成四份
(见下图)
。如果两刀的交错点不在圆心,那么一定会有一块大一些,也就是包括Pizza圆心的那一块。结果不难推出:吃到Pizza圆心的那个人会分得更多Pizza,也就是图中白色的两块Pizza。
如果切4刀,6刀,8刀或更多的偶数刀的话,结果就有所不同了——两个人会分得一样的Pizza。
(见上
图)
这个问题并不是很难证明,不用很难的代数知识就可以解决。厄普顿也就是做了这个工作,分析了所有偶数刀的分发结果。可如果是切3,5,7,9刀呢?这才是真正难题的开始。厄普顿并没有研究这个,它也就一直沉寂到了1994年。
真正的难题:切奇数刀的话
数学家迪尔曼在1994年的时候同样是在《数学杂志》上再次提到了这个Pizza难题,并且邀请广大数学家们来解决:如果切奇数刀会怎么样?他自己计算了,如果切3刀的话,吃到Pizza中心的人会分得的更多。然后另一个数学家马布里加入了这个研究,他计算了切5刀的情况。结果正好相反,吃到Pizza中心的那个人会分得更少。如果继续计算下去,再增加两刀达到7刀的时候,结果又反过来了……每到下一个奇数,结果好像就颠倒一次。
(见下图)
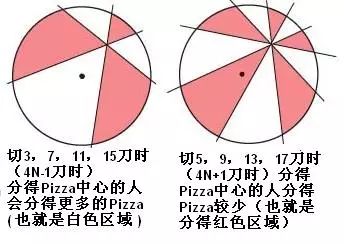
如何分析所有奇数的情况呢,这似乎才是问题的关键所在。迪尔曼和马布里两人由此展开了他们漫长的数学解密征途。这个问题看似简单,但是要做到严格的数学证明,并不容易,就像历史上那些著名的数学难题一样,需要精密而且精巧的方法,才能解决。
经过了漫长的15年,他们才终于征服了这个Pizza难题。15年,就研究了怎么分一个Pizza,听上去有点滑稽,但对于数学理论来说,这是一个不可忽视的贡献。具体的解决方法,我想我和大家都不能完全看懂,在此就不赘述,大致上他们把问题转化了一下:把“每多切一刀,两个人相比谁多谁少”由一个正负值的来表示。为了分析这个正负值是如何变化,他们需要一个代数模型来计算。经过多年来在无数的代数学已有的模型中辛勤搜索,他们终于从一篇1979年的论文中找到了所需的模型,然后问题迎刃而解。结论也就是——
切3,7,11,15刀(4N-1刀)时,吃得到Pizza中心的人会分得更多;切5,9,13,17刀(4N+1刀)时,吃到中心的人分得少
。















