如何排列国旗上的小星星

作者：蒋迅 王淑红

节选自《数学都知道》丛书第2册，有删改。

自古以来，人们对于星星都抱有敬畏和向往。人们甚至认为每一颗星星都是一个神灵。这种崇拜的心灵必然反映在人们日常的图案中。五角星就是星星的抽象表示。作为一个国家的象征，很多国家都把五角星镶嵌在国旗上。据徐传胜教授的统计，一共有至少55个国家的国旗上镶有少到一个多到五十个五角星。随着五角星的增多，五角星的排列就是一个需要考虑的问题了。这不仅是一个艺术的问题，而且是一个理念的反映；而其排列表达又可以引出一些数学问题。在这里我们就以五角星最多的美国国旗来说说这里面的数学问题。

1、 美国国旗上的星星排列问题

美国，全称为美利坚合众国，是联邦共和立宪制国家，有50个州，它的国旗上目前有50颗小星星，就分别代表这50个州。如果这是一成不变的事实倒也不必太费心思，问题是历史上，美国的国旗上的五角星的数目一直是和美国的州的数目相对等的。由于美国成立联邦的时候一开始就有13个州，所以现在这50颗小星星是从13颗开始一点点增加起来的。

当联邦政府正式成立的前后两年，美国国旗还不是星条旗。从1777年开始才有了五角星。而且一开始有几种不同的设计。曾有人设计了一个把一颗星星放在中间的图案，但没有被采纳。后来这个提案被修改成13颗星星形成的一个圆圈的图案。传说是一个叫罗斯的女子在获得了总统乔治·华盛顿的亲自授权后缝制的。这个故事无法证实，但如果读者到费城的话可以看到罗斯的房子。

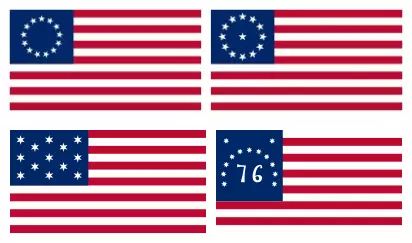
图1. 四种未被选中的13星旗

以后每当有新的州加入时，国旗上就增加一颗星（如图2）。而且每次有新的州加入，都要考虑如何排列国旗上的星星。迄今为止，最后一个加入进来的是夏威夷。世事难料，有谁知道以后会不会还有哪个地方突然会加入进来呢？这并不是杞人忧天，第二次世界大战结束后，有些菲律宾人就曾提出加入美国联邦。2012年11月有报导称，波多黎各公投，逾6成民众选择成为美国第51个州（他们甚至设计好了有51颗星星的国旗）。2014年1月，硅谷投资人德雷珀推出一项计划，将加州分为6个独立的州。所有这些信息，似乎都在预示，在未知的将来，美国真的会有不止50个州呢。

图2. 13州时图样之一：六角星旗、15个州时的国旗和加州入联邦时的国旗

最后使用的48星、49星和50星的国旗图案分别如下图所示（如图3）：

图3. 48星旗、49星旗和50星旗

于是出现了一个问题，如果美国确实有了大于50的N个州，那么国旗上的星星该怎么排列呢？按照美国的宪法，一旦有新的州加入联邦，联邦政府必须在美国独立日（即7月4日）之前将国旗更新。如果提前有一个大家都能接受的排列这些星星的方案岂不更为省事。

2.、数学家利用程序为美国国旗排列星星

美国人威尔逊想到了未来国旗上的星星该如何排列的问题，他自己没有解决，把问题抛给了数学家加里波第。加里波第不负所望，设计出一个程序，只要人们选择N为100以内的任何数字，这个程序就可以给出国旗上N颗星的分布图。他的做法是这样的：首先对历史上曾经在国旗上正式使用过的星星数目和进行研究，找出它们的一般格式，然后将这些格式按星星数目进行分类。他得到下面6个格式：

（1）长格式：每行星星数目长短交错，长的一行星星数比短行的多一个。第一行和最后一行都是长的。（例：50星）

（2）短格式：这个格式与长格式相同，只是第一行和最后一行都是短行。

（3）交错式：这个格式与上两个格式相同，但第一行是长行，最后一行是短行。

（4）等长式：每行的星星数目都相同。（例：48星和49星，49星有些变异）

（5）怀俄明式：第一行和最后一行都是长行，其他的行都是短行。这个名字是因为这个格式是由于怀俄明州的加入而第一次引入的。

（6）俄勒冈式：这个格式与等长格式相同，除了中间一行的星星数目少两个。这个名字是因为这个格式是由于俄勒冈州的加入而第一次引入的。

还有一个没有明示但似乎显然的假定：星星的布局应该是一个长和宽相差不大的矩形。显然把所有的星星都摆在一行里不太美观。于是，假定a是行数，b是长的一行中星星的个数，我们可以合理地让a和b满足：a≤ b ≤ 2a。

历史上，美国国旗的星星排列并不完全是按这6个格式设计的。比如加州加入联邦时的31星旗就很特殊，而按这个分类，它应该是一个短格式。还有一个特殊情况就是当爱荷华州加入联邦时的29颗星，它不能被归到上面任何一种格式中。

给定1 ≤ N ≤ 100，只要N≠ 29，69和87，我们就可以至少给出一个格式来。读者可以试着证明，当N= 29时，上面的6个格式都不能符合要求。不知道为什么美国人没有定义出一个爱荷华式来。

假如我们好奇，用这个程序，当我们考虑像中国的国旗一样有5颗星时它会是怎样分布的呢？下面就是用这个程序选择5颗星所产生的星条旗（如图4）。

图4. 一组不同布局的五星旗

可以看到，威尔逊在程序里设计了好几个方案，唯独没有让一堆小星星围绕一颗大星星。我们前面提到过，最初也确实有过近似这样的设计方案，但坚持平等理念的美国人没有采纳。美国宪法对这些星星的尺寸有严格的规定：如果国旗的高度是1的话，那么每个星星的外切圆的直径是0.0616，即每个红白条的4/5，而每个红白条的宽度是1/13，近似为0.0769。因为美国人认为，每个州都是平等的，每个政党也是平等的，每个人更是平等的，所以小星星不应该有大小不同、颜色区别和位置的特殊性。这些都是威尔逊的程序必须遵守的条件。

3、问题的数学推广

这个问题到这里还没有结束。我们看到，在100以内已经有3个数目是不能由这个程序自动产生星星分布的。那么200以内呢？1千以内，1万以内呢？一般地，当上限充分大的时候会是什么结果呢？伊利诺伊大学厄巴纳-香槟分校的两个研究生考虑了这个问题，并得到了一个有些不可思议的结果：当数目充分大时，能排列好的数目越来越少。具体地说，若S(N)= #{所有能按照上述6种形式之一排列的星星个数n，n≤ N }，则S(50)= 49，S(100)= 97。他们证明了

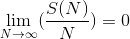
直觉上，我们当然可以想象，当N越来越大时，会出现越来越多的n使得现有的6个格式不能满足需要。上面的怀俄明格式和俄勒冈格式就是因为这个原因加进来的。比较令人意外的是，当N越来越大时，我们要增加的格式会迅速增加。

更令人意想不到的是，这个问题与我们熟知的乘法表有关。数学上的这种关联正是数学的美妙之处。数学家们常常用他山之石来攻破难题。费马大定理的证明就是一个漂亮的例子。鉴于这种思维方法的重要性，我们再稍微说一说上面这个星条旗问题是如何解决的。先来看一看下面的表，这是一个10×10的乘法表（如表1）。

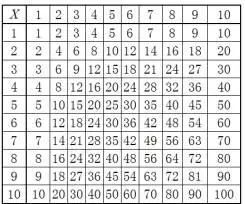
表1

在这个表中有很多重复的数字。我们从上到下一行行看下来，把已经出现过的乘积都删除掉，就得到下面的表（如表2）。（注意这个思想有点像经典的寻找素数的“埃拉托塞尼筛法”。）

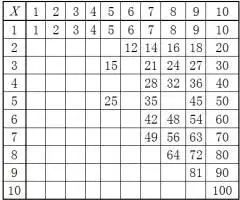
表2

1955年，数学家埃尔特希提出了一个问题：当乘法表充分大时，即当N趋于无穷时，A(N)= #{n ≤ N：n = m₁m_2，m₁ ≤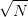，m₂ ≤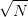}的变化趋势是什么？埃尔特希证明了左上方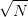×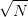的非空白格越来越少：

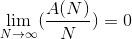
伊利诺伊大学的两位学生就是利用这个结果，经过细致的分析发现S(N)≤ 6∙A(N)，从而结论正确。

最后让我们再回到美国国旗来，看看当N> 50 时他们都准备了什么安排。

图5. 51-55个州时的几个国旗设计

每天好玩的数学

微信号：DailyMathFun

↑

以数学学习为主题，以传播数学文化为己任，以激发学习者学习数学的兴趣为目标，分享有用的数学知识、有趣的数学故事、传奇的数学人物等，为你展现一个有趣、好玩、丰富多彩的数学世界。

↓

点阅读原文逛好玩商城，发现更多好玩的数学。