今天顺着上次的文章(
放假结束该干啥?
)接着说。主要介绍PCA、Kaplan–Meier 生存曲线和ROC曲线。有童鞋提及circos图,这个依凡大大之前有写过,
在windows下安装Circos傻瓜版教程
和
以后不要再说看不懂Circos的图了!
,本文就不多提了。
主成分分析(Principal Component Analysis,PCA)
主成分分析旨在利用降维的思想,把多指标转化为少数几个综合指标,其原理就是将一个高维向量
x
,通过一个特殊的特征向量矩阵
U
,投影到一个低维的向量空间中,表征为一个低维向量
y
,并且仅仅损失了一些次要信息。举个栗子来说吧。下面这个表格是不同样本中基因的表达量,我们可以明显的看出Rasal1、Egfl6和Igf2bp3在不同样本中存在差异,是样本差异的主要成分,并且
Igf2bp3最为明显。那为什么明明是有4个基因,我们直接选出了三个基因来作为样本间差异的指标呢?因为Irf4在各组间表达不存在差异,这个指标直接被忽略了,这样一来,4维的数据就成了3维的数据了。

那如果我们要处理的数据是下面这样杂乱无章的:

我们要进行分析之前就需要对数据进行处理,我们通过
一个特殊的特征向量矩阵对数据进行降维。下图展示了一个三维数据降维到二维平面的过程,简单地说就是找一个最合适的平面,将所有点都投影到这个平面上。
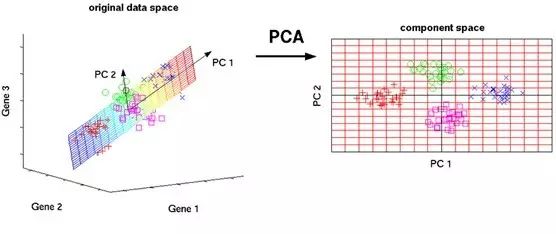
PCA的思想是将n维特征映射到k维上(k
这k维特征称为主成分
。这新的k维特征由原来的k维特征线性组合而成的,是重新构造出来的k维特征,而不是简单地从n维特征中去除其余n-k维特征。为了说明我们重新构造的k维特征(主成分)能够区分两组样本,我们需要检测主成分对数据信息的贡献度(
协方差矩阵计算不同维度之间的协方差
),下图是对筛选出来的20个差异最显著的基因做的PCA分析,结果发现两个主成分对整个数据信息的贡献度很高,表明筛选出来的20个差异基因可以用来明显地区分两组样本。

PCA分析的缺点:
1、在主成分分析中,
我们首先应保证所提取的前几个主成分的累计贡献率达到一个较高的水平
(即变量降维后的信息量须保持在一个较高水平上),
其次对这些被提取的主成分必须都能够给出符合实际背景和意义的解释
(否则主成分将空有信息量而无实际含义)。
2、
主成分的解释其含义一般多少带有点模糊性
,不像原始变量的含义那么清楚、确切,这是变量降维过程中不得不付出的代价。
实现方法:
SPSS、Metlab等。
Kaplan–Meier 生存曲线
在肿瘤研究中,生存曲线是常用的研究药物药效、临床特征以及基因表达情况与疾病预后相关性的工具。
先说生存曲线中的几个概念:
1、事件(Event)
指研究中规定的生存研究的终点。一般指患者的死亡,也可以自定义为疾病的复发、产生耐药等等。
2、生存时间
(
Survival time
)
从检测开始到事件发生所经过的时间。
3、删失(Sensoring)
指由于所关心的事件没有被观测到或者无法观测到,以至于生存时间无法记录的情况。常由两种情况导致:(1)失访;(2)在研究终止时,所关心的事件还未发生。
4、对数秩检测(log-rank test)
对数秩检测有时也被称为
Mantel-Cox测试
,以Nathan Mantel和David Cox命名,其基本思想为:
假定无效假设成立(两总体生存曲线无差别),则根据两种处理不同生存时期的期初观察人数和理论死亡概率计算出的理论死亡数,与实际死亡数应相差不大,否则无效假设不成立,认为两条生存曲线差异有统计学意义
。一般P<0.05有统计学意义,即分组条件的不同与生存具有相关性。在Kaplan-Meier生存分析中有三种检验方法:log-rank、breslow、tarone。log-rank法侧重于远期差别,breslow法侧重于近期差别,tarone法介于两者之间。对于一开始靠得很近,随着时间的推移逐渐拉开的生存曲线,log-rank法较breslow法更容易得到显著性的结果;反之,对于一开始拉的很开,以后逐渐靠近的生存曲线,breslow法较log-rank法更容易获得统计学差异。如果log-rank法有显著差异,而breslow没有差异,可以解释为在开始时生存率没有差异,随之时间的推移生存率出现差异,反之亦然。tarone法是一种折中的方法,介于两者之间。
下面我们来看一张生存分析图,X轴是时间,肿瘤研究一般取5年,Y轴是生存情况,不同颜色的曲线分别代表LINC01555高表达组和低表达组,P<0.001(
log-rank test
结果,表明有统计学意义)

实现方法:
本地工具SPSS、最新版GraphPad等;网络工具
Kaplan Meier Plotter
(http://kmplot.com/analysis/)、
OncoLnc
(http://www.oncolnc.org/)等。
受试者工作特征曲线(Receiver operating characteristic curve,ROC曲线)
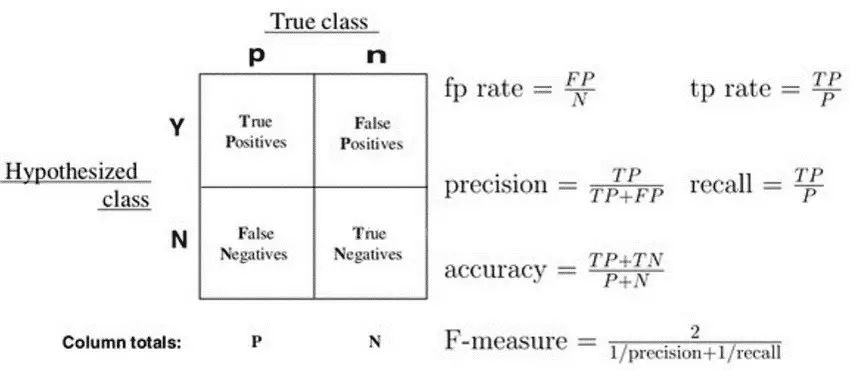
ROC曲线是评价二值分类模型一种图形化方法。要弄懂ROC曲线的含义,首先要搞清楚下面这些概念:
真正(True Positive , TP)被模型预测为正的正样本;
假负(False Negative , FN)被模型预测为负的正样本;
假正(False Positive , FP)被模型预测为正的负样本;
真负(True Negative , TN)被模型预测为负的负样本。
关于这个模型,这里举个栗子,X湿兄、小张、梦熊和机智的怪阿姨这四个人名字中有字母的是坏人,其余是好人,按照这么一个分类模型,X湿兄被归类为坏人,而实际上X湿兄是个好人,所以X湿兄是一个
假负
样本,小张、梦熊和机智的怪阿姨则是
真正
样本。
下面,我们来看一个ROC曲线:
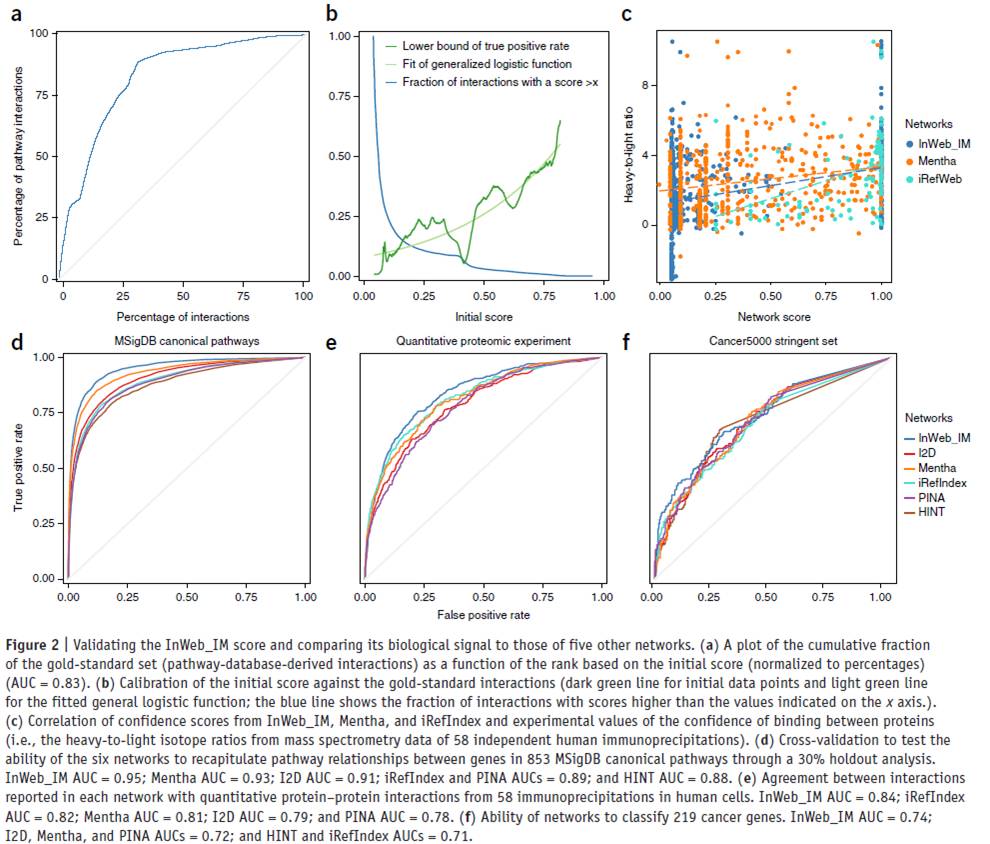
ROC曲线的横坐标为
假正率
(False Positive Rate, FPR或称为特异性
Specificity
),FPR = FP /(FP + TN)(被预测为正的负样本结果数 /负样本实际数),纵坐标为
真正率
(True Positive Rate,FPR或称为灵敏度
Sensitivity
),TPR = TP /(TP + FN)(正样本预测结果数 / 正样本实际数)。
点(0,1):FPR=0, TPR=1. -----> 完美分类器;
点(1,0):FPR=1, TPR=0. -----> 完全错误的分类器;
点(1,1):分类器预测所有的样本都是正例;
点(0,0):分类器预测所有的样本都是负例;
y=x:随机分类器。
一个好的分类模型应该尽可能靠近图形的左上角,而一个随机猜测模型应位于连接点(TPR=0,FPR=0)和(TPR=1,FPR=1)的主对角线上。
ROC曲线下方的面积(Area Underthe ROC Curve, AUC)提供了评价模型平均性能的另一种方法。如果模型是完美的,那么它的AUC = 1,如果模型是个简单的随机猜测模型,那么它的AUC = 0.5,如果一个模型好于另一个,则它的曲线下方面积相对较大。
换句话说
AUC越大
,分类模型越完美,说明分类条件越有意义。
实现方法:
SPSS,Metlab等。
参考文献:
1. Xie, W., et al.,
Identification of transcriptional factorsand key genes in primary osteoporosis by DNA microarray.
Med Sci Monit,2015.
21
: p. 1333-44.
2. Zeng,J.H., et al.,
Comprehensive investigationof a novel differentially expressed lncRNA expression profile signature toassess the survival of patients with colorectal adenocarcinoma.
Oncotarget,2017.
8
(10): p. 16811-16828.
3. Li,T., et al.,
A scored humanprotein-protein interaction network to catalyze genomic interpretation.
NatMethods, 2017.
14
(1): p. 61-64.
长按二维码识别关注“小张聊科研”

关注后获取《科研修炼手册》1.0、2.0、3.0、4.0、基金篇精华合集





