编者按:
前几天发布《五边顶顺风切变》一文后,有位朋友问我:
“为什么五边顶风越大,基准油门越大?”
这个问题一下把我问了个楞憎。
下降率大油门小,下降率小油门大,在我心中一直是天经地义的规则,还真没有认真想过为什么。
坐火车里把铁球扔到装沙子的小滑车上,苍蝇在火车上反方向飞行,从火车上把铁球扔到路边的小车上(也不知道警察怎么想?)......
作为一个中学物理没及过几次格的人,我想了几天试着从两个角度解答这个问题。如果不对的话,还请大家多多指教。
纳粹党徒戈林曾经说过:
“我一听见‘滑块’这个词,就特么忍不住摸腰间的勃朗宁手枪”。


讨论飞机的运动轨迹,我们有两个常用的坐标系,即
“空气坐标系”和“大地坐标系”。
(一)
“空气坐标系”
所谓
“空气坐标系”,是以空气为参照物讨论飞机的运动。作为参照物,空气被视作静止不动的。
严格的讲
“空气坐标系”应当以真空速,而非表速进行分析。但考虑到机场海拔高度远低于巡航高度,且五边的高度差异很小,故而可以视表速为真空速的恒量代换值。
在稳定下降状态,飞机各方向的受力平衡。我们以飞机表速恒定为前提进行讨论。
首先必须澄清一点,飞机的俯仰姿态角度(
ATT
)并不等于飞机实际的下降矢量角度(
FPA
)。
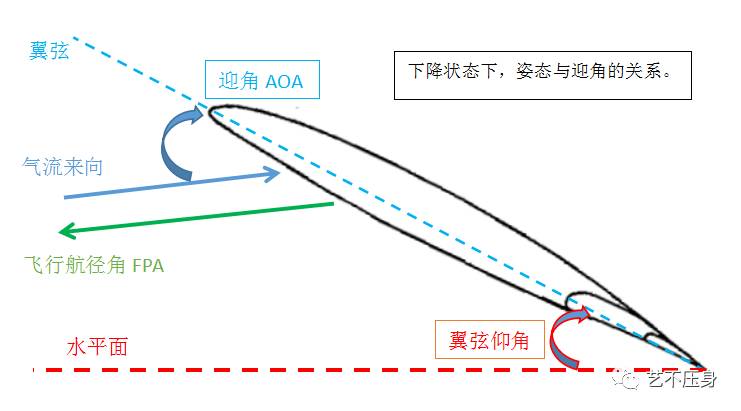
但是在表速恒定,且处于
“
第一速度范围
”的前提下,飞机想要获得更大的下降轨迹角,就必须俯仰姿态角度。二者是正相关的。
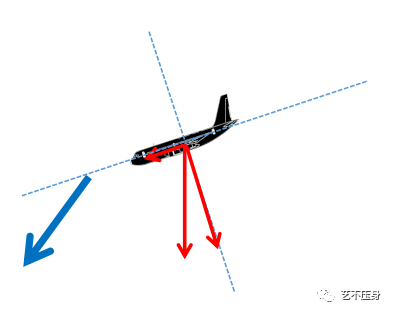
将重力沿飞机纵轴和立轴进行分解。我们可以看出:
(
1
)飞机俯仰姿态越小,重力纵轴分力就越趋向于正推力方向。
(
2
)飞机俯仰姿态越大,重力纵轴分力就越趋向于阻力方向。
这就是说,在受力平衡的前提下,飞机下滑角度越大,所需的推力就越小。
(二)
“大地坐标系”
假定飞机在
“空气坐标系”内以
900ft/min
稳定下降。现在我们将飞机和空气装入一节车厢,让列车沿水平方向运动。
将
“车厢”的水平运动,与飞机的水平运动分量合成,我们即会获得飞机在“大地坐标系”内运动的趋势。(此处假定“车厢”无垂直运动)。
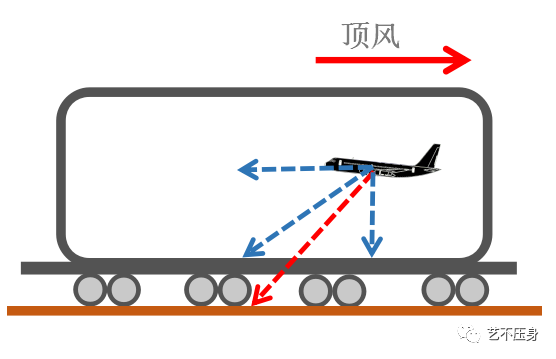
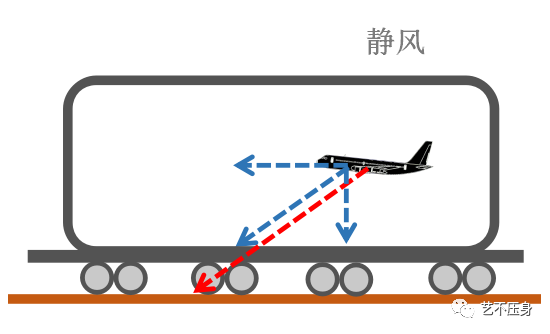
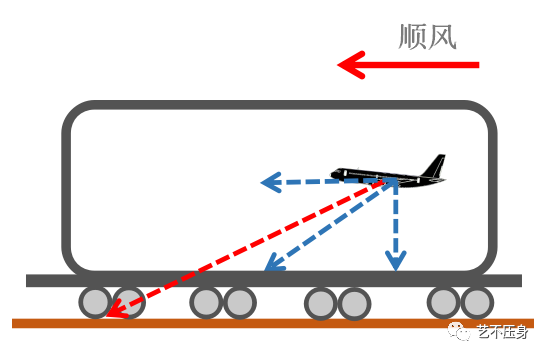
通过上图我们会发现两个问题:
第一,真空速不变的前提下,
“车厢”反向运动越快(顶风越大),地速越小;“车厢”顺向运动越快(顺风越大),地速越大。
第二,下降率不变的前提下,
“车厢运动”(顶顺风)会改变飞机相对于大地的下滑角度。
那么在顶风状态下,如何才能保持与静风相同的3
°
下滑角度呢?
减小下降率,让飞机在
“空气坐标系”中的下滑角小于3
°
。
在上一节我们已经介绍过了,下滑角越小,所需推力越大。
这就是为什么五边顶风的时候,飞机需要更大的推力才能保持下滑线了。当然,顺风同理,效果相反。
(三)单纯使用
“大地坐标系”来分析这个问题
我们也可以单纯借助
“大地坐标系”来分析这个问题。
但这种分析方法,基于三个前提条件:
(
1
)通过几何学分析可知,下滑角度恒定的前提下,地速越小,下降率也越小。
(
2
)表速不变的前提下,顶风越大,地速越小。这个前文已经解释过了。
(
3
)从五边地速基本维持不变。
在稳定大气条件下,高度越低,大气密度越高。维持恒定表速下降,地速会逐渐减小。但是,由于五边高度差很小,所以空气密度引起的地速变化可以忽略不计。
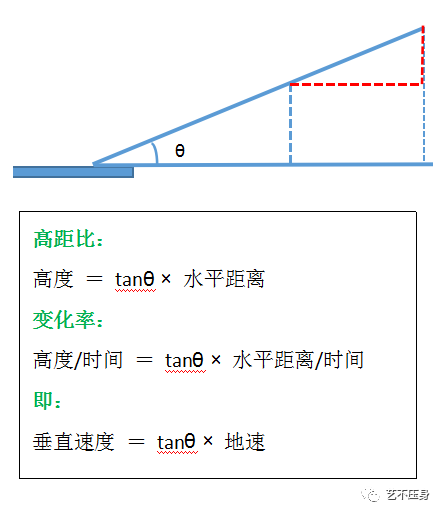
以
“大地坐标系”为视角,在稳定大气条件下,飞机五边地速恒定,高度逐渐降低。
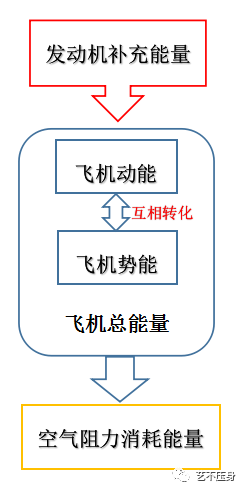
这也就意味着,飞机在动能恒定,势能逐渐减小。
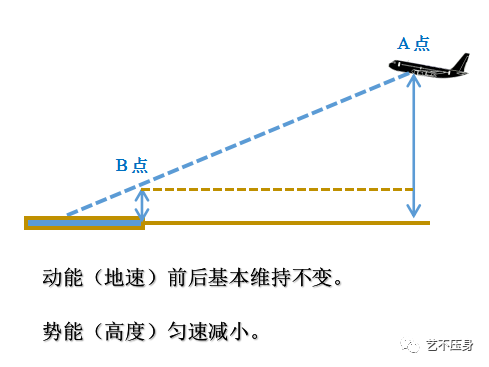
将五边起始下降点(A点),与跑道入口位置(B点)进行比较。
两点间飞机
“总能量”的差值,就是势能的差值。
推力、重力、升力和阻力,共同在五边创造一个
“负功率”状态,
让飞机动能恒定,势能匀速释放
。
那么这个负功率如何计算呢?
“负功率”
=
势能差
÷
时间
不论顶风、静风,还是顺风,AB两点间的势能差是不变的。变化的是释放势能所需的时间。
顶风五边耗时更长。飞机势能释放得更慢。这就意味着,
五边所需的
“负功率”更低
。
那么如何让飞机五边
“负功率”更低呢?
方法只有一个,增大发动机的
“正功率”输出——加油门。