来源：武外英中 周栗
编辑：Gemini
同学们在平常遇到的计算里最头疼的就是根号吧。一般情况下同学们可能看见根号就赶紧拿出计算器。今天我想给大家分享下自己的心得，让大家不再“畏惧”根号，让同学们计算根号时不再需要计算器，甚至不再需要草稿纸。下面的内容分为两大块：如何算根号和如何巧算根号。
如何手动开方？
先告诉大家如何开平方根，我们拿7487267841这个数来举例子，我们先把这个数划分好位数，每两位划分一次，变成74,87,26,78,41，这一共有5段，就代表结果是5位数。我们从左往右算，第一位的计算方法是找一个平方不超过第一段数（74）的最大数（8），于是，
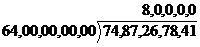，再将得到的平方与原数作差，
然后接下来各位数计算的方法是将已得到的结果乘以2，然后再找一个最大的数，使得这个数加上刚刚的乘积再乘以本身不超过之前的差，再作差，
，
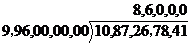(80000*2+6000)*6000=996000000;1087267841-996000000=91267841;
,
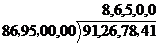(86000*2+500)*500=86950000;91267841-86950000=5017841;
;
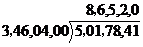(86500*2+20)*20=3460400;5017841-3460400=1557441;
;
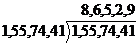(86520*2+9)*9=1557441;1557441-1557441=0;
于是我们得到了结果
，
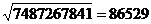你可能会感到有些惊讶，这是为什么，为什么可以这么算根号？其实事实很简单，就是牛顿二项式定理：
(a+b)^2=a^2+2ab+b^2=a^2+(a*2+b)*b,
其中，a是计算中已经得到了的结果：
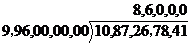的86000，
b是所需求出的下一位数：
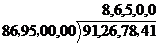中86500的5。
这样对照看来，你是不是明白了？
这时候，有人问到，那可以用这个方法开三次方根吗？四次呢？答案都是可以的，只不过会复杂许多。
，
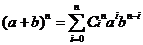当n=3时，(a+b)^3=a^3+3a^2b+3ab^2+b^3，所以如果想开三次方根，我们只要每次找一个最大数b（已得到的结果为a），使得3a^2b+3ab^2+b^3的数值小于之前所得到的差就可以了，不过这次要每三位划分为一段，拿3796416举例，
；
；
；
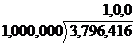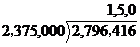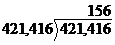于是，
。
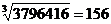以上我是用整数的多次方数来举的例子。大家不妨试试任意数，然后按照保留多少位有效数字的条件来计算，保留几位有效数字就意味着计算几次。这个方法是始终有效的。
如何巧算根号？：误差法。
如果你研究研究怎样巧算，我相信你也会发现这个方法。在误差法里，我们适当的省去数据的位数或是略微修改数据来达到巧算的目的。毋庸置疑，这个方法可以大大提高计算速度。但是在使用的时候要注意精确度。注意这种方法在计算根号很有作用，但是在计算次方时误差会被放大很多倍。
在本周的一节物理课上，老师出了下面这道题：
一个球从10米高的地方落到地面需要几秒？（g=9.81m/s^2，忽略空气阻力）
然后其他同学都纷纷掏出了计算器，我在盘算几秒后发现这道题可以巧算，便随即在草稿纸上写下了1.43。我的同桌表示十分惊讶，问我是怎么算出来的，我坏笑道：“关注我的微信公众号你就知道了。”
事实上，这题用误差法可以很快算出来，下面便是计算的过程：
，
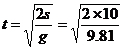其中，
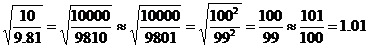
由大家都熟知的
，
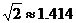我们就可以很快得到
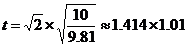
对于1.01这个数，可以运用巧算，
1 4 1 4
+ 1 4 1 4
= 1 4 2 8 2 4=1.42824，
最后保留两位小数得，t=1.43。
如果你按了计算器，你会看到这个结果：1.42784......。
你现在可能在想好神奇，怎么一下就算出来的？也有可能在想，我还没弄懂呢。。。那我就先解释解释吧。
计算这个题的核心就是：
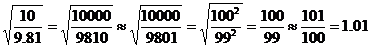
让我把它写的更清楚一些，
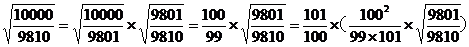
最后一个括号里的数据显然是在1-0.0005和1+0.0002之间的，而根号二在1.4135和1.4145之间的，因此1.01*(1-0.0005)*1.4135
下面我给大家设计了一道例题，请大家尽量不要用草稿纸与计算器：
一列过山车上共有22个座位，当坐满人的过山车和空过山车都以平均速度前进的时候，它们的动能差是111.8kJ，如果人们的平均质量是60kJ，那么过山车的平均速度是多少？（结果保留整数）
