最近老顾访问了很多大学,拜会了很多学术泰斗,同时游历了很多城市,体会了这些城市的独特味道。在烟波浩渺的滇池之滨,空灵秀丽的睡美人山下,老顾与三十年未曾谋面的老同学重逢,也和以前的学生们聚会。印象中的老同学聪慧温润,玉树临风。高中期间酷爱文学诗词,更爱数学物理。最后投笔从戎,进入军校,成为骨科权威。多年来随军驻守在西南边陲,经历了金戈铁马、颠沛流离的军旅生涯。虽然饱经岁月风霜,生活磨砺,老同学性格气质依然如初,从容恬淡,低调柔和,只是话语中隐约透露出杀伐决断的刚毅之气。老同学以昆明特有的牛肝菌、青头菌宴请老顾和老顾的学生们,席间简略地回顾了三十年的人生历程。老同学没有选择医学方面的学术道路,而是选择了直接行医,悬壶济世。主要原因在于学术方面的成果往往要数十年之后才会被社会接受,绝大多数的学术研究终究会融入到整个知识体系之中,被历史的洪流所湮没;临床行医对于社会的贡献更加直接,个人价值的体现更加充分。老同学的一番话语实际上道出了学者内心最深处的恐惧:研究成果被时代所遗忘。年轻学者急于得到社会的承认,饥不择食地选择研究方向,发表论文;成熟的学者多半能够甄破内心的虚荣,审视自己研究结果的真正价值,追求能够超越时代、告慰人生的成果。工程方面的学者很容易赶上时代浪潮,风光一时,但也容易时过境迁,被时代抛弃;基础理论方面的学者往往不被社会理解,一世清贫,但更有机会做出具有恒久价值的成果。老顾觉得老同学挽救过很多人的生命,应该为自己的职业而骄傲。但是老同学却不希望自己的后代从医,因为目前体制原因,医生没有得到社会应有的尊重。他希望老顾为孩子推荐未来依然会蓬勃发展的方向。老顾觉得数学和计算机结合应该潜力无穷。老同学和老顾感慨岁月不饶人,转瞬韶华已逝,暮色将近,他仔细给老顾讲解了腰间盘突出、颈椎老化的内在机理以及防护措施,并且开始憧憬退休之后的幸福生活。老同学在重庆读过研究生,适应了火炉的酷暑之后,娶了重庆太太,对重庆充满了感情,希望近期回到重庆:“重庆有一种独特的味道,深深地吸引着我”。
前不久老顾到重庆探望师兄,在重庆理工听师兄的弟子讲解复几何中的消没定理。重庆整座城市修建在长江两岸的崇山峻岭之上,被无数的穿山隧道和跨江大桥所连接,地势雄奇险峻,水势浩荡汪洋。重庆民风也是彪悍刚烈,热情似火。洪崖洞的吊脚楼风格独特,里面食肆林立,灯影牛肉,张飞火锅,琳琅满目,目不暇给。众食客面色通红,大汗淋漓,痛饮烈酒,爆涮火锅,浓烈辛辣,沸腾喧嚣,一派江湖之气。长江沿岸,专卖麻将机的商铺一字排开,绵延数里,使老顾觉得这里的生活果然从容闲适,悠然自得。但是朝天门码头摩天大厦拔地而起,其气度几乎不输上海陆家嘴,特别是长江边上有两幢高楼,通体黄金打造,金灿灿、夺人双目,明晃晃、气势逼人,使人觉得川蜀的传统生活方式受到了现代节奏的威胁。
在现代文化浪潮冲击下,能够坚持自身的文化传统的城市非苏州莫属。对于北方人而言,江南是一个神秘的文化符号,那里有小桥流水人家,那里有青石板铺就的雨巷,会走出打着油纸伞、丁香般结着愁怨的姑娘。苏州无疑是典型的江南城市,极富文艺气息。江南的梅雨季节,天空晦暗迷蒙,苏州的建筑却是白墙黑瓦,对比鲜明。建筑格局宛若一幅水墨国画,线条简约,大片留白,错落有致,素雅沉静。整个城市无时不刻不沉浸在香樟的隐约香气之中,间或有桂花糕的味道飘来。苏州的平江街传承自唐宋,沿着一条蜿蜒的小河而建,河上各色拱桥,小巧精致,两侧粉墙黛瓦,古意盎然。很多古宅都被改成临街店铺,极有韵味,堪称是文艺青年的人间天堂。与商业逐利相比,这里商家的理想是“贩卖美好”(一家商铺的名字),你只需“撒娇”就可以议价(另一商铺的提示)。在这里,你能够回忆起久被遗忘的童年,体会到各种文艺情愫,观赏到各种文化创意。老顾重温了上个世纪80年代的小人书,给20年后的自己写了明信片,买到了活版印刷的铅字,欣赏了美轮美奂的玉雕,看到了苏绣的绝活。有一种双面绣的技艺冠绝天下,背面绣亭台楼榭,正面看笼罩着烟雨迷蒙,然后再从正面绣上才子佳人,如此前景背景相互映衬,相得益彰。满街都是充满江南特色的小吃,酒酿丸子、鲜肉月饼、海棠糕、竹筒糍粑,名字听起来就很风雅。但也听说“鸡脚旮旯”(一家店名)的鸡脚也很不错,只因名字粗俗,所以隐藏在旮旯里。华灯初上,老顾在临河的“姑苏菜馆”中体会苏州菜,点了著名的太湖三白,由太湖中的三种河鲜烹饪而成,细腻而鲜美;沽了一壶糯米黄酒,柔和而温热。河道上,小船穿梭来往,船娘头戴斗笠、身着蓝青花短衫,一边摇橹一边唱着船谣。河畔,身着汉服的少女婷婷袅袅,沿街徜徉。夜幕中隐约传来苏州评弹,春莺百转,醉心荡魄。河水倒映着阑珊夜色,静流无声,吴都千年,古韵悠然。
苏州丰厚的文化底蕴,宛如氤氲的香气,渗透到生活的所有细节。老顾在老苏州茶馆早餐,点了一道招牌菜:三虾面。老顾被这道面的精致所震撼,但见面条细如发丝,太湖虾仁晶莹剔透,虾头火红如琥珀,虾籽灿若星芒。在没有机械的古代,将细小透明的太湖虾分解成虾仁和虾头,这得需要多么灵巧的双手和多大的耐心?一碗面的食材需要耗费多少时间才能准备齐全?老顾的很多英国、德国的朋友对于中国饮食文化觉得难以理喻,原因在于他们觉得没有必要为食物的烹饪花费太多的时间和精力。老顾却觉得欧美文化没有发明出筷子,无法用刀叉灵活地剔除鱼刺,因此他们只能食用厚实少刺的海鱼,无法享用细腻多刺的淡水鱼,缺少了很多人生乐趣。老茶馆的建筑和陈设都是承袭古制,酸枝桌椅,雕花门窗,竹制灯笼,红木中堂。门口一只青花大瓷缸,内养荷花锦鲤。整体感觉非常和谐典雅,简约舒适。老顾对着雕花门窗找了半天黄金分割率,也没找到。看来东西方的美学标准的确不同,美学价值观念也各有千秋,不必一以贯之。
老顾慕名观赏了名闻天下的苏州拙政园,这里的园林艺术登峰造极。奇峰怪石,崇楼幽洞,荷塘鱼池,名葩奇木,处处都是优美的景致。园内亭台楼榭错落有致,玲珑古雅,飞檐斗拱,雕梁画栋。“卅六鸳鸯榭”、“十八曼陀罗花馆”,名字优雅,令人浮想联翩,“与谁同坐轩”更令人无论如何也想不到清风明月。这里的怪石造型追求瘦露透皱,具有复杂的拓扑和曲率。这里的雕花窗棂讲究移步换景,绝不雷同。老顾仔细研究了雕花的几何模式,发现各种平面对称性都被巧妙应用,特别是现代雕花从平面模式进化到了纽结结构。但是现代几何的双曲对称性还没有出现在这些木雕艺术之中。设想一位古代江南才子,每天经过“桃花渡”,穿越“竹香廊”,登上“啸月台”,梳风延月,诵读诗书,何等逍遥。同样,一位现代江南才子,依然可以在醇酽的文化氛围中思考黎曼度量、亚纯微分、曲率联络,其美学体验一脉相承。双曲几何的出现使人类意识到欧氏几何并不是天然的真实几何,这是古典几何和现代几何的分水岭。
在深圳,老顾拜会了机械设计、计算力学与机器人研究领域的国际知名学者,香港科技大学的王煜教授,王教授是水平集结构拓扑优化方法的主要创始人。王教授对于高亏格度量曲面容许双曲结构这一理论非常有兴趣,他对于共形几何在机械设计和计算力学领域的应用前景非常看好。对于老顾团队应用黎曼面理论来为网格生成奠定理论基础,王教授给与了充分肯定。王教授认为机械领域的几何表示主要有设计领域的样条NURBS,分析仿真领域的不规则四面体网格剖分,规则四边形和六面体剖分是联结这两种基本表示的桥梁。
在上一讲中,我们证明了曲面四边形网格和亚纯四次微分的等价性,从而用阿贝尔定理给出网格奇异点构型的条件。阿贝尔定理是说黎曼面上亚纯微分的除子经过阿贝尔-雅可比映射,映到雅可比簇的零点。雅可比定理推广了阿贝尔定理。雅可比定理给出了黎曼面Picard群和雅可比簇为加群同构。
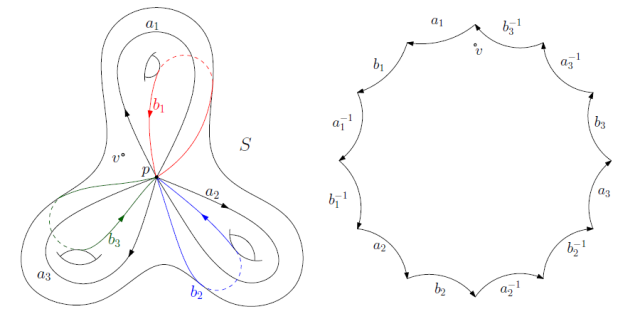
图1. 典范基本群基底和基本域。
我们下面用较为严密的数学语言来解释四边形网格奇异点构型的条件。假设M是一个亏格为g的封闭曲面,嵌入在三维欧氏空间之中,因而具有欧氏度量诱导的度量
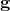 。我们选取曲面的典范基本群基底
。我们选取曲面的典范基本群基底
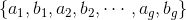 ,
,
满足条件:
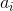 和
和
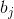 的代数相交数为
的代数相交数为
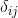 ,
,
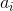 和
和
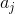 ,
,
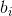 和
和
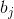 的代数相交数都为0。我们将黎曼面沿着基本群典范基底切开,得到一个基本域。度量曲面
的代数相交数都为0。我们将黎曼面沿着基本群典范基底切开,得到一个基本域。度量曲面
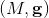 同时为黎曼面,假设其全纯微分群的基底为
同时为黎曼面,假设其全纯微分群的基底为
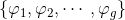 ,
,
由此我们构造所谓的周期矩阵
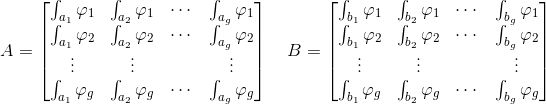
如此得到
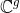 中的格点群
中的格点群
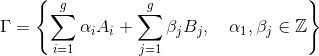 ,
,
这里
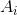 是A周期矩阵的列向量,
是A周期矩阵的列向量,
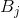 是B周期矩阵的列向量,
是B周期矩阵的列向量,
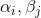 都是整数。商空间
都是整数。商空间
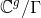 被称为是黎曼面
被称为是黎曼面
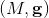 的
雅可比簇
的
雅可比簇
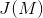 。根据Torelli的工作,雅可比簇可以反过来决定黎曼面。
。根据Torelli的工作,雅可比簇可以反过来决定黎曼面。
从黎曼面到雅可比簇的
Abel-Jacobi映射
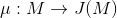 被定义为:
被定义为:
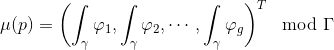
这里
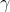 是定义在基本域中,联结某个固定基点
是定义在基本域中,联结某个固定基点
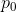 和
和
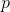 的一条路径。
的一条路径。
引理
:设
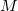 是亏格为g的紧致黎曼面,
是亏格为g的紧致黎曼面,
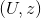 为
为
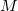 的一个局部坐标系,则存在U中g个不同的点
的一个局部坐标系,则存在U中g个不同的点
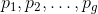 ,及一组全纯微分的基底
,及一组全纯微分的基底
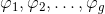 , 使得矩阵
, 使得矩阵
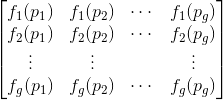
为非退化的,其中全纯微分的局部表示为
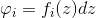 。
。
先取
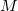 上的非零全纯微分
上的非零全纯微分
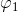 , 其在U中不能恒为零,因此存在一点
, 其在U中不能恒为零,因此存在一点
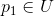 ,使得
,使得
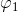 在此点处非零。由于
在此点处非零。由于
 ,我们可以在
,我们可以在
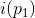 中取全纯微分
中取全纯微分
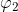 , 使得
, 使得
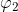 在某点
在某点
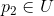 处非零。又由
处非零。又由
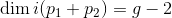 ,我们可以在
,我们可以在
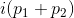 处取全纯微分
处取全纯微分
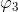 ,使得
,使得
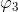 在某点
在某点
 处非零。如法炮制,我们就得到g个点
处非零。如法炮制,我们就得到g个点
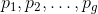 及g个非零全纯微分
及g个非零全纯微分
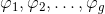 ,使得
,使得

如果在U内
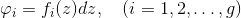
则g阶方阵
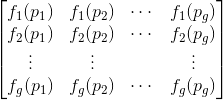
为下三角矩阵,且对角线元素非零,因而为非退化的矩阵。同时
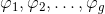 为一组全纯微分基底。证明完毕。
为一组全纯微分基底。证明完毕。
现在设
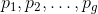 是这个引理中的g个点,我们定义一个新的映射如下:设乘积流形
是这个引理中的g个点,我们定义一个新的映射如下:设乘积流形
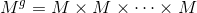 ,定义
,定义
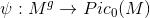 ,
,
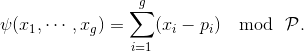
定理
(Jacobi定理)映射
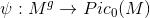 为满射,
为满射,
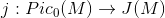
为加群同构,因而
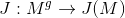
也是满射。
证明:设
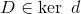 是次数为零的除子,考虑次数为g的除子
是次数为零的除子,考虑次数为g的除子
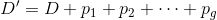
由Riemann-Roch公式,有
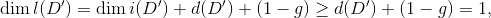
因此存在非零亚纯函数
 ,此时
,此时
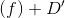 的次数为g,因此可以写成
的次数为g,因此可以写成

这意味着
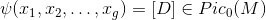 , 即
, 即
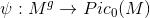 为满射。
为满射。
根据Abel定理,
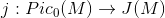 为单射。由于
为单射。由于
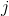 为加群同态,为了说明
为加群同态,为了说明
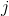 为同构,只要证明
为同构,只要证明
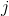 的像包含
的像包含
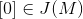 的一个开邻域即可。我们只需证明,
的一个开邻域即可。我们只需证明,
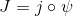 的像包含这样的一个开邻域。
的像包含这样的一个开邻域。














