在科技历史上,数学为工程技术提供了理论基础、指引了未来发展方向;反过来,工程技术为数学提出了新的挑战,推动了数学理论的发展。深度学习和最优传输理论再度验证了这一历史发展模式。
深度学习在工程技术领域取得了巨大的成功,其内在原因在于自然数据集具有内在的规律:流形分布定律,即一类自然数据可以被视为嵌入在高维背景空间中的低维数据流形上的一个概率分布。深度学习算法可以被解耦为学习流形结构和学习概率分布。在深度学习算法中,流形结构被表示为编码映射和解码映射,即数据流形的局部参数化;概率分布可以被表示成吉布斯势能函数,或者最优传输映射。最优传输映射将白噪声(高斯或者均匀分布)映射成数据分布。所有的映射,编码、解码、传输映射等都被深度神经网络来逼近。
由几何逼近理论,我们从离散采样点集合来重建数据流形,目的是保证重建流形与初始数据流形一致。这里,所谓一致具有不同层面的含义,通常由弱到强指拓扑结构,Hausdorff距离,黎曼度量和微分算子的一致性,需要不同的采样要求。例如曲率高的区域、内射半径小的区域、数据分布密度高的区域需要更加稠密的采样。由此可见,为了训练深度学习模型,我们需要数据流形上的稠密采样点,并且采样点的分布忠实地反映了真实数据分布规律。因此,我们需要大量训练数据。
但是,很多大数据与个人隐私相关,具有强烈的敏感性,无法直接公开提供给社会各界使用,这成为未来深度学习的社会学方面的瓶颈。生成模型是突破瓶颈、实现数据脱敏的一种强有力的技术方法。例如,人脸图像数据集会泄露人脸信息,侵犯个人隐私;但是对于深度学习人脸识别算法,我们由需要大量人脸图像用于训练和提高模型性能。这时我们可以应用生成模型来生成大量的人脸图片,这些图片看上去与真人无异,但是现实生活中并不存在,因此不会侵犯任何人的隐私,同时也可以帮助人脸识别模型提高性能。

图0. 生成的人脸图像不具备社会学意义,同时反映了真实数据的统计特性。
这种方法的理论诠释如下:假如我们确切掌握了数据流形的信息和数据的分布,我们用数论方法产生伪随机变量满足均匀分布,用最优传输映射和解码映射变换成数据流形上的随机变量,满足数据分布,如此得到生成采样,即为生成的人脸图片。由几何测度理论,数据流形为连续统,训练数据集为离散点集,因此生成采样落在训练数据集的概率为零。(在实际算法中,也可以加上限制以避免生成采样落在训练集内)即便编码、解码映射与最优传输映射完全公开,用户由生成人脸图片可以回溯到计算机生成的随机数,但是这个随机数没有任何社会学意义,均匀分布的信息熵最大,信息泄露最少。
同时,这种方法保持了数据集的统计特性,生成数据集符合真正数据分布,因此对于基于统计特性的实际应用而言,生成数据完美地解答了他们所关心的问题。例如,一家服装设计公司,他们需要各种人体形状在人群中的分布情况,以决定各种尺码服装的生产比例。这种信息可以通过统计生成数据来计算出来。由此可见,依随人们日益重视数据安全和隐私保护,生成模型的应用会更加广泛和深入。
深度学习的一个主要算法瓶颈是所谓的模式坍塌(模式崩溃 mode collapse)问题,具体表现为模型对于超参数过于敏感,训练收敛困难,误差长期震荡;如果数据分布具有多个模式,生成数据会丢失一些模式,或者生成数据会覆盖所有模式,但是同时生成模式之外的失真数据。
模式坍塌的内在原因可以分析如下:深度学习中所有的映射都用深度神经网络来逼近,但是深度网络只能表达连续映射;但是概率分布之间的传输变换有可能是非连续变换。这一本质矛盾导致了模式坍塌。那么是在什么情形下,最优传输映射是非连续的呢?这需要由最优传输映射正则性理论来回答。虽然最优传输理论已经发展了两百多年,传统的数学家们只关心连续的最优传输映射,对于非连续的奇异集合没有太多研究,因此最优传输映射奇异集合理论一直处于尚未深入探索的阶段。深度学习的兴起,将会燃起数学家们巨大的热情,这一领域的发展将会迎来一次飞跃。
最优传输理论
我们回忆一下经典的最优传输理论。
给定分布
定义在开集
上,和分布
在
上,满足平衡条件
。
映射
被称为是保测度的,如果对一切Borel集合
,都有
。
给定传输代价函数
, 蒙日问题在所有保测度映射中寻找传输总代价最小者,
蒙日问题的解被称为是最优传输映射。
Brenier理论表明,在较为一般的情形下,存在定义在
上的凸函数
,被称为是 Brenier势能函数,其梯度映射给出了最优传输映射,
。由保测度条件
,我们可以得到Monge-Ampere方程, 假设密度函数为
并且
, 我们有
满足边界条件
。
图1. 如果源区域和目标区域都是凸集,密度函数光滑,则Brenier势能光滑。
经典的Monge-Ampere方程正则性理论都假设
和
是凸集合,例如密度函数满足光滑性条件
,
,这时Brenier势能函数
,最优传输映射光滑,不存在奇异集合。如图1所示,
和
都是单位圆盘,Brenier势能函数光滑,最优传输映射连续,不存在奇异集合。
图2. 如果目标区域非凸,则最优传输映射非连续,Brenier势能非光滑。
如图2所示,我们计算从单位圆盘
上的均匀分布到海马区域
上的分布区域之间的最优传输映射(
下行
),则Brenier势能函数(上行)全局连续,但是沿着红色曲线不可微分。在单位圆盘上,红色曲线的投影是黑色的曲线,被称为是奇异集合,最优传输映射在奇异集合上间断。因此,传输映射是非连续映射。如果目标区域
接近凸集,那么有可能最优传输映射依然是连续的。
一个自然的问题在于:奇异集合存在的充分必要条件是什么?这个问题的解答与深度学习中的模式坍塌具有本质联系。这里我们用区域
边界的曲率给出一个充分条件,即所谓的“
遛狗
”定理。
如图3左帧所示,
假设有一位朋友遛狗,这位朋友在平面上的轨迹是一条封闭曲线
,狗的轨迹是另外一条封闭曲线
,人和狗都是逆时针行走,在任意时刻,在各自轨道上一直面向前方,从不回头(但是走过一圈,整体上绕回到起点)。
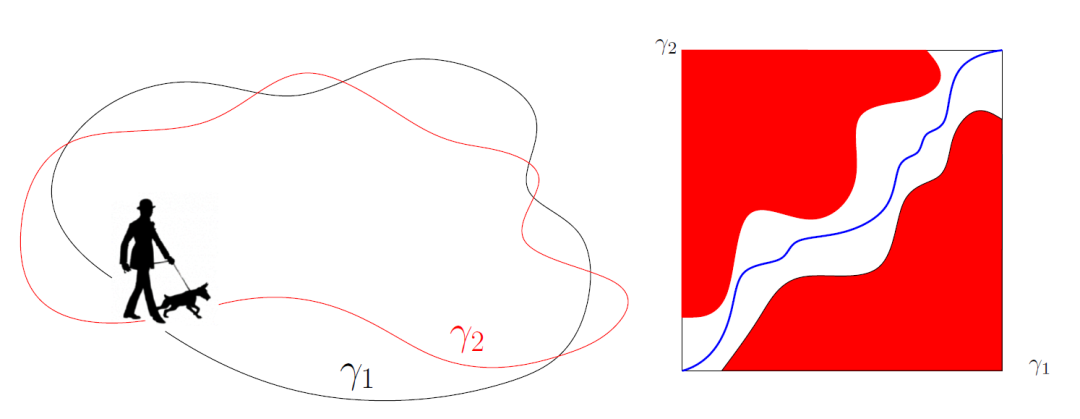
图3. 在各种遛狗方式中,最短的牵狗绳长度等于曲线间的Frechet距离。
Frechet 距离
同一时刻人和狗的位置之间有个对应关系,这自然给出了轨道间的一个同胚映射
,等价的我们用参数来表示
。由人和狗都不回头的假定,我们自然有
对于任意时刻
都成立。那么不同的遛狗方式对应着不同的同胚映射
。如果固定一个遛狗方式
,牵狗绳的长度不小于人和狗之间任意时刻的最大距离
。在所有可能的遛狗方式中,最短的牵狗绳长度等于
我们将
可能
的
最短牵狗绳长度定义为
和
的Frechet距离。
在计算几何中,人们对于Frechet距离的算法已经有了充分的研究。如图3右帧所示,我们用横轴表示
的参数
,纵轴表示
的参数。任何同胚映射
,满足
可以表示成一条连接对角点的曲线,曲线在水平和铅直两个方向都是单调的。给定一个
,对于正方形内任意一点
,如果
,我们将其绘为红色,反之为白色。那么白色区域为自由区域,红色区域为禁止区域。如果白色区域中存在一条水平、铅直都单调的曲线,连接对角点,则这两条曲线的Frechet距离小于
。实际计算中,我们可以用二分法来搜索
,找到
的Frechet距离。
法向Frechet距离
类似的,假如
和
的正则性较好,例如它们是
光滑的,则沿着曲线法向量是良定义的。由此我们可以定义法向Frechet距离:我们将人和狗所在位置之间的距离换成人和狗所在点处的外法向量之间的距离,写成公式就是
这里
是单位圆上的测地距离。
倾斜条件
给定平面区域间的最优传输映射,边界曲线
和
是二阶光滑的,
满足一定的光滑性条件,那么最优传输映射可以拓展到边界上,
,并且满足所谓的倾斜性条件(Obliqueness Condition),即给定边界上一点
,
即边界点的法向量和对应像点的法向量夹角小于等于直角。
遛狗定理
假设已知
定义在平面区域上
概率分布,
和
,这里概率密度函数满足比较宽泛的正则性条件,边界曲线
和
是二阶光滑;如果
和
的法向Frechet距离大于
,则最优传输映射非连续,存在奇异集合。
假如最优传输映射
不存在奇异集合,Brenier势能函数全局可微,那么
可以拓展到边界上,并且在边界上的限制
是同胚,并且满足倾斜条件,因此
和
的法向Frechet距离不大于直角,矛盾。于是我们得出结论:存在奇异集合,最优传输映射在奇异集合上间断。
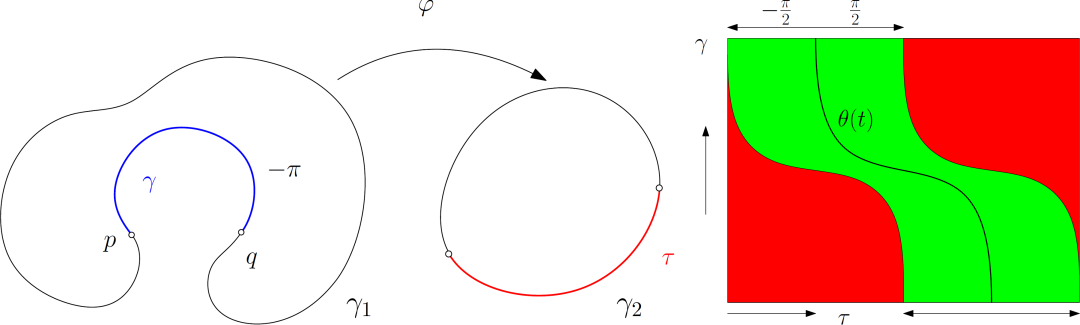
图4. 奇异集合存在的曲率条件。
曲率条件
由遛狗定理,我们可以给出一些最优传输映射存在奇异点的曲率条件。如图4左帧所示,如果
有一段曲线,总曲率小于















