概率论要解决的问题
概率论是很古老的数学分支了——探讨的是不确定的问题,就是说,一件事情可能发生,也可能不发生。然后,我们要预计一下,它有多大机会会发生,这是概率论要解决的问题。这里面要特别强调概率和统计的区别,事实上这个区别在很多文章里面被混淆了。举一个简单的例子,比如抛硬币。那么我们可以做两件事情:
1.我们预先知道抛硬币的过程是“平衡的”,也就是说出现正面的机会和出现背面的机会都是50%,那么,这就是我们的概率模型——这个简单的模型有个名字——伯努利试验(Bernoulli trial)。然后,我们可以预测,如果我们抛10000次硬币,那么正面和背面出现的次数大概各在5000次左右。这种执因“测”果的问题是概率论要解决的,它在事情发生之前进行。
2.我们预先不知道抛硬币的过程遵循什么法则。于是,我们先去做个实验,抛10000次硬币,数一下正面和反面各出现了多少次。如果各出现了5000次,那么我们可以有很高的信心去认为,这是一个“平衡的”硬币。如果正面出现9000次,反面出现1000次,那么我们就可以基本认为这个硬币遵循一个严重偏向正面的非平衡法则——正面出现的概率是10%。这种执果溯因的事情是统计要解决的,它在事情发生之后进行,根据观察到的情况归纳背后的模型(Model)或者法则(Law)。

这篇文章只讨论概率论的问题。
经典概率的困难
什么是概率呢?长期以来,一个传统而直到今天还被广泛运用的概念是:概率就是一个事情发生的机会——这就是经典概率论的出发点和基础。大部门的初等概率论教科书,给出一个貌似颇为严谨的定义:我们有一个样本空间(sample space),然后这个样本空间中任何一个子集叫做事件(event),我们给每个事件A赋一个非负实数P(A)。如果P(A)满足
那么我们就称P为概率。这个定义,以及由此而演绎出来的整个经典概率体系,广为接受并被成功用在无数的地方。
但是,这样的定义藏着一个隐蔽很深的漏洞——使得从这个定义出发能在数学上严格导出互相矛盾的结果。假设样本空间是S=[0, 1],里面的实数依循均匀分布,我们构造这样一个集合。首先,建立一个等价关系:
相差值是有理数的实数是等价的。
依据这个等价关系,把0到1之间的实数划分为等价类,这样我们有无数个等价类。从每个等价类中随便抽出一个实数作为代表,这些代表构成一个集合,记为H。(注意:我们有不可数无限个等价类,因此这个集合的存在依赖于选择公理(Axiom of Choice))
那么P(H) 是什么呢?
如果P(H)等于零,那么P(S) = 0;如果P(H) > 0,那么P(S) = 无穷大。无论如何,都和P(S) = 1的要求矛盾
。这下麻烦大了,我们一直依赖的概率定义竟然是自相矛盾的!
也许,从数学家的眼光看来,这个问题很严重。但是,这对于我们有什么意义呢。我们一辈子都用不着这种只存在于数学思辨中的特殊构造的集合!不过,即使我们从实用出发不顾及这类逻辑漏洞,传统概率论还是会给我们带来一定程度的麻烦。
一个问题,可能大家都有所感觉。那就是,我们在本科学习的概率论中有着两套系统:
离散分布和连续分布
,基本什么定理都得提供这两种形式,但是它们的推导过程似乎没什么太大差别,一个用求和一个用积分而已。几乎一样的事情,为什么要干两遍呢。
离散分布
还有,那种离散和连续混合的分布又怎么处理呢?这种“离散连续混合的分布”不仅仅是一种理论可能,在实际上它的应用也在不断增长。一个重要的例子就是狄里克莱过程(Dirichlet Process)——它是learning中的无限混合模型的核心——这种模型用于解决传统有限混合模型中(比如GMM)子模型个数不确定的难题。这种过程,在开始时(t = 0)通常是连续分布, 随着时间演化,在t > 0时变成连续和离散混合分布,而且离散部分比例不断加重,最后(几乎必然)收敛到一个离散分布。这种模型用传统的连续和离散分离的处理方式就显得很不方便了。
事实上,我们是可以把对连续模型,离散模型,以及各种既不连续也不离散的模型,使用一种统一的表达。这就是现代概率论采取的方式。
现代概率论——从测度开始
现代概率论是前苏联大数学家Kolmogorov在上世纪30年代基于测度理论(Measure theory)的基础上重新建立的,它是一个非常严密的公理化体系。什么是测度呢?说白了,就是一个东西的大小。测度是非负的,而且符合可数可加性,比如几块不相交的区域的总面积,等于各自面积之和。这个属性和概率的属性如出一辙。测度理论自从勒贝格(Lebesgue)那个时候开始,已经建立了一套严格的数学体系。因此,现代概率论不需要把前辈的路子重新走一遍。基于测度论,概率的定义可以直接给出:
概率就是总测度(整个样本空间的测度)为1的测度。
测度理论和经典概率论有个很大的不同,不是什么集合都有一个测度的。比如前面构造的那个奇怪的集合,它就没有测度。所以,根据测度理论,样本空间中的集合分成两种:可测的(measurable)和不可测的。我们只对可测集赋予测度或者概率。特别留意,
测度为零的集合也是可测的,叫做零测集。
所谓不可测集,就是那种测度既不是零,也不是非零,就是什么都不能是的集合。
因此,根据测度理论,我们描述一个概率空间,需要三个要素:
一个样本空间,所有可测集
(它们构成sigma-代数:可测集的交集,并集和补集都是可测的),
还有就是一个概率函数,给每个可测集赋一个概率。
通过引入可测性的概念,那种给我们带来麻烦的集合被排除在外了。不过,可测性的用处远不仅仅是用于对付那些“麻烦集合”。它还表达了一个概率空间能传达什么样的信息。这里暂时不深入这个问题,以后要有机会写到条件概率(conditional probability)和鞅论(Martingale theory)时,再去讨论这个事情。这里只是强调一下(虽然有点空口说白话),可测性是讨论随机过程和随机分析的非常重要的概念,在实际计算和推导中也非常有用。
我们看到,这套理论首先通过可测性解决了逻辑上的漏洞。那怎么它又是怎么统一连续和离散的表达的呢?这里面,测度理论提供了一个重要的工具——
勒贝格积分(Lebesgue Integral)。
噢,原来是积分,那不也是关于连续的么。不过,这里的勒贝格积分和在大学微积分课里面学的传统的积分(也叫黎曼积分)不太一样,它对离散和连续通吃,还能处理既不离散又不连续,或者处处有定义而又处处不连续的各种各样的东西)。
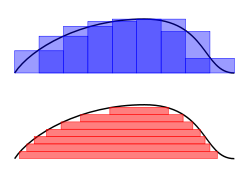
勒贝格积分
举一个简单例子,比如定义在[0, 1]的函数,它在[0, 0.5)取值为1,在[0.5, 1]取值为2。这是一个简单的阶梯函数,期望是1.5。按照传统的黎曼积分求期望,就是把定义域[0, 1]分成很多小段,然后把每小段加起来。勒贝格积分反其道而行之,它不分定义域,而是去分值域,然后看看每个值对应的那块的面积(测度)是多大。这个函数取值只有两个:1和2。那么值为1那块的面积为0.5, 值为2的那块的面积也是0.5,积分就是以这些值为系数,把对应的面积加起来:0.5 x 1 + 0.5 x 2 = 1.5。
上面是连续的情况,离散的呢?假设我们在一个离散集[0, 1, 2]上定义一个概率,P(0) = 0.5, P(1) = P(2) = 0.25。对一个函数f(x) = x,求均值。那么,我们看到,值为0, 1, 2对应的测度分别是0.5, 0.25, 0.25,那么我们按照“面积加权法”可以求出:0 x 0.5 + 1 x 0.25 + 2 x 0.25 = 0.75。
对于取值范围连续的情况,它通过取值有限的阶梯函数逼近,求取上极限来获得积分值。
总体来说,勒贝格积分的idea很简单:
划分值域,面积加权
。不过却有效解决了连续离散的表达的统一问题。大家如果去翻翻基于测度理论建立起来的现代概率论的书,就会看到:所谓“离散分布”和“连续分布”的划分已经退出历史舞台,所有定理都只有一个版本——按照勒贝格积分形式给出的版本。对于传统的离散和连续分布的区别,就是归结为它们的测度函数的具体定义不同的区别。















