微信昵称为“一生何求”的读者朋友问到了下面的问题:
左老师好,下面这道题是2016年新课标2卷的文科导数大题第2小问,我用的是分离参数法,可以做出来.图片中的是原版答案,用的是分类讨论.

我的疑问是:
如何确定分类讨论的标准?怎么想到a<=2?
希望左老师百忙之中能够抽出时间给予指导.

一生何求,
的确,这个讨论的标准好像魔术师手里的帽子,太神奇,太突然.
我们来一起思考:第2小问讨论的目的是什么?
......思考1分钟.

所以,问题的本质上是研究二次函数在区间上的零点分布.这就回到我们熟悉的轨道上来.
二次函数是高中阶段研究的最为透彻、最为深入的函数.它的两个核心问题——
-
二次函数在闭区间上的最值问题;
-
二次函数在区间上的零点分布问题.
务必熟练掌握,做到解题的任何时候都能信手拈来.
把导函数f'(x)构造成一个新函数,专门研究它在(1,+∞)的零点分布问题.
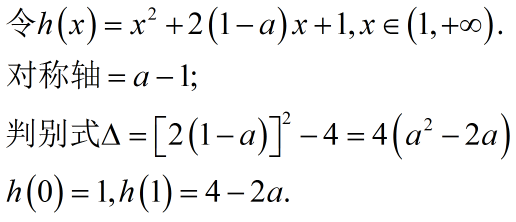
大家能够看到,我捎带着研究了
对称轴、判别式、特殊点以及端点的函数值
.因为这些因素会最终影响到零点的有无以及个数.
f'(x)即h(x)在
(1,+∞)上无零点或者有不变号零点的情况
下面画出h(x)在(1,+∞)上无零点或者有不变号零点的图示,并求解出对应的a的取值范围.
情况1:
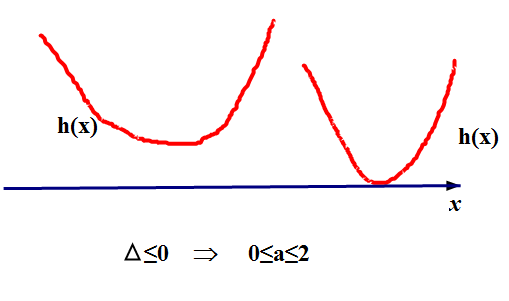
情况2:
情况1和情况2求并集知,当a≦2时,导函数f'(x)
在(1,+∞)上无零点或者有不变号零点,即导函数
f'(x)
非负,故原函数在(1,+∞)上单调递增.
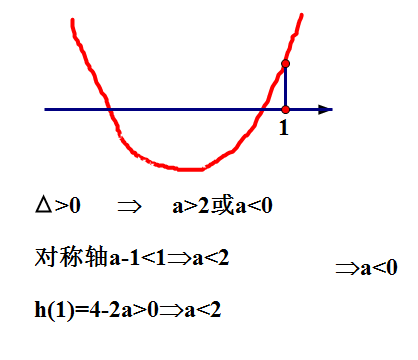
f'(x)即h(x)在(1,+∞)有变号零点的情况
下面画出h(x)在
(1,+∞)上有变号零点的图示,并求解出对应的a的取值范围.
情况3:
在
(1,+∞)上有1个变号零点.
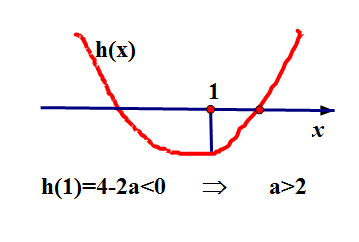
情况4:
在
(1,+∞)上有2个变号零点.
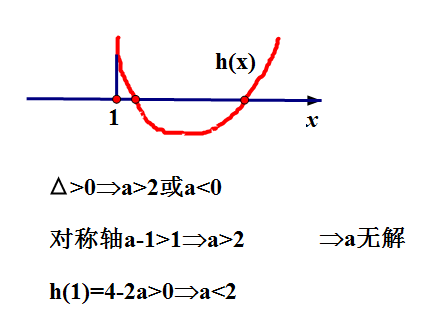
情况3和情况4求并集知,当a>2时,导函数f'(x)在
(1,+∞)上有变号零点,即原函数f(x)在
(1,+∞)上不单调,有极值.
评价
从以上1、2部分的分析,我们能看出,“a是否大于2”决定了“函数f(x)在(1,+∞)上是否单调”,所以2成为了讨论的标准.
但是,重点听但是.
在真实的考场上,如果你这样分析,恐怕再给你2小时,你也答不完.
所以,能分离参数当然要分离参数.
要把分离参数法放在首发的位置
.
当然,你也可以练习简化讨论的方法.
至于如何简化讨论,以后有空再写.
祝开心.
温馨提示
:要获取微信公众号“高考数学左老师”的精华内容,可以
回复“关键词”,你会获得一份关键词列表.根据这份列表,回复对应的关键词,就可获得内容.
推荐阅读:
圆锥曲线定点问题2
上一篇:
三角形面积秒杀法
--END--
苹果手机用户专属赞赏二维码






