机器学习与优化
引用大佬Pedro Domingos的说法:机器学习其实就是由
模型的表示,优化和模型评估
三部分组成。将一个实际问题转化为待求解的模型,利用优化算法求解模型,利用验证或测试数据评估模型,循环这三个步骤直到得到满意的模型。
因此,优化算法在机器学习中起着一个承上启下的作用!
一般机器学习中涉及的优化命题可以表示为:
比如:
还有等等等等机器学习算法也是类似的。
优化算法基础
优化算法的阶次
所谓优化算法的阶次其实指的是优化过程利用的是
-
-
-
中的哪些信息。
如果函数形式未知、梯度难以求或不存在的时候常常采用零阶优化算法;在机器学习领域中一般一阶算法使用较多,二阶算法可能收敛更快但计算花费也更大。
优化算法的常见组成
在理解梯度下降法之前, 再给大家复习一下几个非常容易混淆的概念: 导数是一元函数的变化率 (斜率)。如果是多元函数呢? 则为偏导数。偏导数是多元函数 “退化"成一元函数时的导数, 这里 "退化"的意思是固定其他变量的值, 只保留一个变量, 依次保留每个变量, 则
元函数有
个偏导数。如果是方向不是沿着坐标轴方向, 而是任意方向呢? 则为方向导数。换句话说, 偏导数为坐标轴方向上的方向导数, 其他方向的方向导数为偏导数的合成。而偏导数构成的向量就称为梯度。
梯度方向是函数增长速度最快的方向, 那么梯度的反方向就是函数减小最快的方向。因此, 如果想要计算函数的最小值, 就可以用梯度下降的思想来做。假设目标函数的梯度为
, 当前点的位置为
, 则下一个点的选择与当前点的位置和它的梯度相关
其中
为学习率, 可以随着每次迭代改变。(就拓展出了许多相关的算法AdaGrad、RMSProp、Adam等)
当目标函数存在不可微部分, 常会采用近端梯度下降法。比如
, 其中
是凸的且可微,
是凸的但是不可微或者局部不可微。由于
不可微, 我们不能直接用梯度下降法来寻优(PS:次梯度算法可以, 就是慢了点), 因此近端算法考虑的是将
进行近端映射。
函数
的近端映射可以定义为
拿个机器学习中常见的
范数给大家举个例子,
(一范数就是各元素 绝对值之和),对应的近端映射表示为
这个优化问题是可分解的! 也就是对每一个维度求最小值
对
的正负进行分类讨论, 然后利用一阶最优条件(求导令导数为零)可得
这通常也被称作软阈值(soft thresholding)。
因此近端梯度算法也就是
在求解一个优化命题时,如果其对偶形式便于求解,常常可以通过求解对偶问题来避免直接对原问题进行求解。比如机器学习中典型的SVM就涉及到对偶理论,以及拉格朗日乘子法、KKT条件等概念。首先简单通俗地说说这几个概念是干嘛的
-
对偶理论:对偶也就是孪生双胞胎,一个优化命题也就有其对应的兄弟优化命题。
-
拉格朗日函数:将原本优化命题的目标函数和约束整合成一个函数。
-
如果原问题是凸问题,则KKT条件为充要条件,也就是说满足KKT条件的点也就是原问题和对偶问题的最优解,那就能够在满足KKT条件下用求解对偶问题来替代求解原问题。
(具体推导和细节就不展开了,下次可以单独写一篇)
当遇到大规模问题时, 如果使用梯度下降法(批量梯度下降法), 那么每次迭代过程中都要对
个样本进行求梯度, 所以开销非常大, 随机梯度下降的思想就是随机采样一个样本来更新参数, 那么计算开销就从
下降到
。
无约束问题的典型算法
上面提到过了就不重复了。
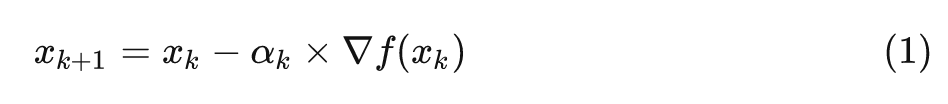
梯度下降法可能存在的一个问题是为了收敛到解附近,
同样的迭代方向可能走了不止一次(导致收敛慢)
。共轭梯度就可以理解为选择一系列线性无关的方向去求得最优解。因此共轭梯度法把共轭性与最速下降方法相结合,利用已知点处的梯度构造一组共轭方向,并沿这组方向进行搜素,求出目标函数的极小点。
方向的构造方法为:
其中当初始化的时候相当于梯度下降法(因为初始时刻只有梯度方向)。这里末知项是这个系数
, 它的计算公式为
有了搜索方向,那么每次次迭代为

在说拟牛顿法前先简单介绍一下牛顿法,牛顿法最初是为了求解方程的根而推导出来的公式。它的主要思想是
基于当前位置的切线
来确定下一次的位置。比如要求
的解,可以迭代求解

如果对应到求解优化命题, 我们要使得
取最小值, 也就是函数的一阶导数为零
, 带入牛顿法求根公式就是
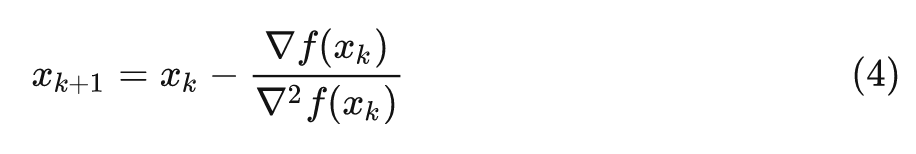
由于牛顿法每次都要计算二阶导数(Hessian矩阵)的逆,计算量太大了,因此有了拟牛顿法。简单的说,拟牛顿法其实就是
用近似Hessian矩阵来进行迭代
。
比如说令















