机器之心编译
选自:Google Research Blog
参与:李泽南、路雪
昨天,谷歌发布了 TensorFlow 1.4.0 先行版,将 tf.data 等功能加入了 API。同时发布的还有 TensorFlow Lattice,这家公司希望通过新的工具让开发者们的模型更加准确。
机器学习已经在很多领域取得了巨大成功,如自然语言处理、计算机视觉和推荐系统,它们都利用了高度灵活的模型捕捉复杂的输入/输出关系。然而,我们还面临着语义输入与全局关系之间的问题,像「如果路上堵车,开车通勤的时间就会变长,其他方式也是一样。」一些灵活的模型如 DNN 和随机森林无法学习这种关系,可能会无法泛化至不同样本分布的样本。
针对这种问题,谷歌提出了 TensorFlow Lattice,它包含一套易于使用的预制 TensorFlow 估算器,以及 TensorFlow 运算符(operator),可用于构建你的点阵模型。Lattice 是多维度内插值查找表-,类似于几何教科书中近似正弦函数的查找表-。通过查找表结构,我们可以通过键入多个输入来逼近任意灵活的关系,以满足你指定的单调函数关系来让泛化更好。这意味着,查找表中的值可以最小化训练样本的损失,但是,查找表中的相邻值被约束以沿着输入空间的给定方向增加,这让模型在这些方向上的输出也有所增加。重要的是,由于它们在查找表值之间插值,所以 Lattice 模型是平滑的,预测也是有界的,这有助于在测试时间内避免失真的过大或过小预测。
假设你正在设计一个向用户推荐临近咖啡厅的系统。你肯定需要模型学会「如果两家咖啡厅是连锁的,推荐更近的一家。」下图展示了准确地与部分东京用户(紫色)训练数据匹配的灵活模型(粉色)示例,在那个城市有很多咖啡厅。粉色灵活模型对有噪声的训练样本有些过拟合,与「更近的咖啡厅更好」的原则不符。如果你使用这个模型在德州(蓝色)找咖啡厅,你会发现它的行为有些奇怪,有些时候甚至会向你推荐更远的咖啡厅!
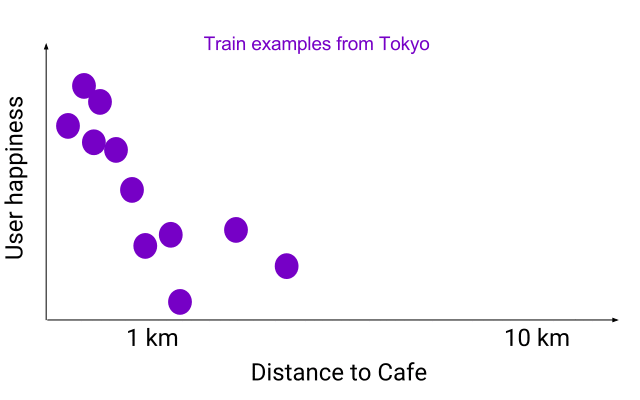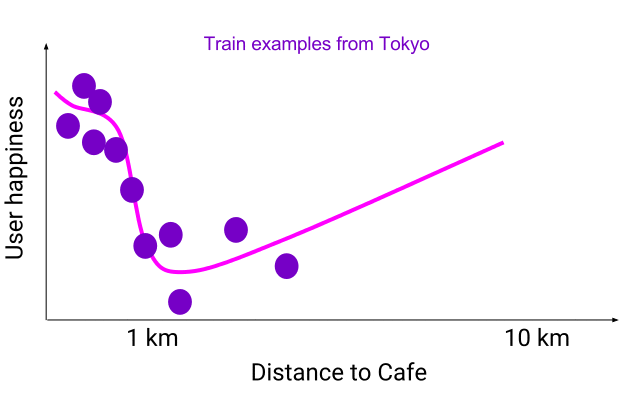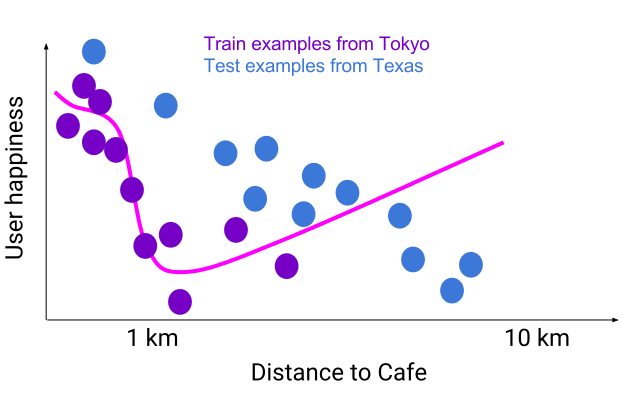
模型的特征空间——所有其他输入保持一致,只有距离产生变化。一个与东京训练样本(紫色)准确拟合的灵活函数(粉色)预测 10 公里外的咖啡厅要比 5 公里外同样的咖啡厅更好。如果数据分布产生变化,这个问题还会变的更加明显,正如德州数据(蓝色)所展示的那样。
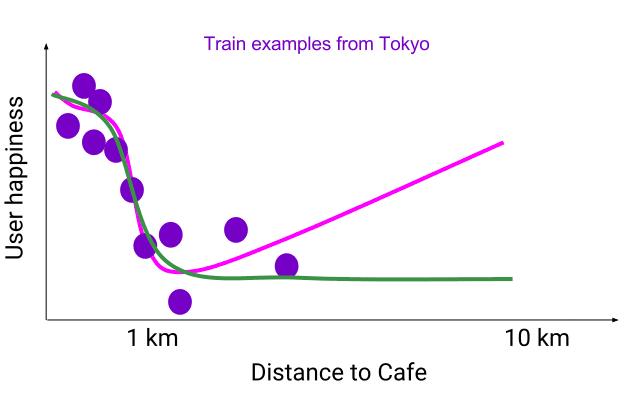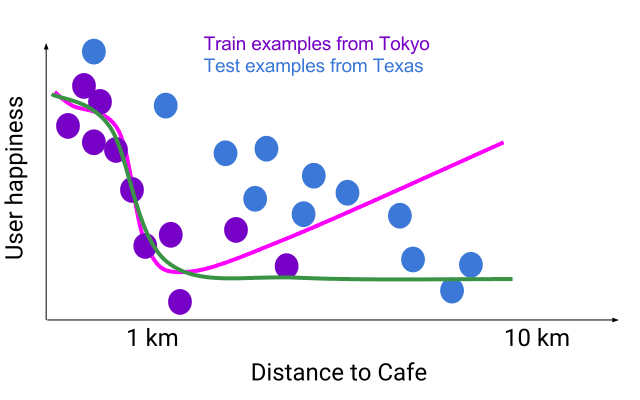
单调灵活函数(绿色)在训练样本上结果准确,也可以泛化到德州样本,相比非单调灵活函数(粉色)效果更好。
相比之下,同样使用东京样本训练的 lattice 模型可以接受约束,以满足这样的单调关系,得出一个单调灵活函数(monotonic flexible function,绿色)。绿线还能够准确拟合东京的训练样本,且很好地泛化到德州数据,不优先选择较远的咖啡厅。
通常,对于每个咖啡厅你可能有很多输入,如咖啡质量、价格等。灵活模型捕捉全局关系较为困难,「如果所有输入是一样的,那么越近越好。」尤其是训练数据的部分特征空间稀疏且有噪声。能够获取先验知识(如输入对预测的影响)的机器学习模型在实践中效果较好,且易于调试、具备更强的可解释性。
预制 TensorFlow 估算器
谷歌提供了多个 lattice 模型架构,如 TensorFlow 估算器。其中最简单的估算器是校准线性模型(calibrated linear model),它学习每个特征的最优 1-d 转换(使用 1-d lattice),然后把所有校准后的特征进行线性连接。在训练数据集非常小或没有复杂的非线性输入交互的情况下,这种模型表现很好。另一种估算器是校准 Lattice 模型(calibrated lattice model)。该模型使用两层的单个 Lattice 模型将校准后的特征进行非线性连接,可以展现数据集中的复杂非线性交互。校准 Lattice 模型通常适合 2-10 个特征的情况,如果有 10 个或更多特征,我们认为使用校准 Lattice 的集合可以帮你获取最佳结果,你可以使用预制 Ensemble 架构进行训练。单调 Lattice 集合比随机森林达到 0.3% - 0.5% 的增益精度 [4],与之前使用单调性的顶尖学习模型相比,这些新型 TensorFlow Lattice 估算器达到 0.1 - 0.4% 的增益精度 [5]。
构建你自己的模型
你或许想使用更深层的 Lattice 网络进行实验,或使用局部单调函数(partial monotonic function)作为深度神经网络或其他 TensorFlow 架构的一部分。我们提供预构建模块:用于校准器的 TensorFlow 运算符、Lattice 内插和单调投影(monotonicity projection)。例如,下图展示了一个 9 层的深度 Lattice 网络 [5]。
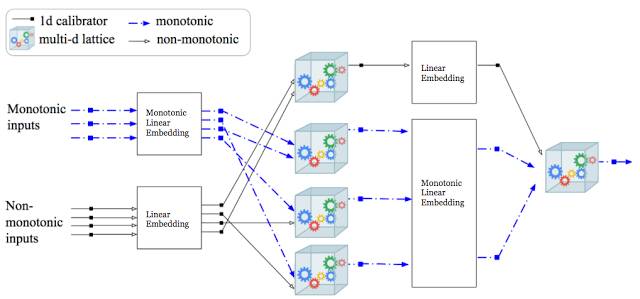
9 层深度 lattice 网络架构 [5]、线性嵌入的交互层,以及带有校准器层的 Lattice 集合(类似神经网络中的多个 ReLU)的示例。蓝线代表单调性输入,该输入逐层保存,进而为整个模型服务。该架构和其他随机架构都可以使用 TensorFlow Lattice 构建,因为每一层都是可微的。
除了模型灵活性和标准 L1 和 L2 正则化之外,谷歌还提供使用 TensorFlow Lattice 的新型正则器:
基于输入(如上所述)的单调性约束(Monotonicity constraint)。
Lattice 上的拉普拉斯正则化,使学得的函数更加平坦。
Torsion 正则化,控制不必要的非线性特征交互。
谷歌希望 TensorFlow Lattic 能够对处理有意义的语义输入的大型社区有所帮助。同时,开发团队还在致力于研究可解释性、控制机器学习模型以满足策略目标、使从业者利用他们的先验知识,这是其中的一部分。我们很高兴能够与大家分享。查看我们的 GitHub 和教程(https://github.com/tensorflow/lattice/blob/master/g3doc/tutorial/index.md),开始使用吧。
参考文献
[1] Lattice Regression (https://papers.nips.cc/paper/3694-lattice-regression), Eric Garcia, Maya Gupta, Advances in Neural Information Processing Systems (NIPS), 2009
[2] Optimized Regression for Efficient Function Evaluation (http://ieeexplore.ieee.org/document/6203580/), Eric Garcia, Raman Arora, Maya R. Gupta, IEEE Transactions on Image Processing, 2012
[3] Monotonic Calibrated Interpolated Look-Up Tables (http://jmlr.org/papers/v17/15-243.html), Maya Gupta, Andrew Cotter, Jan Pfeifer, Konstantin Voevodski, Kevin Canini, Alexander Mangylov, Wojciech Moczydlowski, Alexander van Esbroeck, Journal of Machine Learning Research (JMLR), 2016
[4] Fast and Flexible Monotonic Functions with Ensembles of Lattices (https://papers.nips.cc/paper/6377-fast-and-flexible-monotonic-functions-with-ensembles-of-lattices), Mahdi Milani Fard, Kevin Canini, Andrew Cotter, Jan Pfeifer, Maya Gupta, Advances in Neural Information Processing Systems (NIPS), 2016
[5] Deep Lattice Networks and Partial Monotonic Functions (https://research.google.com/pubs/pub46327.html), Seungil You, David Ding, Kevin Canini, Jan Pfeifer, Maya R. Gupta, Advances in Neural Information Processing Systems (NIPS), 2017
原文链接:https://research.googleblog.com/2017/10/tensorflow-lattice-flexibility.html
本文为机器之心编译,转载请联系本公众号获得授权。
✄------------------------------------------------
加入机器之心(全职记者/实习生):[email protected]
投稿或寻求报道:[email protected]
广告&商务合作:[email protected]
















