“机器学习”这个词怎么近两年在哪哪哪都能见到,一会预测股市走向,一会预测机票价格,一会跟病理医生PK识别癌症病理切片,一会去下围棋,一会去打电竞。但总是不明白那到底是什么鬼,耳熟不能详。
但我还是强烈感觉到,它将来一定会对医学产生很大的影响,除了听说过的“某AI在某病的诊断上又超过了医学专家”之外,它的研究方法也会引入医学科研中,提高我们做科研的效率,并可能开发出很多有意思的成果。
这不,最近发在Lancet Neurology上的一篇文章,为帕金森病的认知损伤开发一个简单易用的风险评分量表,即在已报道过的风险因素中筛选出有较大影响力的几个,建立预测模型。它就是在传统方法的基础上加入了一点机器学习的方法,没有太深太复杂,恰好能带我们一窥其风采(入坑向导←_←)。

1.帕金森病中的认知损伤还没有有效的干预手段;
2.那是因为相应的临床研究中,还有没办法对认知功能进行有效的基线控制和预测,导致临床研究的效率不高;
3.瞧瞧隔壁心血管科,人家有个Framingham风险评分,就是基于简单的性别、年龄及其他心血管危险因素,来预测10年内心血管疾病发生率,炒鸡friendly。我们帕金森也要搞一个。
首先,
研究者收集汇总了9个已发表研究的纵向队列数据(北美+欧洲),有的是人群观察队列,有的是生物标志物研究队列,有的是临床试验队列。它们原来的实验设计、纳排标准、和评价指标都不同。研究者认为正因此,由这些数据开发出为的模型更具有普适性。
9个队列的患者数据经过一系列纳排标准的筛选后,又把剩下的分为两个库,一个是由6个队列组成的发现库(discovery population),用于建立模型;另一个是重复库(replication population),由3个队列组成,用于验证模型。
其次,
建模所需要的风险因素(即自变量,Predictors),也是从既往文献报道中整理出来的,共有9个,分别为:
简易精神状态量表(MMSE);
蒙特利尔认知评估量表(MoCA);
国际帕金森病运动障碍协会改良统一帕金森病评分量表第II、第III部分(MDS-UPDRSII、MDS-UPDRS III);
帕金森病的发病年龄;
受教育年限;
性别;
抑郁状态;
β-葡糖脑苷脂酶(GBA)基因突变。
以上就是研究所需要的材料。然后通过那9个队列的数据,对9个变量进一步筛选,找出哪些确实有影响力,哪些没有;有影响力的,影响力又有多大,这才能形成一个精致的评分模型。
整个研究的流程如Figure 1所示:
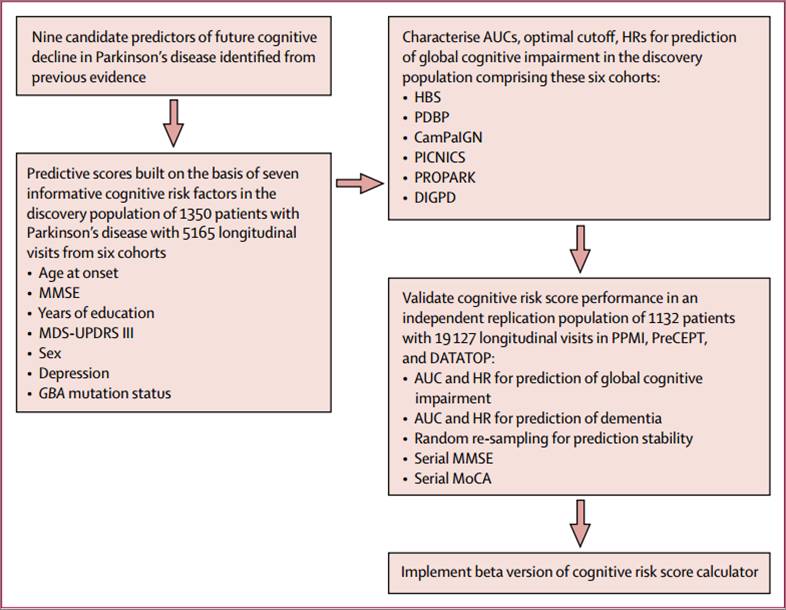
Figure1实验设计
第一步:建立模型
先在发现库中用Cox回归计算每个自变量的回归系数、风险比(HR)等统计量,剔除无效的自变量,于是MDS-UPDRSII评分先被刷掉了。
剩下的8个风险因素则进入一个多变量Cox模型,用后消除法剔除无显著性的变量,于是又剔除了Hoehn-Yahr分级。
剩下的7个风险因素和它们的回归系数一起构成了认知风险评分系统,即发病年龄、基线MMSE、受教育年限、基线MDS UPDRS-III评分、性别、基线抑郁状态和GBA突变。
用这个评分系统来预测患者帕金森发病10年内是否会出现整体认知功能损伤,有很高的准确率,AUC为0.86,在风险评分0.196的临界点上,特异性为0.72,敏感性0.87(Figure 2A)。
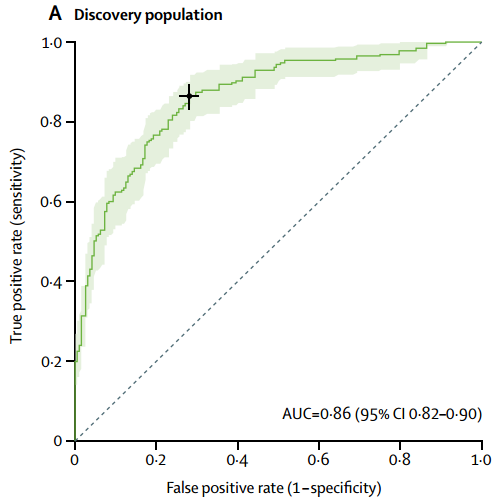
Figure 2A 发现库的认知风险评分ROC曲线
接下来,研究者提取评分处于最高四分位数和最低四分位数的患者数据,形成两个分组,绘制K-M曲线(Figure 2C)。发现最高四分位数的患者,HR比最低四分位数者高。处于最低四分位数的患者有95%能安稳度过10年而不发生认知损伤,而最高四分位数者只有34.9%能幸免。
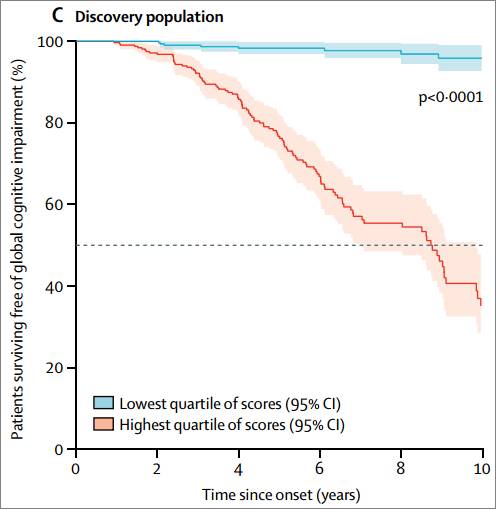
Figure 2C 发现库中评分最高和最低四分位数的认知损伤K-M曲线
第二步:验证模型的预测效力
将刚才开发出来的预测模型,放到新的样本(重复库)中,模拟预测其10年的整体认知损伤发生概率,绘制ROC曲线(Figure 2B)。结果AUC为0.85,在0.196的临界点上,特异性0.74,敏感性0.73。
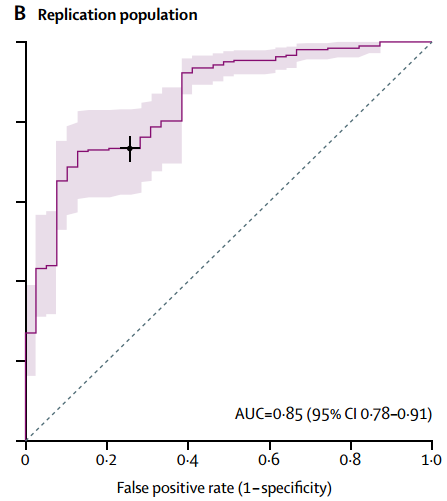
Figure 2B重复库的认知风险评分ROC曲线(纵坐标接Figure 2A)
四分位数分组情况相似,也绘制K-M曲线(Figure 2D)。风险评分处于最低四分位数者,10年内有96.3%的患者幸免于整体认知损伤,评分处于最高四分位数者,只有27.4%幸免。
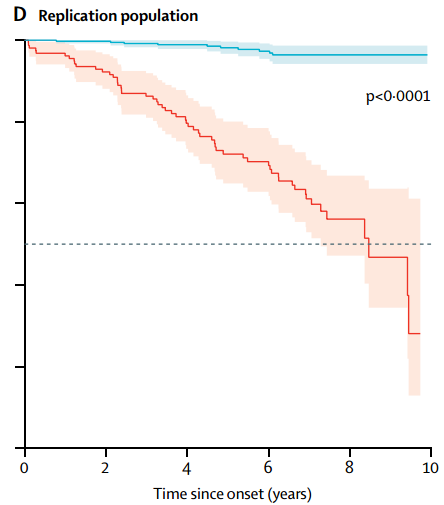
Figure 2D 重复库中评分最高和最低四分位数的认知损伤K-M曲线(纵坐标接Figure 2B)
再用来预测10年内帕金森病痴呆(PDD)的发生率,其AUC比预测整体认知损伤还要略高一些,达到0.88。在0.196分的临界点上,敏感性0.86,特异性0.72。最高四分位数的患者只有48.3%幸免于痴呆,最低四分位数有98.9%能幸免(Figure 3)。
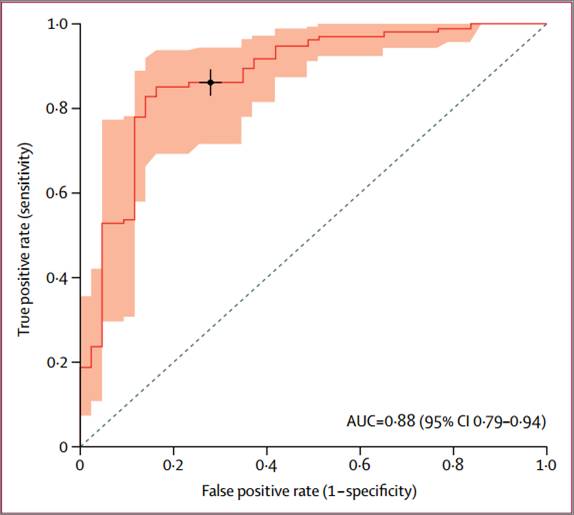
Figure 3 在重复库中预测10年内PPD的发生率
第三步:检验模型的稳定性
传统的研究做到上面两步也就够了,可以宣布这个模型测试良好,接着拿去申请下一次研究的经费,测试实际应用啥的。但本研究就是在这里异峰突起,加入了机器学习中用得较多的bootstrap方法。
对bootstrap简单理解就是,从整体中有放回地重复取样(resample)N次,一般N>1000,得到N个子集,每个子集样本量都一样。然后用这些子集计算我们需要的统计量T(在本案例中,T就代表预测认知风险的评分模型,然后计算其AUC),这样我们就得到了N个T,然后通过计算T的均值、方差、分布等特征,去评估它的准确性和稳定性。
本研究中N=10000次。每次新抽取的样本都分为训练集(training set)和测试集(test set),分别对应发现库和重复库。重新在训练集中建立预测模型,重新在测试集中进行验证。
10000次迭代运算后,原模型中的发病年龄、基线MMSE、受教育年限这3个自变量,在每次迭代的新模型中都保留了;基线MDS-UPDRS III评分在98.30%的模型中留下,GBA突变有91.79%,抑郁状况90.61%,性别78.52%。而原来被剔除的Hoehn-Yahr分级,则在34.86%的迭代中被加入了模型中(Figure 4A)。可以看出,纳入原模型的7个自变量是稳定的,而Hoehn-Yahr分级则有点小波动,但仍可以忽略。
把这10000次训练集生成的新模型用到各自对应的测试集中进行预测,其中预测10年内发生整体认知损伤的平均AUC为0.83,预测PDD的则达到0.87,这与之前的自变量筛选、预测性能测试的结果相一致。Figure 4B即为10000次迭代中预测认知损伤和痴呆的AUC分布情况,显然是正态分布。
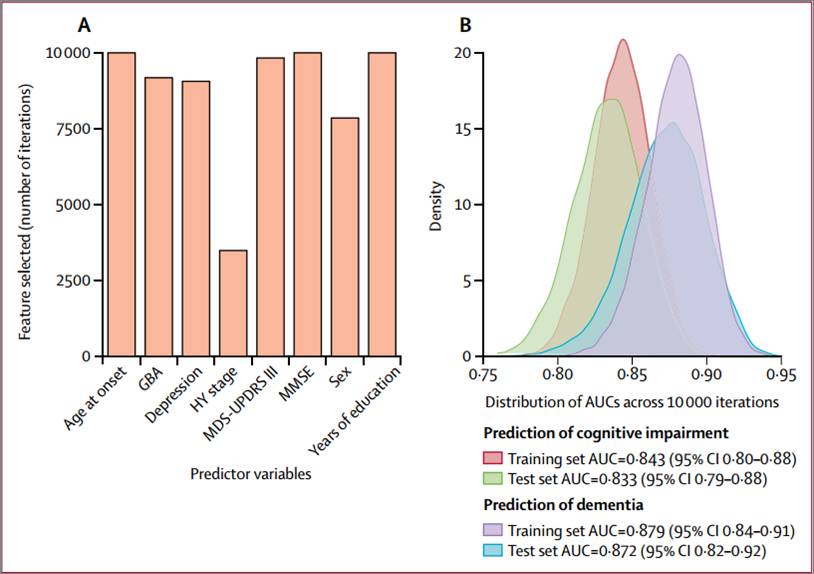
Figure 4 评分模型的稳定性
第四步:模拟应用
本研究的目的不就是为临床研究提供控制基线的工具么,所以模拟一下临床试验的场景。假设有一个为期3年的临床试验,研究某药物延缓或逆转PD认知功能损伤的疗效。
认知功能损伤的量化指标通常都是MMSE量表或MoCA量表,所以先看一下重复库中风险评分和这两个量表的关系,发现基线风险评分高者,后来的MMSE就降得越快,MoCA也有相似的模式。这说明在临床试验中以CRS > 0.196为纳入标准,能成功富集高风险的受试者。
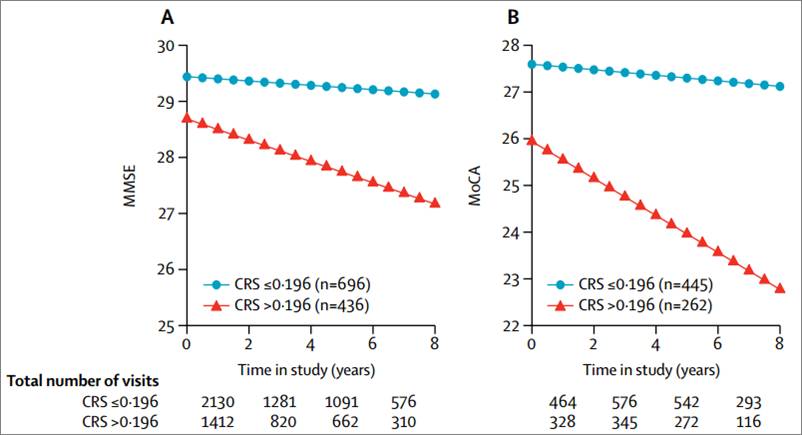
Figure 5A&B 风险评分分组与MMSE及MoCA变化轨迹的关系
接下来,一个临床研究好坏的评价指标之一是统计功效(power),要达到80%才算好。那么为了达到80%的功效,要纳入多少样本才够呢?
我们知道统计功效跟效应量和样本量都是呈正相关,二者越高,统计功效越高。如果以评分>0.196来控制入组基线,组间差异的效应量就能提高。于是在统计功效一定的情况下,就能减少所需要的样本量。
经过计算,用MoCA作为量化指标时,干预组和对照组各137人就可以达到80%的统计功效,而MMSE没有MoCA那么敏感,需要各组152人。但如果不加控制,则MoCA需要每组801人,MMSE需要每组802人,差了大约6倍。所以应用该评分是不是大大节省了科研资源?
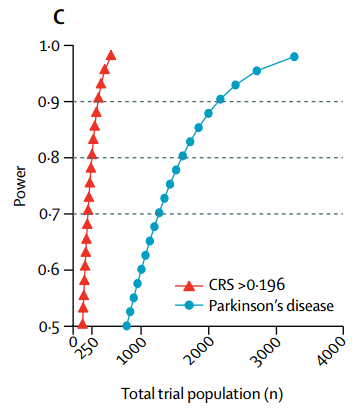
Figure 5C 高风险评分和普通受试者样本量与功效的关系
至此,其实该模型的预测效力、稳定性及应用前景都得到了很好的探讨,但作者又做了一些锦上添花的善后工作。















