
介绍
这篇教程适用于有兴趣将贝叶斯方法应用于机器学习的读者。我们的目的是教你如何训练你的第一个贝叶斯神经网络,并在TensorFlow上提供了入门示例。
为什么我们需要贝叶斯神经网络呢?传统的神经网络被训练用于产生一些相关变量的点估计。例如,我们可以使用历史数据来训练一个神经网络,预测未来某个时间点的股票价格。单一点估计的局限在于,它不能为我们提供任何关于此次预测中不确定性的度量。如果网络以95%的置信度预测股票将上涨,那么我们也许很容易就决定购买。但是,如果网络给出的置信度只有50%呢?在点估计情况下,我们将无法做出决定。相比之下,贝叶斯神经网络可以通过使用贝叶斯规则来估计预测中的不确定性。
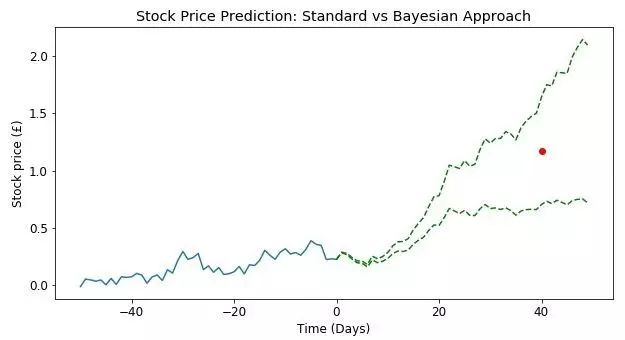
图中显示了在置信度为95%时未来40天内股票价格的点估计(红色圆圈)。由于没有评估不确定性,我们无法判断在交易时将承担多少风险。
关于教程
在本教程中,我们将了解:
· 贝叶斯统计如何应用于机器学习。
· 如何构建用于MNIST图像分类的贝叶斯模型。
· 贝叶斯神经网络如何量化预测中的不确定性。
想要了解更多关于贝叶斯神经网络的背景知识,Thomas Wiecki关于Bayesian Deep Learning的博客以及Yarin Gal的What my deep model doesn"t know... 博客都是非常好的入门参考。
本教程需要 TensorFlow1.1.0版本以及Edward1.3.1版本。
贝叶斯神经网络
要了解贝叶斯神经网络,我们将从贝叶斯统计的简要概述开始。 贝叶斯统计的核心是关于如何根据新的信息来改变人的信念。
贝叶斯法则
假设有两个事件a,b,想要计算在事件b发生的条件下事件a的条件概率,记作P(a|b)。贝叶斯法则定义如下:
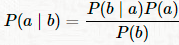
其中,P(b|a)是事件a发生的条件下事件b的条件概率。P(a)是事件a的先验概率,P(b)是事件b的先验概率。注意,对于变量a的先验概率是概率分布,并且我们得到的是在给定b的情况下,a的可能值的完整分布而不是单个点估计。
神经网络
那么,贝叶斯法则是如何应用到神经网络的呢?在本节我们将解释传统的神经网络是如何在某个特定假设下使用贝叶斯法则来训练。假定我们有一组数据集D={(x
i
,y
i
)}
N
i=1
,由数对输入x
i
和相应的输出y
i
组成,其中i=1,2,...,N。我们可以用神经网络来对似然函数P(y|x;ω)进行建模,其中ω是模型的一组可调参数,即网络的权重和偏差。例如对于分类问题,我们可以用标准的前馈网络,yi=f(x
i
;ω)后面是softmax层来归一化输出,以便它代表一个有效的质量函数P(y
i
|x
i
;ω)。
传统的神经网络训练方法通常通过优化权重和偏差来产生点估计,以最小化代价函数,例如分类问题情况下的交叉熵代价函数。从概率的观点来看,这相当于使观测数据P(D|ω)的对数似然最大化,以发现最大似然估计(MLE)Blundell et. al. 2015。
ω
MLE
=argmax
ω
logP(D|ω)=argmax
ω
∑
i=1
N
logP(y
i
∣x
i
,ω).
这种优化通常使用某种形式的梯度下降来执行(例如反向传播),之后当权重和偏差确定后,我们对于给定的输入x*预测一个新的输出y*=f(x*;ω)。
以这种方式训练神经网络容易过拟合,因此我们通常引入正则项例如L2。可以看出,对权重进行L2方法正则化等同于对权重进行正态高斯先验P(ω)~(0,I),并且最大化后验估计P(ω|D)。这就给了我们参数的最大后验估计(MAP)(详见MacKay著作的第41章):
ω
MAP
=argmax
ω
logP(ω|D)=argmax
ω
logP(D|ω)+logP(ω).
从这一点可以看出,传统的神经网络训练和正则化方法可以使用贝叶斯规则进行推理。贝叶斯神经网络进一步尝试近似整个后验分布P(ω|D)通过使用蒙特卡洛或变分推断技术。教程的余下部分将展示如何使用TensorFlow和Edward来实现这一过程。
数据导入
让我们用TensorFlow方法来导入MNIST images
In[1]:
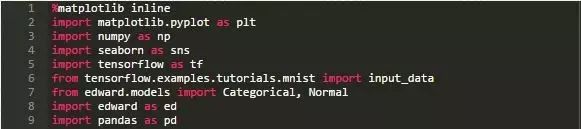
In[2]:

Extracting MNIST_data/train-images-idx3-ubyte.gz
Extracting MNIST_data/train-labels-idx1-ubyte.gz
Extracting MNIST_data/t10k-images-idx3-ubyte.gz
Extracting MNIST_data/t10k-labels-idx1-ubyte.gz
建模
回想一下,我们的任务是将手写的MNIST数字分类到{0,1,2,...,9}之一,并对分类的不确定性进行度量。我们的机器学习模型是一个简单的soft-max回归,为此我们首先需要选择似然函数来量化给定的一组参数(我们给定的权重和偏差)的观测数据的概率。我们将使用 Categorical似然函数(见第2章, Kevin Murphy的Machine Learning: a Probabilistic Perspective来了解Categorical分布(又称Multinoulli分布)的详细内容)。
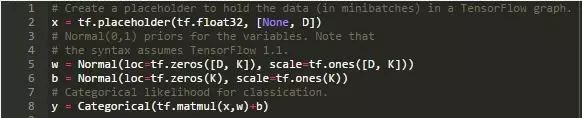
接下来我们在TensorFlow中设置一些占位符变量。这遵循与标准神经网络相同的过程,除了我们使用Edward库对权重和偏差引入先验。在下方代码中,我们引入了高斯先验。
In[3]:

In[4]:
变分推断
到现在为止我们已经定义了似然函数P(y|x,;ω)和先验P(ω),接下来我们将使用贝叶斯法则来计算后验P(ω|y,x)。然而我们面临着一个问题,即输出P(y)的概率对于大规模实例而言难于计算,因此我们并不试图直接计算后验。
为了解决这个问题,我们将用变分推断(VI)来代替。在变分推断中,我们选择一组关于参数ω的参数化分布Q(ω;λ)来近似真实的后验,然后优化参数λ,尽可能最佳地匹配真实的后验分布。这种方法的核心思想是将真正的后验P(ω|y,x)和近似分布Q(ω;λ)之间的Kullback-Leibler距离最小化,这可以被当作两个概率分布之间的不相似性的度量。
变分推断(VI)的原理远不是此博客中描述的内容所能涵盖的,更多相关信息可以通过Edward的文档或者Blei等人的论文《Variational Inference: A Review for Statisticians》了解。 MacKay的书也是一个不错的参考。
接下来我们将使用Edward库来设置权重和偏差的近似分布Q
ω
(ω)和Q
b
(ω):
In[5]:

In[6]:

In[7]:

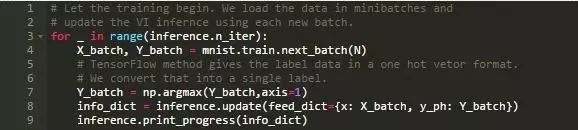
现在我们准备好执行变分推断了。我们加载了一个TensorFlow的session并开始迭代。这可能需要几分钟的时间...
In[8]:

In[9]:
5000/5000 100%

Elapsed: 5s | Loss: 27902.377
模型评估
现在我们已经准备好在测试数据上运行模型所需要的一切。贝叶斯模型评估的主要区别在于权重和偏差不存在单一值来评估模型。相应的,我们在模型中使用权重和偏差的分布,以便在最终预测中反映这些参数的不确定性。因此,我们不是单一的预测,而是得到一组预测及其准确率。
我们从后验分布中抽取100个样本,得到每个样本的执行结果。采样是一个较慢的过程,需要一段时间!
In[10]:






