二战期间,美军空军对作战飞机做了一次统计,统计发现,飞回来的飞机翅膀中弹特别多,机舱弹孔反而没多少。按照直觉推测,应该是加固机翼,可这逻辑对么?当然不对,事实上,恰恰应当加固机舱和发动机装甲。因为“飞回来的飞机”翅膀弹孔多,正说明打中翅膀了飞机还能回来,可打中机舱飞机就没救了,直接坠毁,根本不给你机会数弹孔。后来的实践证实了这一点,他们加固了机舱装甲,果然,飞机坠毁率下降了。人在江湖,处处是坑,懂得这个思维误区,就不容易掉坑里了。
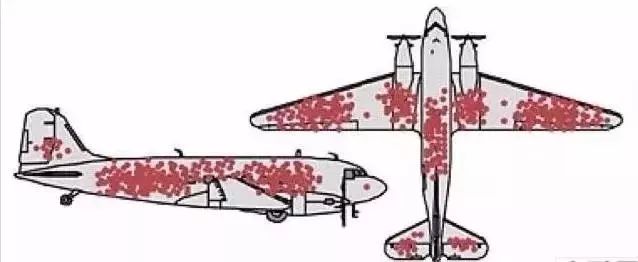
幸存者偏差:不要忽略那些沉默的大多数
何为“幸存者偏见”?
“幸存者偏见”,洋文写作“survivorship bias”或“survival bias”。这玩意儿属于“认知偏差”的一种。如果用一句通俗的话来概括“幸存者偏见”,就是【死人没法开口】。如果要说得更具体点,那就是:当你在分析某个事物的时候,可能会面对诸多的证据(样本)。但是大多数人通常只注意到【显式】的样本和证据,而忽略了【隐式】的样本和证据。从而得出错误的认知、错误的结论。
为了更形象一些,俺来说一下“幸存者偏见”的出处——古罗马的西赛罗(与凯撒同时代的知名政治家、文学家、演说家)讲过一个故事,大意如下:
有一群宗教信徒在某次沉船事故中幸存。幸存后捏,他们就找人作画(画面上是一群人在事故中祈祷),以此来宣扬说:因为他们作了虔诚的祷告,所以才在沉船事故中幸存。某信徒拿了这幅画给一个无神论者看。这个无神论者直接反问道:那些祈祷之后淹死的人,他们的画像在哪里?
以上就是“幸存者偏见”的出处。那些“祈祷之后依然淹死的人”,他们已经死了,不可能再去告诉别人,他们的祈祷失灵了。
不同领域中的“幸存者偏见”
西赛罗的那个故事,属于宗教领域的“幸存者偏见”。除了宗教领域,还有很多领域(甚至可以说,所有的领域)都会存在这类偏见。下面,俺挑选几个领域来举例。
IT 领域——创业的“银弹”
作为 IT 从业人员,俺经常在某些 IT 网站上看到某某公司的创业事迹。如果你也跟俺一样,估计这方面的故事也看了不少。不知你有没有发现,那些广为流传的创业案例,都是【成功】案例。越成功的,越具有传奇色彩,被宣传的次数就越多(比如乔布斯、盖茨)。相反,那些创业【失败】的案例,(相比而言)被提及的次数非常非常少。这会产生啥问题捏?
假设某个有志青年想要创业,他看了很多创业成功的案例,这些案例都提到某些共同的因素。于是捏,此人就误以为这些共同的因素是“银弹”——只要具备这些银弹,创业必定成功。这就如同西赛罗的那个故事——只看到存活的祈祷者,就误以为“祈祷”是存活的【充分条件】。
成功学领域——虚假的“充分条件”
说完“创业”,很自然就联想到“成功学”。那些鼓吹“成功学”的文章/书籍,通常存在很多谬误,其中一个谬误是——号称“某某方法论”是成功的【充分条件】。换句话说,只要具备了该方法论,就一定可以获得成功。
为啥俺说这是一个谬误捏?因为这些鼓吹成功学的文章/书籍,通常都【没有】去检验:该方法论是否也出现在失败者身上。只要有一个失败者也采用了该方法论,就足以说明——这个方法论【不是】成功的充分条件。比如说,很多成功学的理论提到了“勤奋”是成功的充分条件。但其实捏,勤奋而没有成功的,大有人在。
Python机器学习策略工作坊(第二期)开放报名
Python机器学习模块应用技能
Mongodb数据库处理大数据
机器学习策略代码模板与回测绩效
业界真实经验教学,打造全程真实编程体验
提供优质的机器学习量化策略源代码
通过五天高强度研习
最终实现动手编写实现机器学习策略代码。
2018年1月27日-31日 深圳
咨询电话/微信:18516600808

投资领域——仅凭运气的“股神”
最近半年,股市迎来新一轮的牛市行情。前几天有读者建议俺聊聊股市的话题,所以今天顺便拿投资领域来说事儿。
似乎在每一个国家的股市中,都有那么几个人被誉为“股神”。如果碰到牛市,被冠以“股神”的人还会再多出好几倍。(暂且【不】考虑“弄虚作假、谎报战绩”的情况)假设这些获得股神称号的人,都在实际操作过程中获得远高于大盘的收益率,他们有资格获得“股神”的称号吗?为了说明这个例子,俺转载某篇文章的其中一段(此文写于1984年)。
我要各位设想一场全国性的抛硬币大赛。让我们假定,全美国2.25亿人,在明天早晨起床时都掷一枚硬币,并猜硬币出现的正面或反面。如果猜对了,他们将从猜错者的手中赢得一美元。而猜错的人则被淘汰。
每天都有输家遭到淘汰,奖金则不断地累积。经过十个早晨的十次投掷之后,全美国约有22万人连续十次猜对抛硬币的结果。每人所赢得的资金约1000多美元。
现在,这群人可能会开始炫耀自己的战绩,此乃人的天性使然。即使他们仍保持谦虚的态度,但在鸡尾酒会中,他们偶尔会以此技巧吸引异性的注意,并炫耀他们对抛硬币的奇特洞察力。
游戏继续进行,再经过十天,约有215个人连续20次猜对抛硬币的结果,并且每个人赢得大约100万美元的奖金。输家总共付出2.25亿美元,赢家则得到2.25亿美元。
这时候,这群赢家会完全沉迷在自己的成就中——他们可能开始著书立说:“我如何每天早晨工作30秒,并在20天之内将—美元变成100万美元。”更糟的是,他们会在全国各地主办培训班,宣传如何有效地抛硬币。对那些持怀疑态度的学者,他们会反驳说:“如果你认为这是不可能的,该如何解释,为什么会有我们这215个人呢?”
但是,某些商学院的教授可能会粗鲁地指出—个事实——假如让2.25亿只猩猩参加这场比赛,结果大致上也是如此——会有215只猩猩连续赢得20次的投掷。
大伙儿知道这篇文章的作者是谁吗?作者就是被誉为“股神”的巴菲特。(1984年,为了纪念《证券分析》出版50周年,哥伦比亚大学搞了一次隆重的纪念活动,邀请到巴菲特作主题演讲。这篇文章就是当年的演讲稿)
大伙儿可能会觉得奇怪——难道巴菲特想要说明:“自己是运气好的猩猩”?当然不是啦。在那篇演讲的后续部分,巴菲特分析了——为啥他本人【不是】运气好的猩猩。在本文的结尾部分,俺还会再次提到这个演讲,以及巴菲特对“幸存者偏见”的分析。
虽然巴菲特不是“运气好的猩猩”,但俺敢肯定,某些所谓的“炒股高手”,只不过是“运气好的猩猩” :)
历史领域——莎草纸的误导
历史这个领域,简直可以说是“幸存者偏见”的重灾区。因为历史研究的是“过去发生的事情”。如果“过去的事情”距离现在比较遥远,很多相关的东西可能已经被时间消磨殆尽——沦为沉默的证据。下面,俺以“莎草纸”来说明“幸存者偏见”的误导性。
在地中海周边的古代文明(古埃及、腓尼基、古希腊、古罗马)都曾经使用莎草纸作为书写文字的载体。在保存至今的文物中,埃及的莎草纸文物比另外那三个地方要多。于是就很容易给人一种误解——似乎莎草纸在埃及用的比较广泛,而在另外三个地方使用不够广泛。但真实的原因是——莎草纸在潮湿环境中非常容易发霉腐烂,而埃及的气候比较干燥,于是保存下来的就比较多。
另一个例子是:曾经有一种学术观点认为腓尼基民族是“只擅长于经商而缺乏文艺细胞”。因为腓尼基留存至今的【少量】莎草纸都跟经商有关,并没有发现跟文学艺术相关的莎草纸文物。真的是这样吗?
俺个人认为,更大的可能性是:腓尼基人也有自己的文学艺术并且也保存在莎草纸上。但是那些腓尼基城市的气候非常不利于保存莎草纸,于是当地的莎草纸文物都腐烂了。至于少量涉及经商的莎草纸文件能保存至今,有可能是被经商船队带到其它地区(比如埃及这种干燥的地区),从而在其它地区保存了下来。
其它领域
在前面俺说了,几乎所有的领域,都可以看到“幸存者偏见”。限于篇幅,俺只列举前面这几个。对这个话题有兴趣的同学,可以在评论中补充。
“幸存者偏见”导致的问题
接下来,俺总结一下“幸存者偏见”可能导致的问题——分三个方面。
错误的认知 这个最好理解了——由于“错误的认知”会导致你对“沉默证据”的忽视,所以你对该领域的认知是不完全的。
错误的归因 在【只看到】“显式样本”的情况下,你可能会产生一些错误的归因。“幸存者偏见”导致的“错误归因”会有很多种。俺这里仅举几个例子。
因果倒置 想必大伙儿都看过举重比赛。对于举重运动员,很多人都有一个错误的观点——以为这些运动员是在练习举重之后,才导致身材变得矮壮。
但实际上捏,举重队在一开始筛选运动员的时候,就把那些身材细长的忽略掉了(这些身材细长的候选人,就是“沉默的样本”)。
换句话说,是因为他们身材矮壮,才有可能被选中去参加举重培训,而不是因为参加举重培训导致身材如此——这就是【因果倒置】。
牵强的归因(无中生有) 假设某个赌徒去赌场玩“押大小”(此游戏的胜负概率皆为 50%),连续赢了10次。对于大型赌场,每天来玩的人足够多,那么一段时间之后,总会出现某个赌徒玩“押大小”连续赢10次(甚至更多次)。从概率学的角度讲,这是很普通的。但是对该赌徒而言,如果他陷入了“幸存者偏见”这个误区,他就会企图给这个现象找到一个解释(进行“归因”)。假如此人是个宗教信徒,他/她可能会断言——有神明相助。
这就属于“牵强的归因”——把【随机事件】看作是有其它原因,并企图在随机性之外寻找一个解释。
错误的决策 还以刚才赌徒的例子来说事儿。
假设这个赌徒是宗教信徒,并且误以为自己连续赢10次是神明相助,那么他/她就会获得一种【虚假的信心】,并在这个“虚假信心”的支持下继续玩,甚至还会加大赌注/筹码。最后的结局很可能是——彻底输光。
这就是“幸存者偏见”导致的“错误决策”。如果你比较喜欢琢磨,可以把这个赌场的例子替换成天朝的牛市,你会发现其中有某些相通之处。
如何对付“幸存者偏见”?
在本文的最后部分,大致说一下:如何对付“幸存者偏见”?以下几个步骤,来自于俺粗糙的想法。
1、意识到“沉默证据”的存在
这是最起码的一点——你首先要能意识到“沉默证据”的存在。
这说起来容易,做起来很难——你需要形成这样一种思维习惯:每当看到“显式的证据”,你都要在内心反问:是否存在与之对应的“隐式证据”?
2、找到不同类型、不同层次的“沉默证据”
在前一条的基础上,你如果能找到“沉默的证据/隐式的证据”,自然就会获得更全面的认知。
有必要提醒一下:“隐式的证据”有时候不止一种类型。碰到这种情况,不是每个人都能想到所有的类型。
前面提到的“天朝舆论”的例子。那些思考问题不够深入的同学,通常只意识到“网管审查/删贴”导致的“沉默证据”,而忽略了更隐蔽的“沉默证据”——那些连上网条件都没有的人,是无法在网上表达不满的。
3、尝试排除“随机性”
决定一个样本会成为“隐式样本”or“显式样本”,有两种可能:
如果你在分析某个案例时,不清楚属于上述哪一种情况,那么你需要尝试去排除“随机性”。如果无法排除,那么你就只好认可该案例是“随机性”驱动的。具体该如何排除捏?在本文的最后,咱们重新回到本文开头提到的那篇巴菲特演讲。在说完“猩猩抛硬币”的游戏之后,巴菲特又说了如下一段话。通过这段话,你可以借鉴一下——如何规避“随机因素”的干扰。
然而,我必须说明,前述事例和我即将提出的案例,两者之间存在着若干重大差异。首先,
(a)如果你所选择的2.25亿只猩猩的分布状况大致上和美国的人口分布相同;
(b)如果经过20天的竞赛,只剩下215只赢家;
(c)如果你发现其中有40只猩猩来自于奥马哈的某个动物园,则其中必有蹊跷。
于是,你会询问该动物园的猩猩管理员,问此人各种问题。比如给这些猩猩吃什么饲料?这些猩猩是否做某些特殊的运动?是否看了什么书籍?……换言之,如果你发现成功案例有非比寻常的集中现象,则你希望判定此异常的特色是否是成功的原因。
科学的调查也遵循此一形态。如果你试图分析某种罕见癌症的原因——例如,美国每年只有1500个病例——而你发现蒙大拿州的某个矿区小镇便产生400个病例,则你必然对当地的饮水、病患的职业或其他种种变数产生兴趣。你知道,在一个小镇中发生400个病例,绝不是随机因素所造成。虽然你未必了解病因,但你知道从哪里着手调查。
除了地理,还有其他方式可以界定起源。除了地理的起源,还有我所谓“智力的起源”。我认为各位将会在投资领域中发现——不成比例的抛硬币赢家来自于一个极小的智力村庄.它可以称为“格雷厄姆一多德都市”。这个特殊智力村存在着许多赢家.这种集中现象绝非巧合所能够解释。
在某些情况下,即使非比寻常的集中现象也可能不重要。或许有100个只是模仿某一位极具说服力的领导者,而依其主张来猜测硬币的投掷结果。当他猜正面,这100个追随者也会自动地做相同的猜测。如果这一位领导者是属于最后215位赢家之一,则这100也便属于同一个智力起源,这项事实便不具有任何意义,因为100个案例实际上只代表一个案例。同理,假定你生活在一个父权结构极为严密的社会,而美国每一个家庭都恰好以父亲马首是瞻。20天之后,你将发现215位赢家是来自于21.5个家庭。若干天真的分析师可能因此而认为,成功地猜测硬币投掷的结果,其中具有高度的遗传因素。当然,这实际上不具有任何意义,因为你所拥有的不是215个独立的赢家,而只是21.5个随机分布的家庭。
我所要考虑的这一群成功投资者,拥有一位共同的智力族长——本杰明·格雷厄姆。但是,这些离开此智力家族的孩童,都是依据非常不同的方法猜测他们自己的“硬币”。他们各自前往不同的地方,买卖不同的股票和企业,但他们的综合绩效绝对无法用随机因素加以解释。他们做相同的猜测,并不是因为领导者下达某一项指令,因此也无法用这种方式解释他们的表现。族长只提供了猜测硬币的智力理论,每位学生都必须自行决定如何运用这项理论。
......
整个演讲很长,限于篇幅,就不全文转述了。
巴菲特那篇演讲的题目是《格雷厄姆-多德都市的超级投资者们》。“本杰明·格雷厄姆 和 大卫·多德”两人合著了《证券分析》一书(洋文叫“Security Analysis”)。此书被誉为“价值投资领域的圣经”;格雷厄姆本人被誉为“价值投资之父”。
上世纪50年代,巴菲特曾经在哥伦比亚大学选修了格雷厄姆开设的“证券分析课程”,并得了 A+ 的成绩。据传闻:格雷厄姆在哥伦比亚大学开设这门课程22年之后,才首次有学生(巴菲特)得到 A+ 的成绩。
结尾
本来这篇是纯讲心理学的。但是近期天朝的股市迎来“疯牛行情”,搞得很多网民人心浮动。所以俺顺便在本文中加入了跟投资领域有关的案例,再顺便推荐一下巴菲特的那篇演讲。
市面上讲巴菲特的书籍,简直是多如牛毛。但都是别人写的,质量也是鱼龙混杂。而本文推荐的这篇演讲,出自巴菲特本人的手笔,更有价值。
作者:编程-随想
编辑:爽临
来源:AnnieEasyFM(ID:shenqinvxia929)
打造属于你的“AlphaGo Zero”赚钱机器人!
介绍python分支循环语句
python下函数的创建与使用
K线数据, tick数据,非标准数据,json文件保存数据
统计套利分析, 寻找合适的配对
介绍vnpy的目标和定位……
时间:2018年1月13日-14日
地点:北京
报名电话/微信:18516600808
















