
以下文章内容,来自草堂君的新书《人人都会数据分析-从生活实例学统计》。因为新书中增添和细化了很多知识点,所以草堂君会逐步将这些内容补充到统计基础导航页中来,帮助大家建立数据分析思维。限于篇幅,只截取书中部分内容。
基础准备
前面介绍了四种抽样分布,它们分别针对不同的总体参数类型。有针对总体均值的Z分布和T分布,有针对总体方差的卡方分布,还有针对两个总体方差比的F分布。这些抽样分布将样本参数与总体参数联系在一起,从而能够通过样本特征推断总体的特征。大家可以点击下方文章链接回顾:
推断性统计分析包括三个分析手段:参数估计、参数假设检验和非参数假设检验,它们被称作数据分析的三板斧。前面两板“斧”主要应用于服从各种抽样分布的总体参数推断,可以利用样本的抽样分布对总体参数进行推断性分析,而非参数假设检验则主要针对总体分布情况不明的总体分布推断。
参数估计的类型
参数估计就是用抽样分布作为中介,用样本的参数特征对总体的参数进行数值估计的过程。根据总体参数估计结果的性质不同,可以分成两种参数估计类型:点估计和区间估计。参数估计主要围绕均值、方差和标准差展开。
点估计
点估计就是用某个具体的样本参数直接代表未知的总体参数,这是最简单的总体参数估计方式。例如,某市教育局在进行小学生身高水平调查,随机抽取1000名小学生作为样本,计算出样本平均身高为1.45米,如果直接用样本平均身高1.45米代表该市小学生的身高水平,那么这种估计方法就是点估计。
点估计虽然简便,但有明显的不足之处,那就是点估计不能显示出估计误差的大小。对于一个总体来说,总体参数是确定存在的常数值,但是从总体中抽取样本计算的样本参数却是随机变化的。例如,虽然该市第一次随机抽取的1000名小学生的平均身高是1.45米,但是第二次随机抽取1000名小学生的平均身高可能就是1.5米。用样本推断总体的过程必然存在估计误差,因此用点估计,即用某个具体的样本参数去代表总体参数是要冒很大风险的,这不是因为估计误差的存在,而是因为点估计的估计误差无法衡量,所以点估计主要用于为定性研究提供一定的数据参考,或者用在对总体参数估计精度要求不高的情况,在需要精确估计总体参数时,点估计是很少直接使用的。
区间估计
区间估计就是推断总体参数时,根据抽样分布的特征,给出可能包含总体参数的一个数值区间(点估计只是一个具体数值),同时给出总体参数落在这个区间的可能性,即概率保证。还是以小学生身高水平研究为例,如果用区间估计的方法估计该市小学生的平均身高水平,则有以下表达:根据随机抽取的1000名小学生样本,估计该市小学生的平均身高在1.4米到1.5米之间,置信水平为95%,这就是区间估计的结果表述,它不仅给出了平均身高的数值区间(置信区间),还有表示可信度的置信概率。
点估计虽然可以给出总体参数的估计值,但是点估计未能从样本跳跃到总体,仍然是对样本数据的描述,所以点估计属于描述性统计学的范畴。区间估计是从抽样分布出发,由样本参数到总体参数的推断,属于推断性统计学领域。
置信水平、置信区间和显著性水平
介绍区间估计时,涉及两个概念:置信区间和置信水平。置信区间是根据样本信息推导出来的可能包含总体参数的数值区间;置信水平表示置信区间的可信度。例如,对某市小学生平均身高的区间估计:有95%的置信度可以认为该市小学生的平均身高在1.4米到1.5米之间,(1.4米,1.5米)是置信区间,95%是置信水平,即有95%的信心认为这个区间包含该市小学生的平均身高。
置信水平表示为百分数,也可以称为置信度,表示成(1-α)100%的形式。α指的是显著性水平,表示总体参数不落在置信区间的可能性。置信水平和显著性水平是区间估计和假设检验的必备表述,用来表示样本推断总体的可信度。置信水平一般设为90%、95%和99%,相应的显著性水平为10%,5%和1%。
双侧置信区间和单侧置信区间
置信区间分为双侧置信区间和单侧置信区间。上面介绍的学生总体的平均身高的置信区间是(1.4米,1.5米),属于双侧置信区间,其中1.4米被称为置信下限,1.5米被称为置信上限。在某些场合,我们只关心总体参数置信区间某一侧的界限。例如,对于商品的使用寿命来说,消费者只关心其寿命的下限,也就是该商品最短能使用多长时间,对其置信上限则希望越长越好。与使用寿命相反,生产者更关心生产成本最高会达到多少。
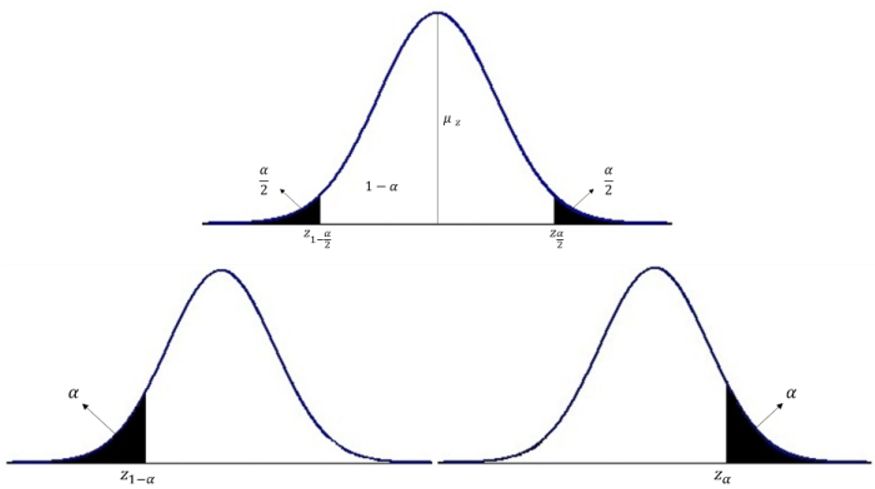
以均值抽样分布的分布为例,如下图所示,上方的图表示双侧置信区间,显著性水平被平分到分布曲线的两端;下方两张图则表示单侧置信区间,显著性水平全部位于曲线的一端,如果只关心置信下限,则落于左端,反之,则落于右端。
温馨提示:



















