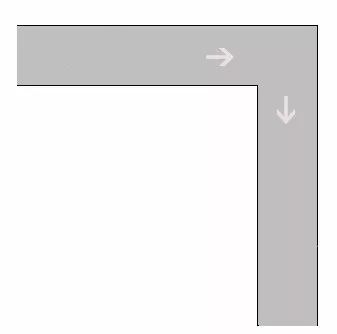
海森堡和小粉用家具厂作为伪装
将 dope 作坊隐匿其中
如今他们的任务就是在沙发中塞满 dope
然后从家具厂后门的小巷子偷偷运出去
但是……
扩展猫粮
视频中,老白和小粉两个人想尽办法把沙发面积做大,这样就可以提高单次的搬运量,减少搬运次数,从而降低风险。虽然这种求知的精神值得我们学习,但希望大家无论如何都不要沾染毒品,因为无论怎样挖空心思旁门左道,都不会有好下场的。嗯。
话说绝命毒师的衍生剧《Better Call Saul》已经在今年夏天更完第三季了,还没看的小伙伴可以去看看。


言归正传。本期问题的名字其实非常耿直,就叫“Moving Sofa Problem”,由数学家
Leo Moser
在1966年提出:在一个宽度为1的直角右拐弯道中,能够通过弯道的最大图形长什么样?最大面积是多少?
小粉提出的两个方案
按照小粉高中没毕业的数学水平,很容易想到视频中的前两个方案:
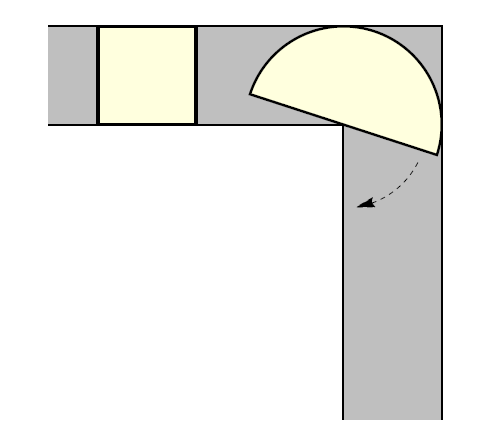
其中正方形面积是
1
,半圆形
面积
是
1.571
(π/2)。由于计算实在过于简单,小粉遭到了老白的嫌弃与不屑。身为一个受过高等教育的知识分子、一个把脑袋别在裤腰带上的毒贩,老白追求的是
效率
!!毕竟每多运一次沙发,就多一分的风险,所以沙发面积要尽可能的大。有的同学可能会问,费这劲干嘛?花点儿钱把通道加宽一些不好吗?
不好。
“老白改良前”和“老白改良后”
老白的第一个方案,也就是改良前的方案,最早由数学家
John Hammersley
提出:
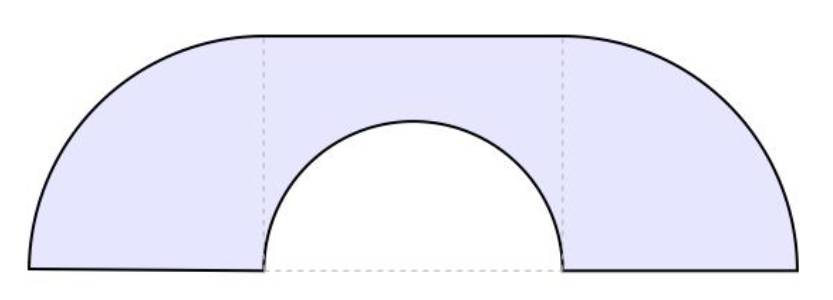
如图,
左右两边
各有一个面积一样大的1/4圆,这两个1/4圆刚好是由小粉提到的那个半圆平分而成的。
中间的部分
也不难,它原本是一个长度为4/π的矩形,后来中间被挖掉了一个半径为2/π的半圆。左、中、右三个部分结合在一起,就组成了一个面积高达
2.2074
的沙发。
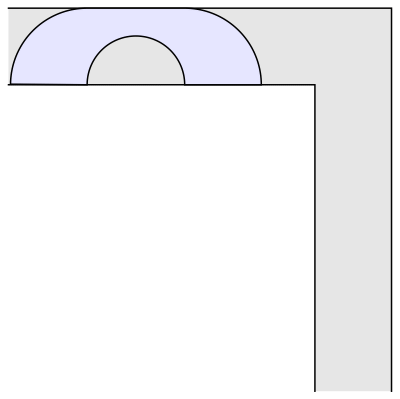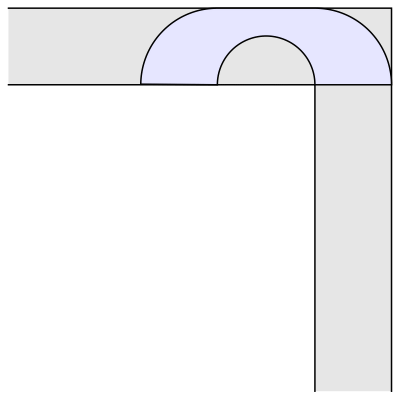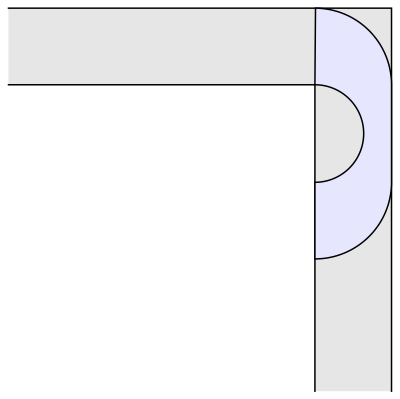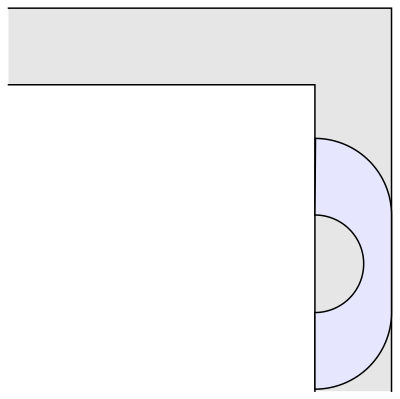
乍一看上去,这个方案还真的有点儿客厅长沙发的样子。可惜若大的沙发上只有你一个人孤零零地躺着,没有友仔玩,也没有友女玩,只好看看动漫打打游戏维持生活这样子……
……
后来在1992年,数学家
Joseph Gerver
给出了面积更大的改良版方案,也就是视频中的“老白改良后沙发”:
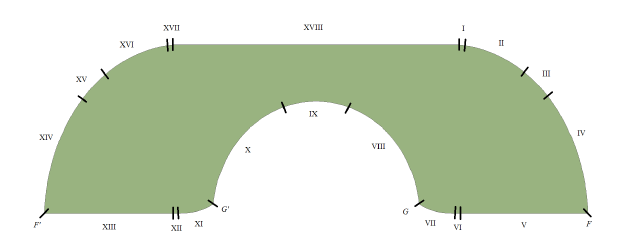
这个方案一共有18部分,其中有3条直线,其余都是曲线。看起来很复杂?其实它并不难。只需先这样,再这样,然后这样……最后再施展一些绚丽的数学技巧……我们就能算出它的面积:
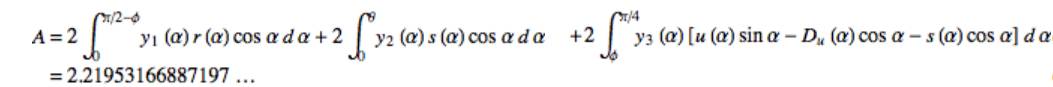
(完整过程: http://mathworld.wolfram.com/MovingSofaProblem.html)
保留4位小数的话就是
2.2195
,比之前的2.2074大了约莫……1%……
这1%,便是一名退休化学教师的骄傲与尊严。
那么,这个沙发还能再改良吗?面积还能更大吗?它会不会就是最优解呢?
改良版沙发的一个证明思路
这个问题至今为止还没有定论。不过,一位叫做
Philip E Gibbs
的数学家在计算机的帮助下,给出了一种“另类”的证明方案,大概思路就是——首先固定一个沙发,然后用一个直角的弯道模型往沙发上“套”,这个过程有点儿像我们用模具做饼干一样:

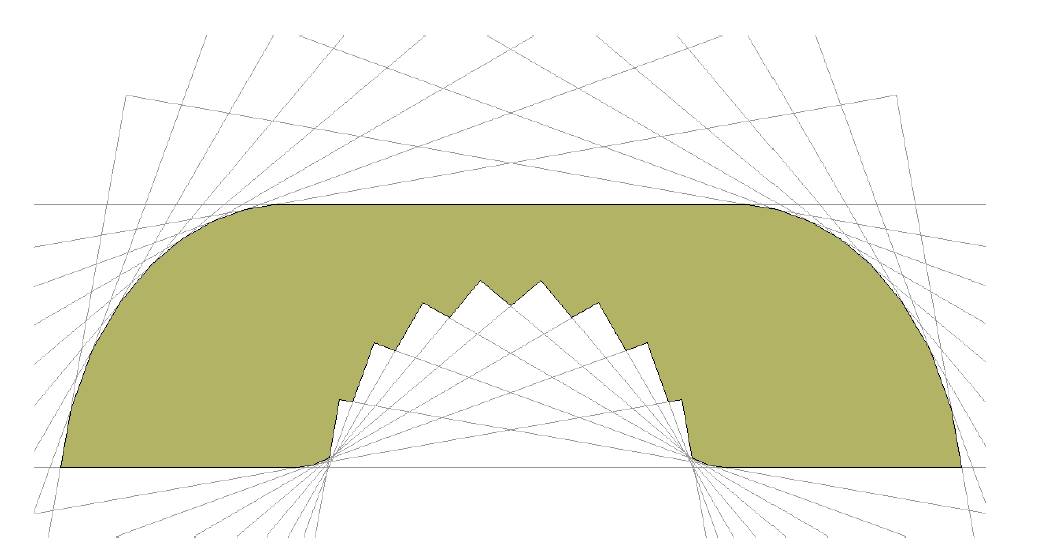
被直角弯道模具套了3次的沙发长这样(上下两条水平线是一次,两个直角是另外两次):
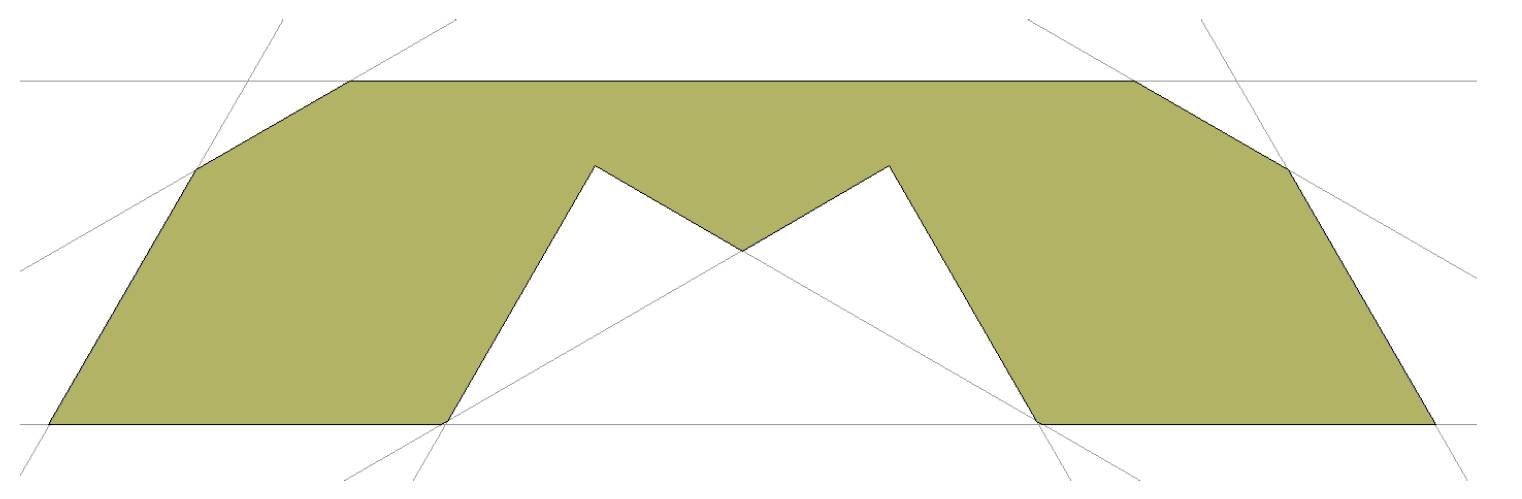
9次之后: