台大机器学习课程学习笔记5
Training versus Testing
上节课,我们主要介绍了
机器学习的可行性
。首先,由NFL定理可知,机器学习貌似是不可行的。但是,随后引入了统计学知识,如果样本数据足够大,且hypothesis个数有限,那么机器学习一般就是可行的。
本节课将讨论机器学习的核心问题,严格证明为什么机器可以学习。
从上节课最后的问题出发,即当hypothesis的个数是无限多的时候,机器学习的可行性是否仍然成立?
我们先来看一下基于统计学的机器学习流程图:
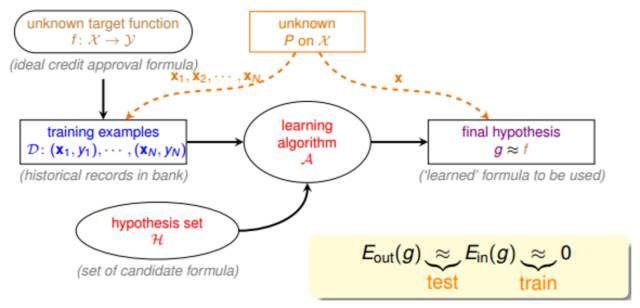
该流程图中,训练样本D和最终
测试
h的样本都是来自
同一个数据分布
,这是机器能够学习的前提。
另外,训练样本D应该足够大,且hypothesis set的个数是有限的,这样根据霍夫丁不等式,才不会出现Bad Data,保证
E
in
≈ E
out
,即有很好的泛化能力。
同时,通过训练,得到使
E
in
最小的h,作为模型最终的矩g,g接近于目标函数。
这里,我们总结一下前四节课的主要内容:
第一节课,我们介绍了机器学习的定义,目标是找出最好的矩g,使g≈f,保证
E
out
(g)
≈0;
第二节课,我们介绍了如何让
E
in
≈0,可以使用PLA、pocket等演算法来实现;
第三节课,我们介绍了机器学习的分类,我们的训练样本是批量数据(batch),处理监督式(supervised)二元分类(binary classification)问题;
第四节课,我们介绍了机器学习的可行性,通过统计学知识,把
E
in
(g)
与
E
out
(g)
联系起来,证明了在一些条件假设下,
E
in
(g) ≈ E
out
(g)
成立。

这四节课总结下来,我们把机器学习的
主要目标
分成两个核心的问题:
-
E
in
(g) ≈ E
out
(g)
-
E
in
(g)
足够小
上节课介绍的机器学习可行的一个条件是hypothesis set的个数M是有限的,那M跟上面这两个核心问题有什么联系呢?
我们先来看一下,当M很小的时候,由上节课介绍的霍夫丁不等式,得到
E



