专栏名称: 算法与数学之美

从生活中挖掘数学之美，在实践中体验算法之奇，魅力旅程，从此开始！

极限导论

算法与数学之美 · 公众号 · 算法 · 2017-01-10 22:37

正文

来源：图灵社区

编辑:Gemini

如果没有极限的概念, 那么微积分将不复存在. 这意味着, 我们将用大量的时间来研究它们. 事实证明, 虽然恰当地定义一个极限是件相当棘手的事情, 但你仍然有可能对极限有个直观理解, 而无须深入其中的具体细节. 这对于解决微分和积分问题已经足够了. 因此, 本章仅仅包含对极限的直观描述; 正式描述请参见附录 A. 总的来说, 以下就是我们会在本章讲解的内容：

对于极限是什么的直观概念;
左、右与双侧极限, 及在 ∞ 和 -∞ 处的极限;
何时极限不存在;
三明治定理 (也称作 “夹逼定理”).

1.1　极限：基本思想

让我们开始吧. 我们从某个函数 f 和 x 轴上的一点出发, 该点称为 a. 需要理解的是：当 x 非常非常接近于 a, 但不等于 a 时, f (x) 是什么样子的？这是一个非常奇怪的问题, 人类相对晚近才发展出微积分很可能就是因为这个原因吧.

这里有一个例子, 说明了为什么要提出这样的问题. 令 f 的定义域为
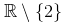
(除 2 以外的所有实数), 并设 f (x) = x - 1. 这可以写作：

f (x) = x - 1　当 x ≠ 2.

这看起来好像是一个古怪的函数. 毕竟, 到底为什么要将 2 从定义域中去除掉呢？其实, 在下一章就会看到, f 很自然地就是个有理函数 (参见 4.1 节的第二个例子) 不过现在, 让我们姑且接受 f 的定义, 并画出其图像, 如图 3-1 所示.

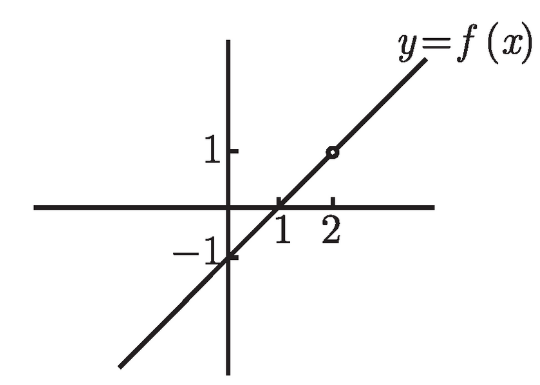
图　3-1

那么 f (2) 是什么呢？或许你会说 f (2) = 1, 但这是大错特错了, 因为 2 根本不在 f 的定义域中. 你所能给出的最好回答就是 f (2) 是无定义的. 另一方面, 当 x 非常非常接近于 2 的时候, 我们可以找到一些 f (x) 的值, 并看看将会有什么发生. 例如, f (2.01) = 1.01, f (1.999) = 0.999. 稍作思考, 你会发现当 x 非常非常接近于 2 的时候, f (x) 的值会非常非常接近于 1.

还有, 只要令 x 充分地接近于 2, 那么你想多接近于 1 就能多接近于 1, 却又不是真的达到 1. 例如, 如果你想要 f (x) 在 1 ± 0.0001 内, 可以取在 1.9999 和 2.0001 之间的任意的 x 值 (当然, 除了 x = 2, 这是禁止的). 如果你想要 f (x) 在 1 ± 0.000 007 内, 那么选取 x 的时候, 你不得不更细心一点. 这一次, 你需要取在 1.999 993 和 2.000 007 之间的任意值了 (当然, 还是除了 2).

这些思想会在附录 A 的 A.1 节里有更详细的描述. 不过现在, 让我们回到正题, 直接写出

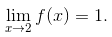
如果你大声将它读出来, 它听起来应该像是 “当 x 趋于 2, f (x) 的极限等于 1”. 再次说明, 这意味着, 当 x 接近于 2(但不等于 2) 时, f (x) 的值接近于 1. 那到底有多近呢？你想要多近就能多近. 以上陈述的另外一个写法是

f (x) → 1 当 x → 2.

这个写法更难用来计算, 但其意义很清晰：当 x 沿着数轴从左侧或者从右侧趋近于 2 时, f (x) 的值会非常非常接近于 1(并保持接近的状态!).

现在, 取上述函数 f 并对它做一点改动. 假设有一个新的函数 g, 其图像如图 3-2 所示.

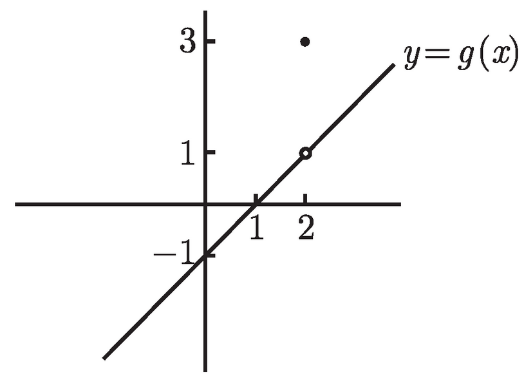
图　3-2

函数 g 的定义域是所有实数, 并且 g (x) 可以被定义为如下的分段函数：

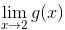是什么呢？这里的关键是, g(2) 的值和该极限是不相关的! 只有那些在 x 接近于 2 时的 g(x) 的值, 而不是在 2 处的值, 才是问题的关键. 如果忽略 x = 2, 函数 g 和之前的函数 f 就是完全相同的. 因此, 尽管 g(2) = 3, 我们还是有

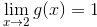
这里的要点是, 当你写出

的时候, 等式左边实际上不是 x 的函数! 要记住, 以上等式是说, 当 x 接近于 2 时, f (x) 接近于 1. 事实上, 我们可以将 x 替换成其他任意字母, 上式仍然成立. 例如, 当 q 接近于 2 时, f (q) 接近于 1, 因此我们有

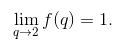
也可以写成

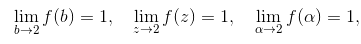
如此等等, 直到用光了所有的字母和符号! 这里的要点是, 在极限

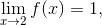
中, 变量 x 只是一个虚拟变量. 它是一个暂时的标记, 用来表示某个 (在上述情况下) 非常接近于 2 的量. 它可以被替换成其他任意字母, 只要替换是彻底的; 同样, 当你求出极限的值时, 结果不可能包含这个虚拟变量. 所以对虚拟变量你要灵活处理.

1.2　左极限与右极限

我们已经看到, 极限描述了函数在一个定点附近的行为. 现在想想看, 你会如何描述图 3-3 中 h (x) 在 x = 3 附近的行为.

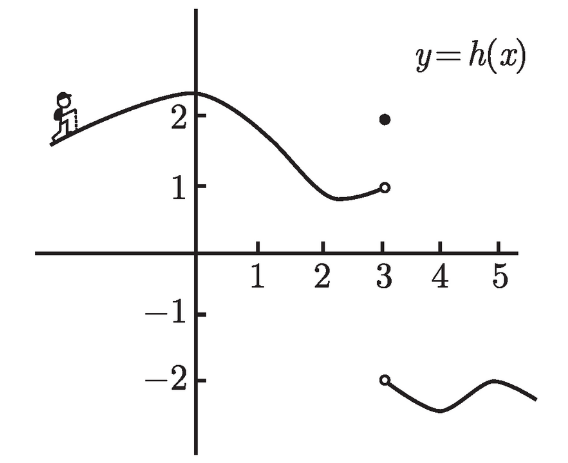
图　3-3

当然, 就趋于极限的行为而言, h (3) = 2 实际上是无关紧要的. 现在, 当你从左侧接近于 x = 3 时会发生什么呢？想象一下, 你是图中的远足者, 顺着山势上下. h (x) 的值会告诉你, 当你的水平位置是 x 时, 你所在高度是多少. 因此, 如果你从图的左边向右走, 那么当你的水平位置接近于 3 时, 你所在高度就会接近于 1. 当然, 当到达 x = 3 时你会陡然坠落 (更不用说那个古怪的小突起), 但暂时我们不关心. 这时任何在 x = 3 右侧的值, 包含 x = 3 本身对应的值, 都是无关紧要的. 因此, 就可以看到 h (x) 在 x = 3 的左极限等于 1.

另一方面, 如果你从图的右边向左走, 那么当你的水平位置接近于 x = 3 时, 你所在高度就会接近于 -2. 这就是说, h (x) 在 x = 3 的右极限等于 -2. 这时任何在 x = 3 左侧 (包含 x = 3 本身) 的值都是无关紧要的.

可将上述发现总结如下：

　及　.

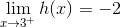在上面第一个极限中 3 后的小减号表示该极限是一个左极限, 第二个极限中 3 后的小加号表示该极限是一个右极限. 要在 3 的后面写上减号或加号, 而不是在前面, 这是非常重要的! 例如, 如果你写成

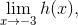
那么指的是 h (x) 在 x = -3 时的通常的双侧极限, 而不是 h (x) 在 x = 3 时的左极限. 这确实是两个完全不同的概念. 顺便说一下, 在左极限的极限符号底下写 x → 3+ 的理由是, 此极限只涉及小于 3 的 x 的值. 也就是说, 你需要在 3 上减一点点来看会有什么情况发生. 类似地, 对于右极限, 当你写 x → 3+ 的时候, 这意味着你只需要考虑如果在 3 上加一点点会有什么情况发生.

正如我们将在下一节看到的, 极限不是总存在的. 但这里的要点是：通常的双侧极限在 x = a 处存在, 仅当左极限和右极限在 x = a 处都存在且相等! 在这种情况下, 这三个极限 (双侧极限、左极限和右极限) 都是一样的. 用数学的语言描述, 我们说,

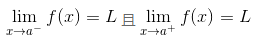等价于

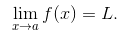
如果左极限和右极限不相等, 例如上述例子中的函数 h, 那么双侧极限不存在. 我们写作

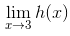
不存在或使用缩写 “DNE” 表示 “不存在”.

1.3　何时不存在极限

我们刚刚看到, 当相应的左极限和右极限不相等时双侧极限不存在. 这里有一个更戏剧性的例子. 考虑 f (x) = 1/x 的图像, 如图 3-4 所示. 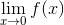是什么呢？双侧极限在那里不大可能存在. 因此, 我们先来试着求一下右极限, 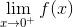. 看一下图像, 当 x 是正的且接近于 0 时, f (x) 看起来好像非常大. 特别是, 当 x 从右侧滑到 0 时, 它看起来并不接近于任何数; 它就是变得越来越大了. 但会有多大呢？它会比你能想象到的任何数都大! 我们说该极限是无穷大, 并写作

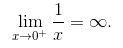
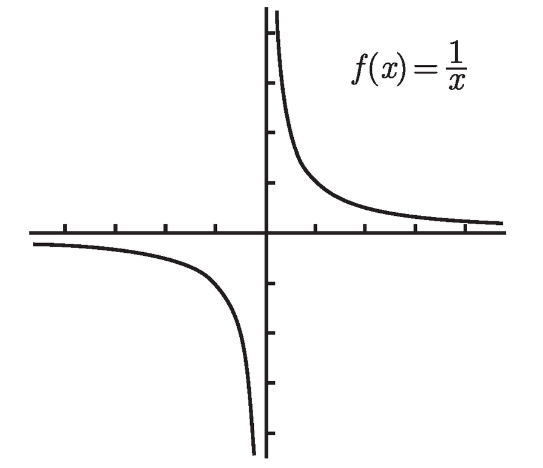
图　3-4

类似地, 这里的左极限是 -∞, 因为当 x 向 0 上升时, f (x) 会变得越来越负. 这就是说

由于左极限和右极限不相等, 故双侧极限显然不存在. 另一方面, 考虑函数 g, 其定义为 g (x) = 1/x2, 其图像如图 3-5 所示.

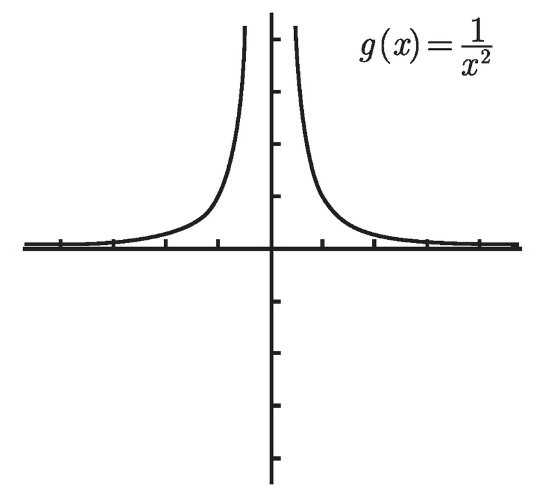
图　3-5

此函数在 x = 0 处的左极限和右极限都是 ∞, 因此你也可以说 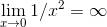. 顺便说一下, 现在我们有了一个关于 “垂直渐近线” 的正式定义：

现在, 可能会出现左极限或右极限不存在的情况吗？答案是肯定的! 例如, 让我们来看一个怪异的函数 g, 其定义为 g (x) = sin (1/x). 此函数的图像看起来会是什么样的呢？首先, 让我们来看一下 x 的正值. 由于 sin (x) 在 x = π, 2π, 3π, ··· 上的值全为 0, 因而 sin (1/x) 在 1/x = π, 2π, 3π, ··· 上的值全为 0. 我们取其倒数, 会发现 sin (1/x) 在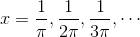上的值全为 0. 这些数就是 sin (1/x) 的 x 轴截距. 在数轴上, 它们看起来如图 3-6 所示.

图　3-6

正如你看到的, 当接近于 0 的时候, 它们都挤在了一起. 由于在每一个 x 轴截距之间, sin (x) 向上走到 1 或向下走到 -1, 因此, sin (1/x) 也一样. 把目前已知的画出来, 可得到图 3-7.

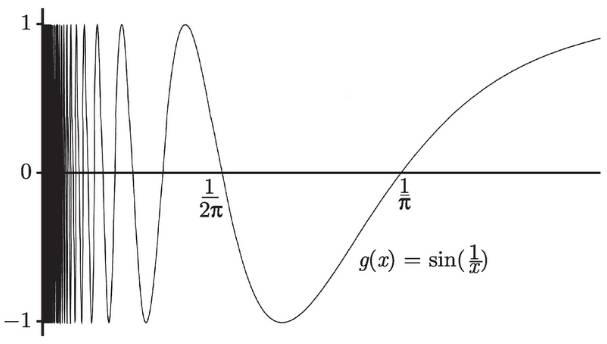
图　3-7

那么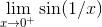是什么呢？以上图像在 x = 0 附近很杂乱. 它无限地在 1 和 -1 之间振荡, 当你从右侧向 x = 0 处移动时, 振荡会越来越快. 这里没有垂直渐近线, 也没有极限1. 当 x 从右侧趋于 x = 0 时, 该函数不趋于任何数. 因此可以说, 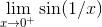不存在 (DNE). 我们会在下一节将 y = sin (1/x) 的图像补充完整.

1正式的证明请参见附录 A 的 A.3.4 节.

1.4　在 ∞ 和 -∞ 处的极限

还有一类需要研究的极限. 我们已经研究了在接近一点 x = a 时的函数行为. 然而在有些情况下, 重要的是要理解当 x 变得非常大时, 一个函数的行为如何. 换句话说, 我们感兴趣的是, 研究当变量 x 趋于 ∞ 时函数的行为. 我们想写出

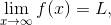
并以此表示, 当 x 很大的时候, f (x) 变得非常接近于值 L, 并保持这种接近的状态. (更多详情请参见附录 A 的 A.3.3 节. ) 重要的是要意识到, 写出 “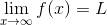” 表示 f 的图像在 y = L 处有一条右侧水平渐近线. 类似地, 当 x 趋于 -∞ 时, 我们写出

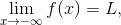
它表示当 x 变得越来越负 (或者更确切地说, -x 变得越来越大) 时, f (x) 会变得非常接近于值 L, 并保持接近的状态. 当然, 这对应于函数 y = f (x) 的图像有一条左侧水平渐近线. 如果愿意, 你也可以把这些转化为定义：

当然, 像 y = x2 这样的函数没有任何水平渐近线, 因为当 x 变得越来越大时, y 值只会无限上升. 用符号表示, 我们可以写作 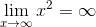. 反过来, 极限也有可能不存在. 例如, 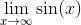. sin (x) 会变得越来越接近何值 (并保持这种接近状态)呢？它只是在 -1 和 1 之间来回振荡, 因此绝不会真正地接近任何地方. 此函数没有水平渐近线, 也不会趋于 ∞ 或 -∞; 你所能作的最好回答是, 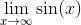不存在 (DNE). 证明请参见附录 A 的 A.3.4 节.

让我们回到上一节看到的函数 f , 其定义为 f (x) = sin (1/x). 当 x 变得非常大时会怎么样呢？首先, 当 x 很大时, 1/x 会非常接近于 0. 由于 sin (0) = 0, 那么 sin (1/x) 就会非常接近于 0. x 越大, sin (1/x) 就会越来越接近于 0. 我的论证有点粗略, 但希望能说服你相信2

2如果你不信, 请参见附录 A 的 A.4.1 节!

因此, sin (1/x) 在 y = 0 处有一条水平渐近线. 这就能够扩展我们之前画的 y = sin (1/x) 的图像, 至少是向右边做扩展. 我们仍旧担心当 x

注意到我们使用了 sin (x) 是 x 的奇函数的事实来由 sin (-1/x) 得到 -sin (1/x). 这样一来, 由于奇函数有一个很好的性质, 就是其图像关于原点对称 (参见 1.4 节), 可以完整地画出 y = sin (1/x) 的图像, 如图 3-8 所示.

图　3-8

同样, 很难画出当 x 在 0 附近时的情况. x 越接近 0, 此函数就会振荡得越激烈. 当然, 该函数在 x = 0 处无意义. 在上图中, 我选择避免在中间画得密密麻麻, 而是把那里的激烈振荡留给你想象.

大的数和小的数

希望我们都认同 1 000 000 000 000 是一个大的数. 那么 -1 000 000 000 000 呢？或许这会引起争议, 但我要让你把它看作是一个大的负数, 而不是一个小的数. 举个小的数的例子, 0.000 000 001, 同时 -0.000 000 001 也是一个小的数 (更确切地说, 是一个小的负数). 有趣的是, 我们不打算把 0 看作是个小的数：它就是零. 因此, 下面就是我们对于大的数和小的数的非正式定义：

如果一个数的绝对值是非常大的数, 则这个数是大的;
如果一个数非常接近于 0(但不是真的等于 0), 则这个数是小的.

尽管上述定义在我们的实际应用中很有帮助, 但这实在是一个没有说服力的定义. “非常大” 和 “非常接近于 0” 分别意味着什么？好吧, 我们考虑极限

正如之前看到的, 它表示当 x 是一个足够大的数时, f (x) 的值就会几乎等于 L. 可问题是, 多大才是 “足够大” 呢？这取决于你想让 f (x) 距离 L 有多近! 不过, 从实际应用的角度出发, 如果 y = f (x) 的图像看上去开始变得靠近在 y = L 的水平渐近线, 那么这个数 x 足够大. 当然, 一切都依赖于函数 f 的定义, 例如图 3-9 中的两种情况.

图　3-9

在这两种情况下, f (10) 都不在 L 的附近. 在左图中, 当 x 至少是 100 时, f (x) 看上去非常接近于 L, 因此, 任何比 100 大的数都是大数. 在右图中, f (100) 远离 L, 因此, 现在的 100 就不是足够大了. 在这种情形下, 你可能需要走到 200. 那么你能够只选取一个像 1 000 000 000 000 这样的数, 然后说它已经很大了吗？不可以, 因为一个函数有可能一直起伏不定, 直到比如 5 000 000 000 000 才变得趋于它的水平渐近线. 这里的要点是, “大的” 一词必须考虑到相关的某个函数或极限才有意义. 幸好, 没有最大, 只有更大, 往上还大有余地 —— 甚至一个像 1 000 000 000 000 这样的数, 相对于 10100 (古戈尔) 来说还是相当小, 而 10100 与 101 000 000 比起来又是那么微不足道 …… 顺便说一下, 我们会经常使用术语 “在 ∞ 附近” 来代替 “大的正的数”. (在字面意义上说, 一个数不可能真的在 ∞ 附近, 因为 ∞ 无穷远. 不过在 x → ∞ 时的极限的语境中, “在 ∞ 附近” 的说法还是说得通的.)

当然, 所有这些也都适用于 x → -∞ 时的极限, 你只需在上述所有大的正的数之前添加一个负号. 在这种情况下, 我们有时会说 “在 -∞ 附近” 来强调我们所指的是大的负的数.

另一方面, 我们会经常看到极限

或　.

在上述三种情况下, 我们知道, 当 x 足够接近于 0 时, f (x) 的值几乎是 L. (对于右极限, x 还必须为正; 而对于左极限, x 还必须为负. ) 那么 x 必须离 0 多近呢？这取决于函数 f . 因此, 当说一个数是 “小的”(或者 “接近于 0”) 时, 必须结合某个函数或极限的语境来考虑, 就像在 “大的” 情形中一样.

尽管这一番讨论让之前的非正式定义确实变得更严谨了一些, 但它仍不算完美. 如果你想了解更多, 真的应该查看一下附录 A 的 A.1 节和 A.3.3 节.

1.5　关于渐近线的两个常见误解

现在是时候来纠正一些关于水平渐近线的常见误解了. 首先, 一个函数不一定要在左右两边有相同的水平渐近线. 在 3.3 节 f (x) = 1/x 的图像中, 左右两侧都有 y = 0 这条水平渐近线. 也就是说,

　和　.

然而, 考虑图 3-10 中 y = tan-1 (x) (或反三角函数 y = arctan (x), 你可以使用这两种写法中的任意一种) 的图像.

图　3-10

此函数在 y = π/2 处有一条右侧水平渐近线, 在 y = -π/2 处有一条左侧水平渐近线, 它们是不同的. 也可以用极限来表示：

因此, 一个函数的确可以有不同的右侧和左侧水平渐近线, 但最多只能有两条水平渐近线 (一条在右侧, 另一条在左侧). 它也有可能一条都没有, 或者只有一条. 例如, y = 2x 有一条左侧水平渐近线, 但没有右侧水平渐近线 (参见 1.6 节的图像). 这和垂直渐近线相反：一个函数可以有很多条垂直渐近线 (例如, y = tan (x) 有无穷多条垂直渐近线).

另外一个常见误解是, 一个函数不可能和它的渐近线相交. 或许你曾学到, 渐近线是一条函数越来越接近但永远不会相交的直线. 这并不正确, 至少当你讨论的是水平渐近线时. 例如, 考虑定义为 f (x) = sin (x) /x 的函数 f , 这里我们只关心当 x 是很大的正数时的函数行为. sin (x) 的值在 -1 和 1 之间振荡, 因此, sin (x) /x 的值在曲线 y = -1/x 和 y = 1/x 之间振荡. 此外, sin (x) /x 和 sin (x) 有相同的零点, 即 π, 2π, 3π, ··· . 综合所有的信息, 其图像如图 3-11 所示.

图　3-11

图像中用虚线表示的曲线 y = 1/x 和 y = -1/x 形成了正弦波的包络. 毫无疑问, 正如你从图像中看到的,

必定成立. 这意味着, x 轴是 f 的水平渐近线, 尽管 y = f (x) 的图像与 x 轴一次又一次地相交. 为了证明上述极限, 我们需要应用所谓的三明治定理. 这个证明就在下一节的结尾部分.

1.6　三明治定理

三明治定理 (又称作夹逼定理) 说的是, 如果一个函数 f 被夹在函数 g 和 h 之间, 当 x → a 时, 这两个函数 g 和 h 都收敛于同一个极限 L, 那么当 x → a 时, f 也收敛于极限 L.

以下是对该定理的一个更精确的描述. 假设对于所有的在 a 附近的 x, 我们都有 g (x) ≤ f (x) ≤ h (x), 即 f (x) 被夹在 g (x) 和 h (x) 之间. 此外, 我们假设且 . 那么我们可以得出结论：; 即当 x → a 时, 所有三个函数都有相同的极限. 一如往常, 一图胜千言 (见图 3-12).

图　3-12

在图像中用实线表示的函数 f 被夹在其他两个函数 g 和 h 之间; 当 x → a 时, f (x) 的极限被迫趋于 L. (三明治定理的证明参见附录 A 的 A.2.4 节. )

对于单侧极限, 我们也有一个类似版本的三明治定理, 只是这时不等式 g (x) ≤ f (x) ≤ h (x) 仅在 a 的我们关心的一侧成立. 例如,

是什么呢？y = x sin (1/x) 的图像和 y = sin (1/x) 的图像很相似, 只是现在, 前面有一个 x 致使函数陷于包络 y = x 和 y = -x 之间. 图 3-13 是 x 在 0 和 0.3 之间时的函数图像.

图　3-13

从图中可以看到, 当 x 趋于 0 时, 函数仍旧有激烈的振荡, 但现在它们被包络线抑制着. 特别是, 这里求我们想要的极限正是三明治定理的一个完美应用. 函数 g 是下方的包络线 y = -x, 而函数 h 是上方的包络线 y = x. 我们需要证明对于 x > 0, 有 g (x) ≤ f (x) ≤ h (x). 由于只需要 f (x) 在 x = 0 处的右极限, 所以我们不关心 x 0 时, 要怎样证明 g (x) ≤ f (x) ≤ h(x) 呢? 我们将会用到任意数 (在我们的例子中是 1/x) 的正弦都处于 -1 和 1 之间这一事实：

现在用 x 乘以这个不等式, 由于 x > 0, 得到

而这正是我们需要的 g (x) ≤ f (x) ≤ h (x). 最后, 注意到

及　.

因此, 由于当 x → 0+ 时, 夹逼的函数 g (x) 和 h (x) 的值收敛于同一个数 0, 所有 f (x) 也一样. 也就是说, 证明了

要记住, 如果前面没有因子x, 上式显然不成立; 正如我们在3.3 节看到的, 当 x → 0+ 时, sin (1/x) 的极限不存在.

我们还没有解决上一节结尾部分的那个极限证明问题! 回想一下, 要证明的是

为了证明此式, 需要用到三明治定理一个稍有不同的形式, 涉及在 ∞ 处的极限. 在这种情况下, 如果对于所有的很大的 x, 都有 g (x) ≤ f (x) ≤ h (x) 成立; 又如果已知且 . 就可以说, . 这与有限处极限的三明治定理几乎是一样的. 为了确立上述极限, 还要用到, 对于所有的 x, 都有 -1 ≤ sin (x) ≤ 1, 但这次, 对于所有的 x > 0, 要用该不等式除以 x 得到