1 感知机
感知机是
二分类
的线
性分类
模型,输入为实例的特征向量,输出为实例的类别(取+1和-1)。感知机对应于输入空间中将
实例划分为两
类的分离超平面。
感知机旨在求出
该超
平面,
为求得超平面导入了基于误分类的损失函数
,利用
梯
度下降法对损失函数进行最优化
。
2 感知机模型
假设输入
空
间(
特征向量
)是x属于n维空间,
输出空间
为Y属于{-1,+1},输入X表示实例的特征向量,对应于输入空间的点,输出Y表示实例的类别,则由输入空间到输出空间的表达形式为:
f(x)=sign(w*x+b)
上面该函数称为感知机,其中w,b称为模型的参数,w
称为权值,b称为
偏
置,w*x表示为w,x的内积
这里
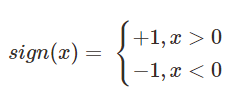
如果我们将sign称之为激活函数的话,感知机与logistic regression的差别就是感知机激活函数是sign,logistic regression的激活函数是sigmoid。
sign(x)将大于0的分为1,小于0的分为-1;sigmoid将大于0.5的分为1,小于0.5的分为0。因此sign又被称为单位阶跃函数,logistic regression也被看作是一种概率估计。(logistic后面会详细讲解)
该感知机线性方程表示为:w*x+b=0,它的几何意义如下图所示:
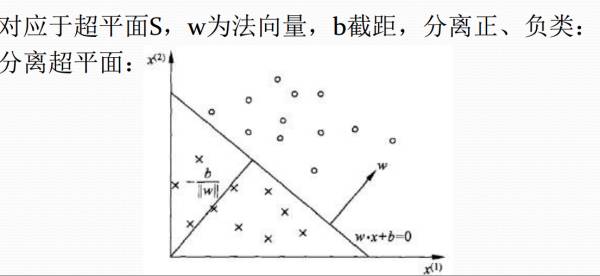
我们其实就
是
在学习
参数w与b,确定了w与b
,图上的直线(高维空间下为超平面)也就确定了,那么以后来一个数据点,我用训练好的模型进行预测判断,
如果大于0就分类到+1,如果小于0就分类到-1。
原文链接:
http://mp.weixin.qq.com/s/3V1DOrlW0UeH_b89i0HHpQ




